Sie sind hier: ICP » R. Hilfer » Publikationen

Appendix B Function Spaces

[page 61, §1]

[61.1.1] The set \mathbb{G} denotes an interval, a domain in \mathbb{R}^{d} or a measure space (\mathbb{G},\mathcal{A},\mu) [8] depending on the context. [61.1.2] \mathbb{K} stands for \mathbb{R} or \mathbb{C}. \gamma=(\gamma _{1},...,\gamma _{d})\in\mathbb{N}^{d}_{0} is a multiindex and |\gamma|=\sum _{{i=1}}^{d}\gamma _{i}. [61.1.3] For the definition of Hilbert and Banach spaces the reader may consult e.g. [128]. [61.1.4] The following notation is used for various spaces of continuous functions:

C^{{0}}(\mathbb{G}):=\{ f:\mathbb{G}\to\mathbb{K}|f\text{~is continuous}\} (B.1)
C^{{k}}(\mathbb{G}):=\{ f\in C^{{0}}(\mathbb{G})|f\text{~is $k$-times continuously differentiable}\} (B.2)
C_{{\mathrm{0}}}^{{k}}(\mathbb{G}):=\{ f\in C^{{k}}(\mathbb{G})|f\text{~vanishes at the boundary~}\partial\mathbb{G}\} (B.3)
C_{{\mathrm{b}}}^{{k}}(\mathbb{G}):=\{ f\in C^{{k}}(\mathbb{G})|f\text{~is bounded}\} (B.4)
C_{{\mathrm{c}}}^{{k}}(\mathbb{G}):=\{ f\in C^{{k}}(\mathbb{G})|f\text{~has compact support}\} (B.5)
C_{{\mathrm{ub}}}^{{k}}(\mathbb{G}):=\{ f\in C^{{k}}(\mathbb{G})|f\text{~is bounded and uniformly continuous}\} (B.6)
\mathrm{AC}^{{k}}([a,b]):=\{ f\in C^{{k}}([a,b])|f^{{(k)}}\text{~is absolutely continuous}\} (B.7)

[61.1.5] For compact \mathbb{G} the norm on these spaces is

\| f\| _{\infty}:=\sup _{{x\in\mathbb{G}}}|f(x)|. (B.8)

[61.1.6] The Lebesgue spaces over (\mathbb{G},\mathcal{A},\mu) are defined as

L^{{p}}_{{\mathrm{loc}}}(\mathbb{G},\mu):=\{ f:\mathbb{G}\to\mathbb{K}\;|\; f^{p}\text{~is integrable on every compact~}K\subset\mathbb{G}\} (B.9)
L^{{p}}(\mathbb{G},\mu):=\{ f:\mathbb{G}\to\mathbb{K}\;|\; f^{p}\text{~is integrable}\} (B.10)

with norm

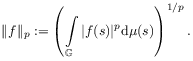\| f\| _{p}:=\left(\int\limits _{\mathbb{G}}|f(s)|^{p}\mathrm{d}\mu(s)\right)^{{1/p}}. (B.11)

[page 62, §0]    [62.0.1] For p=\infty

L^{{\infty}}(\mathbb{G},\mu):=\{ f:\mathbb{G}\to\mathbb{K}\;|\; f\text{~is measurable and~}\| f\| _{\infty}<\infty\} (B.12)

where

\| f\| _{\infty}:=\sup\left\{|z|:z\in f_{{\mathrm{ess}}}(\mathbb{G})\right\} (B.13)

and

f_{{\mathrm{ess}}}(\mathbb{G}):=\left\{ z\in\mathbb{C}:\mu\left(\{ x\in\mathbb{G}:|f(x)-z|<\varepsilon\}\right)\neq 0\text{~for all~}\varepsilon>0\right\} (B.14)

is the essential range of f.

[62.1.1] The Hölder spaces C^{{\alpha}}(\mathbb{G}) with 0<\alpha<1 are defined as

C^{{\alpha}}(\mathbb{G}):=\{ f:\mathbb{G}\to\mathbb{K}|\exists c\geq 0\text{~s.t.~}|f(x)-f(y)|\leq c|x-y|^{\alpha},\forall x,y\in\mathbb{G}\} (B.15)

with norm

\| f\| _{\alpha}:=\| f\| _{\infty}+c_{\alpha} (B.16)

where c_{\alpha} is the smallest constant c in (B.15). [62.1.2] For \alpha>1 the Hölder space C^{{\alpha}}(\mathbb{G}) contains only the constant functions and therefore \alpha is chosen as 0<\alpha<1. [62.1.3] The spaces C^{{k,\alpha}}(\mathbb{G}), k\in\mathbb{N}, consist of those functions f\in C^{{k}}(\mathbb{G}) whose partial derivatives of order k all belong to C^{{\alpha}}(\mathbb{G}).

[62.2.1] The Sobolev spaces are defined by

W^{{k,p}}(\mathbb{G})=\left\{ f\in L^{{p}}(\mathbb{G}):\parbox{136.573228pt}{\small$f${~is $k$-times differentiable in the sense of distributions and~}$\mathrm{D}^{\gamma}f\in L^{{p}}(\mathbb{G})$ ~for all $\gamma\in\mathbb{N}^{d}_{0}$ with $|\gamma|\leq k$ }\right\} (B.17)

where the derivative \mathrm{D}^{\gamma}=\partial _{1}^{{\gamma _{1}}}...\partial _{d}^{{\gamma _{d}}} with multiindex \gamma=(\gamma _{1},...,\gamma _{d})\in\mathbb{N}^{d}_{0} is understood in the sense of distributions. [62.2.2] A distribution f is in W^{{k,p}}(\mathbb{G}) if and only if for each \gamma\in\mathbb{N}^{d}_{0} with |\gamma|\leq k there exists f_{\gamma}\in L^{{p}}(\mathbb{G}) such that

\int\limits _{\mathbb{G}}\phi f_{\gamma}\mathrm{d}x=(-1)^{{|\gamma|}}\int\limits _{\mathbb{G}}(\mathrm{D}^{\gamma}\phi)f\mathrm{d}x (B.18)

for all test functions \phi. [62.2.3] In the special case d=1 one has f\in W^{{k,p}}(\mathbb{G}) if and only if f\in C^{{k-1}}(\mathbb{G}), f^{{(k-1)}}\in\mathrm{AC}(\mathbb{G}), and f^{{(j)}}\in L^{{p}}(\mathbb{G}) for j=0,1,...,k. [62.2.4] The Sobolev spaces are equipped with the norm

\| f\| _{{W^{{k,p}}(\mathbb{G})}}=\sum _{{|\gamma|\leq m}}\|\mathrm{D}^{\gamma}f\| _{p} (B.19)

(see [2]). [62.2.5] A function is called rapidly decreasing if it is infinitely many times differentiable, i.e. f\in C^{{\infty}}(\mathbb{R}^{d}) and

\lim _{{|x|\to\infty}}|x|^{n}\mathrm{D}^{\gamma}f(x)=0 (B.20)

[page 63, §0]    for all n\in\mathbb{N} and \gamma\in\mathbb{N}^{d}. [63.0.1] The test function space

\mathcal{S}{(\mathbb{R}^{d})}:=\{ f\in C^{{\infty}}(\mathbb{R}^{d})|f\text{~is rapidly decreasing}\} (B.21)

is called Schwartz space.