Appendix C Distributions

[page 65, §1]

[65.1.1] Distributions are generalized functions [31]. [65.1.2] They were invented to overcome the differentiability requirements for functions in analysis and mathematical physics [105, 63]. [65.1.3] Distribution theory has also a physical origin. [65.1.4] A physical observable $f$ can never be measured at a point $x\in\mathbb{R}^{d}$ because every measurement apparatus averages over a small volume around $x$ [115]. [65.1.5] This ‘‘smearing out’’ can be modelled as an integration with smooth ‘‘test functions’’ having compact support.

[65.2.1] Let $X$ denote the space of admissible test functions. [65.2.2] Commonly used test function spaces are $C^{{\infty}}(\mathbb{R}^{d})$ , the space of infinitely often differentiable functions, $C_{{\mathrm{c}}}^{{\infty}}(\mathbb{R}^{d})$ , the space of smooth functions with compact support (see (B.5)), $C_{{\mathrm{0}}}^{{\infty}}(\mathbb{R}^{d})$ , the space of smooth functions vanishing at infinity (see (B.3)), or the so called Schwartz space $\mathcal{S}{(\mathbb{R}^{d})}$ of smooth functions decreasing rapidly at infinity (see (B.21)).

[65.3.1] A distribution $\mathit{F}:X\to\mathbb{K}$ is a linear and continuous mapping that maps $\varphi\in X$ to a real ( $\mathbb{K}=\mathbb{R}$ ) or complex ( $\mathbb{K}=\mathbb{C}$ ) number ¹² (This is a footnote:) ¹²For vector valued distributions see [106]. [65.3.2] There exists a canonical correspondence between functions and distributions. [65.3.3] More precisely, for every locally integrable function $f\in L^{{1}}_{{\mathrm{loc}}}(\mathbb{R}^{d})$ there exists a distribution $\mathit{F}_{f}=\langle f,.\rangle$ (often also denoted with the same symbol $f$ ) defined by

$\mathit{F}_{f}(\varphi)=\langle f,\varphi\rangle=\int\limits _{{\mathbb{R}^{d}}}f(x)\varphi(x)\;\mathrm{d}x$

(C.1)

for every test function $\varphi\in X$ . [65.3.4] Distributions that can be written in this way are called regular distributions. [65.3.5] Distributions that are not regular are sometimes called singular. [65.3.6] The mapping $f\to\langle f,.\rangle$ that assigns to a locally integrable $f$ its associated distribution is injective and continuous. [65.3.7] The set of distributions is again a vector space, namely the dual space of the vector space of test functions, and it is denoted as $X^{\prime}$ where $X$ is the test function space.

[page 66, §1] [66.1.1] Important examples for singular distributions are the Dirac $\delta$ -function and its derivatives. [66.1.2] They are defined by the rules

	$\displaystyle\int\limits\delta(x)\varphi(x)\mathrm{d}x=\varphi(0)$		(C.2)
	$\displaystyle\int\limits\delta^{{(n)}}(x)\varphi(x)=(-1)^{n}\left.\frac{\mathrm{d}^{n}\varphi}{\mathrm{d}x^{n}}\right\|_{{x=0}}$		(C.3)

for every test function $\varphi\in X$ and $n\in\mathbb{N}$ . [66.1.3] Clearly, $\delta(x)$ is not a function, because if it were a function, then $\int\limits\delta(x)\varphi(x)\mathrm{d}x=0$ would have to hold. [66.1.4] Another example for a singular distribution is the finite part or principal value $\mathcal{P}\left\{ 1/x\right\}$ of $1/x$ . [66.1.5] It is defined by

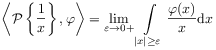$\left\langle\mathcal{P}\left\{\frac{1}{x}\right\},\varphi\right\rangle=\lim _{{\varepsilon\to 0+}}\int\limits _{{|x|\geq\varepsilon}}\frac{\varphi(x)}{x}\mathrm{d}x$

(C.4)

for $\varphi\in C_{{\mathrm{c}}}^{{\infty}}(\mathbb{R})$ . [66.1.6] It is a singular distribution on $\mathbb{R}$ , but regular on $\mathbb{R}\setminus\{ 0\}$ where it coincides with the function $1/x$ .

[66.2.1] Equation (C.2) illustrates how distributions circumvent the limitations of differentiation for ordinary functions. [66.2.2] The basic idea is the formula for partial integration

$\int\limits _{\mathbb{G}}\partial _{i}f(x)\varphi(x)\mathrm{d}x=-\int\limits _{\mathbb{G}}f(x)\partial _{i}\varphi(x)\mathrm{d}x$

(C.5)

valid for $f\in C_{{\mathrm{c}}}^{{1}}(\mathbb{G})$ , $\varphi\in C^{{1}}(\mathbb{G})$ , $i=1,...,d$ and $\mathbb{G}\subset\mathbb{R}^{d}$ an open set. [66.2.3] The formula is proved by extending $f\varphi$ as $0$ to all of $\mathbb{R}^{d}$ and using Leibniz’ product rule. [66.2.4] Rewriting the formula as

$\langle\partial _{i}f,\varphi\rangle=-\langle f,\partial _{i}\varphi\rangle$

(C.6)

suggests to view $\partial _{i}f$ again as a linear continuous mapping (integral) on a space $X$ of test functions $\varphi\in X$ . [66.2.5] Then the formula is a rule for differentiating $f$ given that $\varphi$ is differentiable.

[66.3.1] Distributions on the test function space $\mathcal{S}{(\mathbb{R}^{d})}$ are called tempered distributions. [66.3.2] The space of tempered distributions is the dual space $\mathcal{S}{(\mathbb{R}^{d})}^{\prime}$ . [66.3.3] Tempered distributions generalize locally integrable functions growing at most polynomially for $|x|\to\infty$ . [66.3.4] All distributions with compact support are tempered. Square integrable functions are tempered distributions. [66.3.5] The derivative of a tempered distribution is again a tempered distribution. [66.3.6] $\mathcal{S}{(\mathbb{R}^{d})}$ is dense in $L^{{p}}(\mathbb{R}^{d})$ for all $1\leq p<\infty$ but not in $L^{{\infty}}(\mathbb{R}^{d})$ . [66.3.7] The Fourier transform and its inverse are continous maps of the Schwartz space onto itself. [66.3.8] A distribution $f$ belongs to $\mathcal{S}{(\mathbb{R}^{d})}^{\prime}$ if and only if it is the derivative of a continuous function with slow growth, i.e. it is of the form $f=\mathrm{D}^{\gamma}[(1+|x|^{2})^{{k/2}}g(x)]$

[page 67, §0] where $k\in\mathbb{N}$ , $\gamma\in\mathbb{N}^{d}$ and $g$ is a bounded continuous function on $\mathbb{R}^{d}$ . [67.0.1] Note that the exponential function is not a tempered distribution.

[67.1.1] A distribution $f\in\mathcal{S}{(\mathbb{R}^{d})}^{\prime}$ is said to have compact support if there exists a compact subset $K\subset\mathbb{R}^{d}$ such that $\langle f,\varphi\rangle=0$ for all test functions with $\mathrm{supp}\,\varphi\cap K=\emptyset$ . [67.1.2] The Dirac $\delta$ -function is an example. [67.1.3] Other examples are Radon measures on a compact set $K$ . [67.1.4] They can be described as linear functionals on $C^{{0}}(K)$ . [67.1.5] If the set $K$ is sufficiently regular (e.g. if it is the closure of a region with piecewise smooth boundary) then every distribution with compact support in $K$ can be written in the form

$f=\sum _{{|\gamma|\leq N}}\mathrm{D}^{\gamma}f_{\gamma}$

(C.7)

where $\gamma=(\gamma _{1},...,\gamma _{d})$ , $\gamma _{j}\geq 0$ is a multiindex, $|\gamma|=\sum\gamma _{i}$ and $f_{\gamma}$ are continuous functions of compact support. [67.1.6] Here $N\geq 0$ and the partial derivatives in $\mathrm{D}^{\gamma}$ are distributional derivatives defined above. [67.1.7] A special case are distributions with support in a single point taken as $\{ 0\}$ . [67.1.8] Any such distributions can be written in the form

$f=\sum _{{|\gamma|\leq N}}c_{\gamma}\mathrm{D}^{\gamma}\delta$

(C.8)

where $\delta$ is the Dirac $\delta$ -function and $c_{\gamma}$ are constants.

[67.2.1] The multiplication of a distribution $f$ with a smooth function $g$ is defined by the formula $\langle gf,\varphi\rangle=\langle f,g\varphi\rangle$ where $g\in C^{{\infty}}(\mathbb{G})$ . [67.2.2] A combination of multiplication by a smooth function and differentiation allows to define differential operators

$A=\sum _{{|\gamma|\leq m}}a_{\gamma}(x)\mathrm{D}^{\gamma}$

(C.9)

with smooth $a_{\gamma}(x)\in C^{{\infty}}(\mathbb{G})$ . [67.2.3] They are well defined for all distributions in $C_{{\mathrm{c}}}^{{\infty}}(\mathbb{G})^{\prime}$ .

[67.3.1] A distribution is called homogeneous of degree $\alpha\in\mathbb{C}$ if

$f(\lambda x)=\lambda^{\alpha}f(x)$

(C.10)

for all $\lambda>0$ . [67.3.2] Here $\lambda^{\alpha}=\exp(\alpha\log\lambda)$ is the standard definition. [67.3.3] The Dirac $\delta$ -distribution is homogeneous of degree $-d$ . [67.3.4] For regular distributions the definition coincides with homogeneity of functions $f\in L^{{1}}_{{\mathrm{loc}}}(\mathbb{R}^{d})$ . [67.3.5] The convolution kernels $K_{\pm}^{\alpha}$ from eq. (2.39) are homogeneous of degree $\alpha-1$ . [67.3.6] Homogeneous distributions remain homogeneous under differentiation. [67.3.7] A homogeneous locally integrable function $g$ on $\mathbb{R}^{d}\setminus\{ 0\}$ of degree $\alpha$ can be extended to homogeneous distributions $f$ on all of $\mathbb{R}^{d}$ . [67.3.8] The degree of homogeneity of $f$ must again be $\alpha$ . [67.3.9] As long as $\alpha\neq-d,-d-1,-d-2,...$ the integral

$\langle g_{\beta},\varphi\rangle=\int\limits g\left(\frac{x}{|x|}\right)|x|^{\beta}\mathrm{d}^{d}x$

(C.11)

[page 68, §0] which converges absolutely for $\mathrm{Re}\,\beta>-d$ can be used to define $f=g_{\alpha}$ by analytic continuation from the region $\mathrm{Re}\,\beta>-d$ to the point $\alpha$ . [68.0.1] For $\alpha=-d,-d-1,...$ , however, this is not always possible. [68.0.2] An example is the function $1/|x|$ on $\mathbb{R}\setminus\{ 0\}$ . [68.0.3] It cannot be extended to a homogeneous distribution of degree $-1$ on all of $\mathbb{R}$ .

[68.1.1] For $f\in L^{{1}}_{{\mathrm{loc}}}(\mathbb{G}_{1})$ and $g\in L^{{1}}_{{\mathrm{loc}}}(\mathbb{G}_{2})$ their tensor product is the function $(f\otimes g)(x,y)=f(x)g(y)$ defined on $\mathbb{G}_{1}\times\mathbb{G}_{2}$ . [68.1.2] The function $f\otimes g$ gives a functional

$\langle f\otimes g,\varphi(x,y)\rangle=\langle f(x),\langle g(y),\varphi(x,y)\rangle\rangle$

(C.12)

for $\varphi\in C_{{\mathrm{c}}}^{{\infty}}(\mathbb{G}_{1}\times\mathbb{G}_{2})$ . [68.1.3] For two distributions this formula defines the their tensor product. [68.1.4] An example is a measure $\mu(x)\otimes\delta(y)$ concentrated on the surface $y=0$ in $\mathbb{G}_{1}\otimes\mathbb{G}_{2}$ where $\mu(x)$ is a measure on $\mathbb{G}_{1}$ . [68.1.5] The convolution of distribution defined in the main text (see eq. (2.52) can then be defined by the formula

$\langle f*g,\varphi\rangle=\langle(f\otimes g)(x,y),\varphi(x+y)\rangle$

(C.13)

whenever one of the distributions $f$ or $g$ has compact support.

Author:	R. Hilfer
also published in:	Anomalous Transport: Foundations and Applications, Wiley-VCH, Weinheim, page 17-73 (2008), ISBN: 978-3-527-40722-4 Copyright © 2007 R. Hilfer, Stuttgart
first published on:	June 6th, 2007