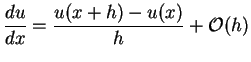Next: Potenzreihenentwicklung
Up: Numerische Lösungsverfahren
Previous: Numerische Lösungsverfahren
Die generelle Methode besteht nun darin, das Intervall ![$ [0,x]$](img494.gif) in
in 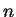 Stützpunkte
Stützpunkte
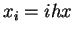 |
(5.37) |
mit
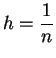 |
(5.38) |
aufzuteilen, an welchen 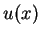 bestimmt werden soll.
Definiere
bestimmt werden soll.
Definiere
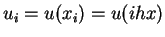 |
(5.39) |
für
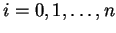 .
.
Dann ist das Ziel, eine Form für
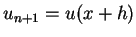 zu finden,
welche von den
zu finden,
welche von den 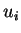 mit
mit 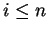 abhängt und so
abhängt und so
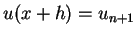 rekursiv aus den links davon liegenden Punkten zu bestimmen.
Die zu lösende Gleichung ist Gl. (
rekursiv aus den links davon liegenden Punkten zu bestimmen.
Die zu lösende Gleichung ist Gl. (![[*]](file:/mnt/bison/local/lib/latex2html/icons/crossref.gif) )
)
Beim Euler-Verfahren ersetzt man den Differentialquotienten
durch den Differenzquotienten.
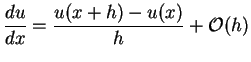 |
(5.40) |
und erhält die Rekursion
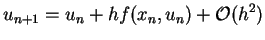 |
(5.41) |
Dies ist die Euler-Methode. Sie wird in der Praxis kaum benutzt,
da sie zu ungenau ist.




Next: Potenzreihenentwicklung
Up: Numerische Lösungsverfahren
Previous: Numerische Lösungsverfahren
© R.Hilfer et al., ICA-1, Univ. Stuttgart
28.6.2002
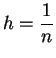
![]() zu finden,
welche von den
zu finden,
welche von den ![]() mit
mit ![]() abhängt und so
abhängt und so
![]() rekursiv aus den links davon liegenden Punkten zu bestimmen.
Die zu lösende Gleichung ist Gl. (
rekursiv aus den links davon liegenden Punkten zu bestimmen.
Die zu lösende Gleichung ist Gl. (![]() )
)