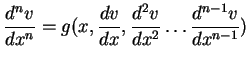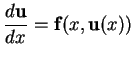Next: Numerische Lösungsverfahren
Up: Gewöhnliche Differentialgleichungen
Previous: Das ebene mathematische Pendel
Die Trommelfellgleichung und das ebene Pendel hatten die Form
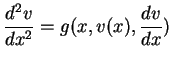 |
(5.33) |
mit Anfangsbedingungen
Dabei lauten die Entsprechungen
Trommelfell:
 |
Auslenkung |
 |
Zeit |
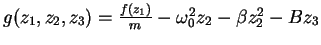
Pendel:
 |
Auslenkungswinkel |
 |
Zeit |
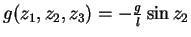
Definiert man nun die Größen
so geht (![[*]](file:/mnt/bison/local/lib/latex2html/icons/crossref.gif) ) über in das Gleichungssystem von
Differentialgleichungen 1. Ordnung.
) über in das Gleichungssystem von
Differentialgleichungen 1. Ordnung.
mit Anfangsbedingungen
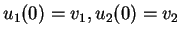
in Vektorschreibweise mit
wird daraus
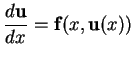 |
(5.34) |
mit Anfangsbedingung
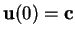 .
.
Analog läßt sich eine Gleichung 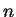 -ter Ordnung
-ter Ordnung
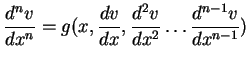 |
(5.35) |
in ein System von Gleichungen 1. Ordnung
umwandeln. Deshalb wird im Folgenden nur noch eine Gleichung 1.
Ordnung betrachtet.
Im einfachsten Fall ist also die Gleichung
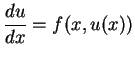 |
(5.36) |
zu lösen.




Next: Numerische Lösungsverfahren
Up: Gewöhnliche Differentialgleichungen
Previous: Das ebene mathematische Pendel
© R.Hilfer et al., ICA-1, Univ. Stuttgart
28.6.2002
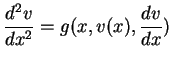
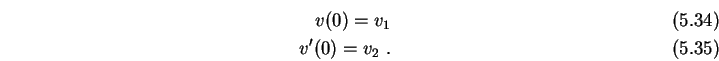
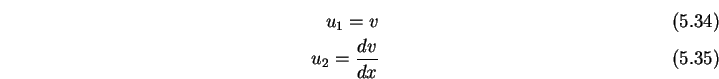
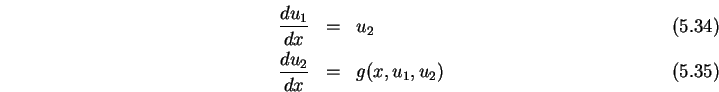
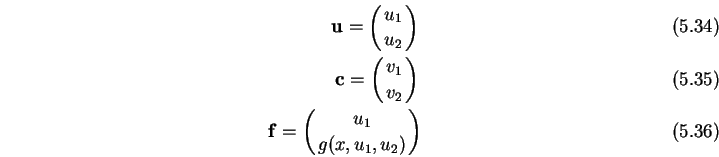
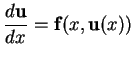
![]() -ter Ordnung
-ter Ordnung