Verlet-Methode

Schreibt man () für $-h$ statt $h$ so gilt auch

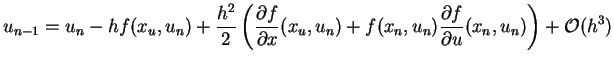$$u_{n-1}= u_n-hf(x_u,u_n)+ \frac{h^2}{2}\left(\frac{\partial f}{\p... ...x_u,u_n)+f(x_n,u_n) \frac{\partial f}{\partial u}(x_n,u_n)\right)+{\cal O}(h^3)$$ (5.45)

Addiert man dies auf () so folgt

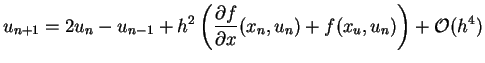$$u_{n+1}= 2 u_n-u_{n-1}+ h^2\left(\frac{\partial f}{\partial x}(x_n,u_n)+f(x_u,u_n)\right)+ {\cal O}(h^4)$$ (5.46)

Dieser Ausdruck ist von höherer Ordnung, da die ungeraden Potenzen von $h$ herausfallen. Allerdings braucht man jetzt jeweils $2$ vorhergehende Werte und somit auch zwei Startwerte.

Dazu kann man $u_0=u(0)$ und $u_0'=\frac{u_0-u(-h)}{h}$ benutzen, falls $u(-h)$ bekannt ist. Sonst setzt man einfach $u_0'=0$, i.e. $u(-h)=u_0$.