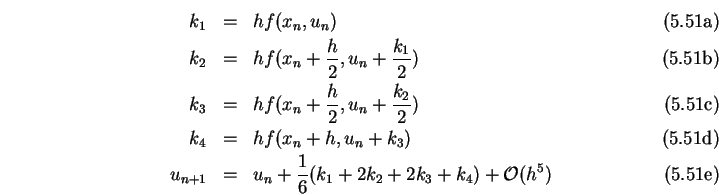Hierbei handelt es sich um eine ganze Klasse von Methoden. Wir zeigen, wie man ein Verfahren zweiter Ordnung gewinnt, und zitieren dann die Formel für einige häufig benutzte Verfahren.
Die Idee basiert auf der allgemeinen und exakten Bezeichnung, die man
durch Integration von (![]() ) über
) über
![]() erhält.
erhält.
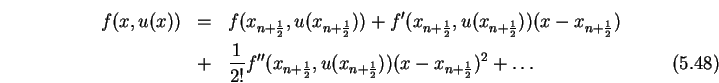
![\begin{eqnarray}u_{n+1}&=&u_n+(x_{n+1}-x_n)f(x_{n+\frac{1}{2}},u_{n+\frac{1}{2}}...
...1}{2}})
[(x_{n+1}-x_{n+\frac{1}{2}})^2-(x_n-x_{n+\frac{1}{2}})^2]
\end{eqnarray}](img524.gif)
| (5.48) |
Nun ist natürlich
![]() unbekannt.
Da aber der Fehler
unbekannt.
Da aber der Fehler
![]() ist, reicht es aus
ist, reicht es aus
![]() als
als
![]() zu approximieren wobei
zu approximieren wobei ![]() aus einer Methode stammt, die z.B. nur
aus einer Methode stammt, die z.B. nur
![]() ist. Also z.B. die
Euler-Methode.
ist. Also z.B. die
Euler-Methode.
| (5.49) |
Dies ist die generelle Idee des Runge-Kutta-Verfahren, dass man
das Intervall in (![]() ) approximiert und an den
Zwischenstellen einfache Approximationen von
) approximiert und an den
Zwischenstellen einfache Approximationen von ![]() anstatt d. exakten
Werte benutzt. Insgesamt haben wir also folgendes Verfahren aus
zwei Schritten.
anstatt d. exakten
Werte benutzt. Insgesamt haben wir also folgendes Verfahren aus
zwei Schritten.
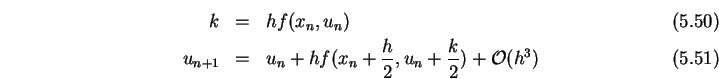
Vorteile:
Runge-Kutta-Verfahren höherer Ordnung erhält man, indem man andere
Quadraturformeln für das Integral in Gleichung (![]() )
benutzt. Benutzt man die Simpsonregel in (
)
benutzt. Benutzt man die Simpsonregel in (![]() ) so hat man
) so hat man
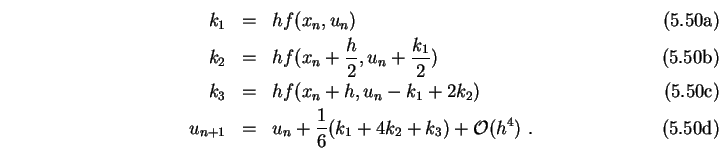
Er erfordert, dass ![]() dreimal ausgerechnet wird. Die Erfahrung hat
gezeigt, dass ein RK-Verfahren 4. Ordnung einerseits genau ist
und andererseits wenig Rechenaufwand erfordert. Der am häufigsten
verwendete Algorithmus lautet
dreimal ausgerechnet wird. Die Erfahrung hat
gezeigt, dass ein RK-Verfahren 4. Ordnung einerseits genau ist
und andererseits wenig Rechenaufwand erfordert. Der am häufigsten
verwendete Algorithmus lautet