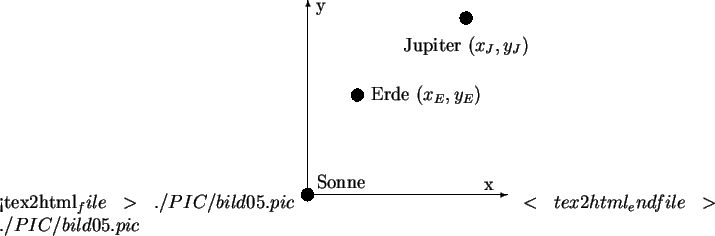
 |
Kommt zu den Körpern Sonne und Erde noch ein dritter (beispielsweise
der Jupiter) hinzu, so ist dieses Problem nicht mehr analytisch lösbar. Die
Keplerschen Gesetze zur Planetenbewegung gelten nicht mehr. Allgemein ist
das beim ![]() -Körperproblem (
-Körperproblem (![]() ) so. Numerisch läßt sich dieses
Problem immer noch lösen. Wir benötigen
als erstes das Gravitationsgesetz für Erde-Jupiter:
) so. Numerisch läßt sich dieses
Problem immer noch lösen. Wir benötigen
als erstes das Gravitationsgesetz für Erde-Jupiter:
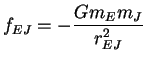 mit mit |
(5.72) |
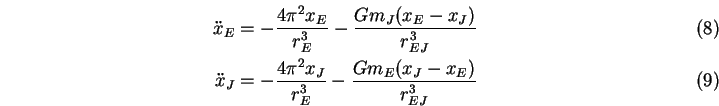
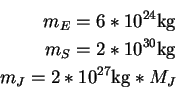
Den Faktor ![]() benutzen wir später in der Simulation um auszuprobieren,
wie sich unser System verhalten würde, wenn die Masse des Jupiters
geändert würde.
Der Radius der Jupiterbahn ist
benutzen wir später in der Simulation um auszuprobieren,
wie sich unser System verhalten würde, wenn die Masse des Jupiters
geändert würde.
Der Radius der Jupiterbahn ist ![]() AE und seine
Bahngeschwindigkeit ist
AE und seine
Bahngeschwindigkeit ist ![]() AE/a. Man kann nun die Konstanten
AE/a. Man kann nun die Konstanten
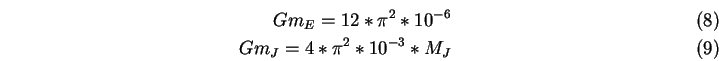
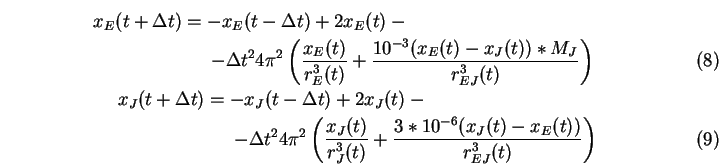
double p0x, p1x, p2x, dp1x, t;
double p0y, p1y, p2y, dp1y, r3e;
double q0x, q1x, q2x, dq1x, r3j;
double q0y, q1y, q2y, dq1y, r3ej;
double alpha, massj, t_max, dt;
// ...
// loop from t=0 to t=t_max
t=0.0;
ofstream outfile("orbit.dat");
for( int i=0; i<t_max/dt; i++ ) {
r3e=1./pow(p1x*p1x+p1y*p1y,beta);
r3j=1./pow(q1x*q1x+q1y*q1y,beta);
r3ej=1./pow((p1x-q1x)*(p1x-q1x)+(p1y-q1y)*(p1y-q1y),beta);
// Verlet sums
p2x=2.*p1x-p0x-pi24*dt2*
(r3e*p1x+r3ej*1.e-3*massj*(p1x-q1x)); // Earth
p2y=2.*p1y-p0y-pi24*dt2*
(r3e*p1y+r3ej*1.e-3*massj*(p1y-q1y));
q2x=2.*q1x-q0x-pi24*dt2*
(r3j*q1x-r3ej*3.e-6*(p1x-q1x)); // Jupiter
q2y=2.*q1y-q0y-pi24*dt2*
(r3j*q1y-r3ej*3.e-6*(p1y-q1y));
outfile << t << ' ' << p1x << ' ' << p1y <<
' ' << q1x << ' ' << q1y << '\n';
t=t+dt;
p0x=p1x; // change new->old
p0y=p1y;
p1x=p2x;
p1y=p2y;
q0x=q1x; // change new->old
q0y=q1y;
q1x=q2x;
q1y=q2y;
}
Modifizieren Sie die Parameter, um zu sehen, daß sehr haeufig
chaotische Trajektorien entstehen. Ebenso ist
das allgemeine ![]() -Körper-Problem chaotisch!
-Körper-Problem chaotisch!