 |
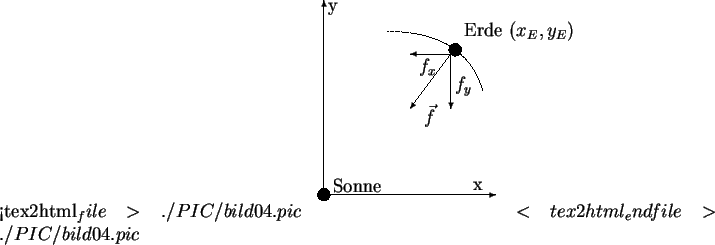
Im Folgenden betrachten wir die Berechnung der Planetenbewegung, zunächst
einmal der Erde, um die Sonne. Entscheidend hierbei ist die Gravitationskraft
zwischen der Masse der Sonne (![]() ) und der Masse der Erde (
) und der Masse der Erde (![]() ).
Die Formel für diese Kraft lautet :
).
Die Formel für diese Kraft lautet :
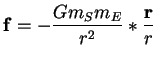 |
(5.66) |
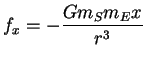 , , 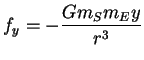 und und |
(5.67) |
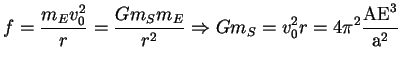 |
(5.68) |
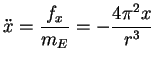 und und 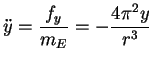 |
(5.69) |
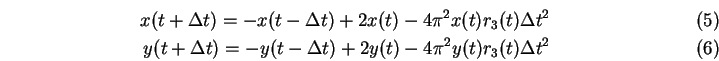
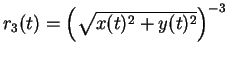 verwendet worden.
verwendet worden.
int main()
{
double p0x, p1x, p2x, dp0x, dp1x, dp2x, t;
double p0y, p1y, p2y, dp0y, dp1y, dp2y, r3;
double alpha, t_max, dt;
// read parameters
cout << "Anf.x "; cin >> p1x;
cout << "Anf.y "; cin >> p1y;
cout << "Anf.vx "; cin >> dp1x;
cout << "Anf.vy "; cin >> dp1y;
cout << "Alpha "; cin >> alpha;
cout << "Gesamtzeit "; cin >> t_max;
cout << "Zeitintervall "; cin >> dt;
const double beta=(alpha)/2.;
const double dt2=dt*dt;
const double pi24=4.*M_PI*M_PI;
// setup initial conditions
p0x=p1x-dt*dp1x;
p0y=p1y-dt*dp1y;
dp0x=dp1x;
dp0y=dp1y;
// loop from t=0 to t=t_max
t=0.0;
ofstream outfile("orbit.dat");
for( int i=0; i<t_max/dt; i++ ) {
r3=1./pow(p1x*p1x+p1y*p1y,beta);
p2x=2.*p1x-p0x-pi24*dt2*r3*p1x; // Verlet algorithm
p2y=2.*p1y-p0y-pi24*dt2*r3*p1y;
outfile << t << ' ' << p1x << ' ' << p1y << '\n';
t=t+dt;
p0x=p1x; // change new->old
p0y=p1y;
p1x=p2x;
p1y=p2y;
}
outfile.close();
}
Für ideale Anfangsbedingungen, das wäre ![]() ,
, ![]() ,
, ![]() und
und
![]() , erhält man für die Erdbewegung eine Kreisbahn, siehe Abbildung
, erhält man für die Erdbewegung eine Kreisbahn, siehe Abbildung
![]() (links). Verändert man die Anfangsgeschwindigkeit
auf
(links). Verändert man die Anfangsgeschwindigkeit
auf ![]() , so ergibt sich eine elliptische Bahn (rechts).
, so ergibt sich eine elliptische Bahn (rechts).
Eine weitere Variationsmöglichkeit besteht in der Änderung des
Gravitationsgesetzes. Anstatt die Gravitationskraft proportional zu
![]() abfallen zu lassen, kann man sie auch proportional zu
abfallen zu lassen, kann man sie auch proportional zu
![]() machen. Allgemein wird im obigen
Programm
machen. Allgemein wird im obigen
Programm r=1/sqrt(pow(r, alpha)) verwendet,
wobei pow(r, alpha) der Potenzierung ![]() entspricht.
Abbildung
entspricht.
Abbildung ![]() zeigt vier verschiedene Beispiele mit
Werten für
zeigt vier verschiedene Beispiele mit
Werten für ![]() zwischen
zwischen ![]() und
und ![]() , wobei
, wobei
![]() .
Die Rotation der Ellipse bei den Beispielen für
.
Die Rotation der Ellipse bei den Beispielen für
![]() nennt man Präzession.
nennt man Präzession.
Für
![]() fällt auf, daß die Erde, nachdem sie in die Nähe der
Sonne ``geflogen'' ist, sich mit hoher Geschwindigkeit aus dem System entfernt.
Dies ist allerdings ein numerisches Problem.
Für diesen Effekt ist die Wahl eines zu großen
fällt auf, daß die Erde, nachdem sie in die Nähe der
Sonne ``geflogen'' ist, sich mit hoher Geschwindigkeit aus dem System entfernt.
Dies ist allerdings ein numerisches Problem.
Für diesen Effekt ist die Wahl eines zu großen ![]() verantwortlich,
daß bei großen Geschwindigkeitsänderungen kleiner sein sollte.
Allerdings würde bei einem kleineren
verantwortlich,
daß bei großen Geschwindigkeitsänderungen kleiner sein sollte.
Allerdings würde bei einem kleineren ![]() die Simulation zu lange
dauern. Man benötigt also ein automatisches Verfahren, das die Größe von
die Simulation zu lange
dauern. Man benötigt also ein automatisches Verfahren, das die Größe von
![]() regelt. Eine Möglichkeit ist es, die Änderung der Energie für
verschiedene
regelt. Eine Möglichkeit ist es, die Änderung der Energie für
verschiedene ![]() zu vergleichen und den Zeitschritt dementsprechend
zu verändern (adaptives Verfahren). Dazu bietet sich z.B. das Runge-Kutta
Verfahren an, da dort sowieso Werte zur Zeit
zu vergleichen und den Zeitschritt dementsprechend
zu verändern (adaptives Verfahren). Dazu bietet sich z.B. das Runge-Kutta
Verfahren an, da dort sowieso Werte zur Zeit
![]() berechnet
werden. Die Energie der Erde ist
berechnet
werden. Die Energie der Erde ist
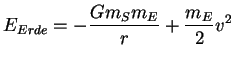 |
(5.70) |
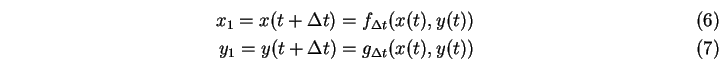
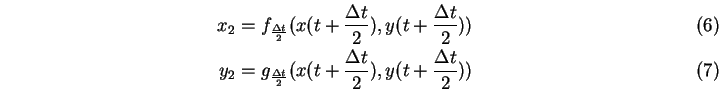
| (5.71) |