Den Unterschied zwischen Gesetzen und Modellen
kann man sich bereits am Beispiel des Federpendels
vor Augen führen.
Die Beobachtung zeigt, daß die Auslenkung ![]() des
Federpendels eine periodisch wiederkehrende Funktion ist.
Eine mathematische Modellierung der Bewegung wäre deshalb
durch eine periodische Funktion möglich.
Es sei
des
Federpendels eine periodisch wiederkehrende Funktion ist.
Eine mathematische Modellierung der Bewegung wäre deshalb
durch eine periodische Funktion möglich.
Es sei ![]() die Periode des Oszillators.
Dann wäre eine Sägezahnschwingung
die Periode des Oszillators.
Dann wäre eine Sägezahnschwingung
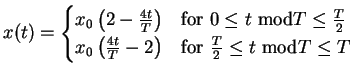 |
(1.1) |
| (1.2) |
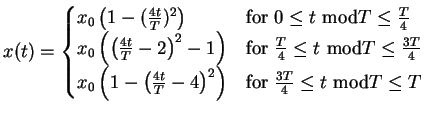 |
(1.3) |
Eine solche Modellierung ist jedoch unbefriedigend,
obwohl sie in der Praxis sehr häufig vorkommt.
Es gibt eine unendliche Vielfalt von periodischen
Funktionen, und jede dieser Funktionen hat mehrere
Parameter (etwa ![]() ).
In der Praxis geht man so vor, daß man aus
der unendlichen Vielfalt der Möglichkeiten
einige wenige auswählt, und dann die Parameter
der gewählten Funktionen (hier
).
In der Praxis geht man so vor, daß man aus
der unendlichen Vielfalt der Möglichkeiten
einige wenige auswählt, und dann die Parameter
der gewählten Funktionen (hier ![]() ) solange
an experimentelle Daten anpasst, bis ein Modell
möglichst gut mit den Daten übereinstimmt.
Dieses Vorgehen kann nur glücken, wenn sich
das korrekte Modell zufällig in der Auswahl
befindet.
Die Wahrscheinlichkeit aus unendlich vielen Möglichkeiten
das wahre Modell zufällig auszuwählen ist Null.
Das Auffinden der korrekten Modellierung wäre
also reiner Zufall.
Dementsprechend häufig gibt es Abweichungen bei der
Vorhersage neuer experimenteller Daten mit einem solchen
Modell.
) solange
an experimentelle Daten anpasst, bis ein Modell
möglichst gut mit den Daten übereinstimmt.
Dieses Vorgehen kann nur glücken, wenn sich
das korrekte Modell zufällig in der Auswahl
befindet.
Die Wahrscheinlichkeit aus unendlich vielen Möglichkeiten
das wahre Modell zufällig auszuwählen ist Null.
Das Auffinden der korrekten Modellierung wäre
also reiner Zufall.
Dementsprechend häufig gibt es Abweichungen bei der
Vorhersage neuer experimenteller Daten mit einem solchen
Modell.
Die Gesetze der Physik schränken die Vielfalt der
Modelle ein und geben allgemeine Richtlinien
und Anleitungen zum Auffinden der korrekten
mathematischen Modellierung der experimentellen
Wirklichkeit.
Ausserdem geben sie den reinen Fitparametern der
mathematischen Modelle eine physikalische Interpretation.
Für das Federpendel sind die allgemeinen
Gesetze der Mechanik relevant.
Newtons zweites Gesetz postuliert die Proportionalität
der Kraft ![]() mit der Änderung der Bewegungsgröße
(Impuls)
mit der Änderung der Bewegungsgröße
(Impuls) ![]() nicht nur für ein Federpendel sondern für
ausnahmslos alle mechanischen Vorgänge.
Mathematisch formuliert lautet es
nicht nur für ein Federpendel sondern für
ausnahmslos alle mechanischen Vorgänge.
Mathematisch formuliert lautet es
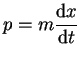 |
(1.5) |