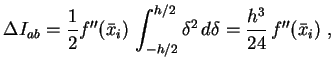Next: Die Trapezregel
Up: Integration
Previous: Integration
Die Aufgabe besteht darin ein bestimmtes Integral
numerisch zu berechnen.
Im Folgenden sei der Integrationsbereich von 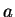 bis
bis 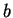 in
in 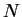 Intervalle mit Randpunkten
Intervalle mit Randpunkten
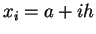 (
(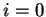 , ...,
, ..., 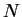 ),
und Breite
),
und Breite
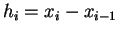 unterteilt.
Weiterhin bedeutet die Schreibweise
unterteilt.
Weiterhin bedeutet die Schreibweise
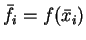 eine
Funktionsauswertung am Punkt
eine
Funktionsauswertung am Punkt
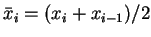 , in der
Mitte des Intervalls zwischen
, in der
Mitte des Intervalls zwischen 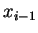 und
und 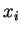 ,
sofern die analytische Form von
,
sofern die analytische Form von 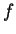 bekannt ist. Diese Situation
ist in Abb.
bekannt ist. Diese Situation
ist in Abb. ![[*]](file:/mnt/bison/local/lib/latex2html/icons/crossref.gif) zu sehen.
zu sehen.
Abbildung:
Schematische Darstellung eines Intervalls, dessen
Fläche nach der Mittelpunktsregel durch den Funktionswert
im Zentrum des Intervalls approximiert wird.
|
|
Damit ist 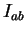 im Fall gleichgroßer Intervalle:
im Fall gleichgroßer Intervalle:
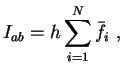 |
(4.13) |
mit
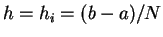 ,
oder bei allgemeinen Intervall-Längen:
,
oder bei allgemeinen Intervall-Längen:
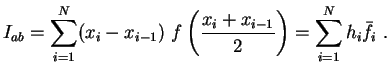 |
(4.14) |
Der Fehler einer Integration ist somit die Differenz zwischen der exakten
und der genäherten Lösung:
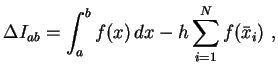 |
(4.15) |
wie sich durch Taylorentwicklung von 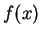 in kleinem Abstand
in kleinem Abstand 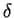 um
um 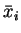 :
:
zeigen läßt. Setzt man Glg. (![[*]](file:/mnt/bison/local/lib/latex2html/icons/crossref.gif) ) in Glg. (
) in Glg. (![[*]](file:/mnt/bison/local/lib/latex2html/icons/crossref.gif) ) ein
und integriert, jeweils für ein Intervall, von
) ein
und integriert, jeweils für ein Intervall, von 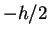 bis
bis 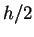 über
über 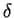 , so
sieht man, daß der erste Summand der Taylorreihe mit der Summe in Gleichung
(
, so
sieht man, daß der erste Summand der Taylorreihe mit der Summe in Gleichung
(![[*]](file:/mnt/bison/local/lib/latex2html/icons/crossref.gif) ) identisch ist.
Der zweite Summand verschwindet, da bei symmetrischer Integration eine zu
) identisch ist.
Der zweite Summand verschwindet, da bei symmetrischer Integration eine zu 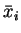 symmetrische Funktion (hier: alle
symmetrische Funktion (hier: alle 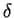 mit ungerader Potenz) verschwindet.
Damit errechnet sich der Fehler aus Glg. (
mit ungerader Potenz) verschwindet.
Damit errechnet sich der Fehler aus Glg. (![[*]](file:/mnt/bison/local/lib/latex2html/icons/crossref.gif) ) zu:
) zu:
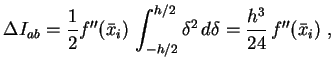 |
(4.16) |
d.h. der Fehler der Mittelpunktsregel ist von 3. Ordnung in 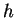 .
.




Next: Die Trapezregel
Up: Integration
Previous: Integration
© R.Hilfer et al., ICA-1, Univ. Stuttgart
28.6.2002
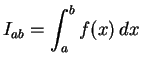
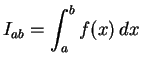
![\includegraphics[width=7cm]{FIGS/midpoint.eps}](img269.gif)
![]() im Fall gleichgroßer Intervalle:
im Fall gleichgroßer Intervalle: