Die Idee der Gauß-Quadratur besteht nun darin, nicht nur die
Gewichte ![]() optimal zu wählen, sondern auch die Stützstellen
optimal so zu wählen, dass Polynome exakt integriert werden. Genauer
gesagt werden sie so gewählt, dass Polynome und eine
Gewichtsfunktion
optimal zu wählen, sondern auch die Stützstellen
optimal so zu wählen, dass Polynome exakt integriert werden. Genauer
gesagt werden sie so gewählt, dass Polynome und eine
Gewichtsfunktion ![]() exakt integriert werden. Dies macht die
Gauß-Quadratur immer dann zur optimalen Methode, wenn der
Integrand modulo Gewichtsfunktion ,,sehr schön glatt'' ist. Sehr
schön glatt bedeutet dabei, dass er gut durch ein Polynom
approximierbar ist. Die Gewichtsfunktion kann dazu dienen,
integrierbare Singularitäten aus dem Integral zu entfernen.
exakt integriert werden. Dies macht die
Gauß-Quadratur immer dann zur optimalen Methode, wenn der
Integrand modulo Gewichtsfunktion ,,sehr schön glatt'' ist. Sehr
schön glatt bedeutet dabei, dass er gut durch ein Polynom
approximierbar ist. Die Gewichtsfunktion kann dazu dienen,
integrierbare Singularitäten aus dem Integral zu entfernen.
Sei also eine Gewichtsfunktion
![]() und eine ganze Zahl
und eine ganze Zahl ![]() gegeben. Dann besteht die Aufgabe darin, Gewichte
gegeben. Dann besteht die Aufgabe darin, Gewichte ![]() und
Stützstellen
und
Stützstellen ![]() zu finden, so dass die Näherung
zu finden, so dass die Näherung
Bemerkung: Wenn
![]() ist, reicht es aus das
Intervall
ist, reicht es aus das
Intervall
![]() zu betrachten, denn die Substitution
zu betrachten, denn die Substitution
![]() ,
,
![]()
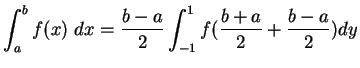 |
(4.40) |
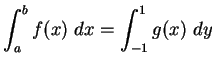 |
(4.41) |
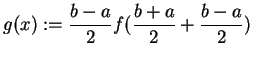 |
(4.42) |
Einfachstes Beispiel:
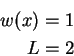
Dann ist
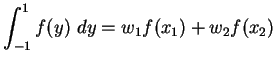 |
(4.43) |
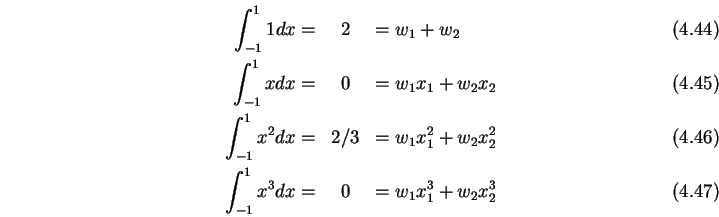
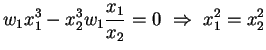 |
(4.44) |
| (4.45) |
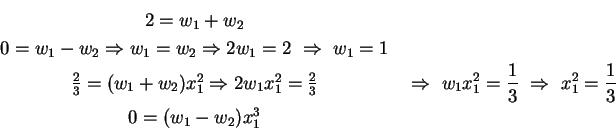
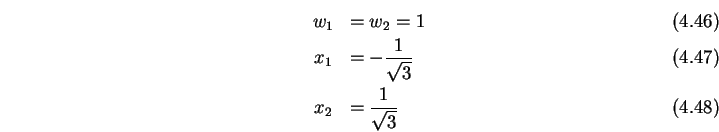
Mann kann nun Tabellen der ![]() und
und ![]() finden und damit die
Gaussche Quadratur anwenden.
finden und damit die
Gaussche Quadratur anwenden.
|
|
||
|
|
||
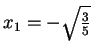 |
|
|
|
|
||
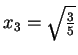 |
|
|
|
|
|
|
|
|
|