Wie bestimmt man die Stützstellen
In diesem Abschnitt geht es um die Frage:
Wie bestimmt man die Stützstellen ![]() und die
Gewichte
und die
Gewichte ![]() im allgemeinen?
im allgemeinen?
Die ursprüngliche Antwort von Gauss basiert auf Kettenbrüchen. Später gewann Jacobi(1826) die Ergebnisse von Gauß mit Hilfe von orthogonalen Polynomen. Christoffel (1877) behandelte beliebige Gewichtsfunktionen.
Wir wollen die wichtigsten Ergebnisse der Theorie kurz anführen.
Um orthogonale Polynome einzuführen sei das Intervall ![]() und die Gewichtsfunktion
und die Gewichtsfunktion ![]() festgelegt.
Man definiert die Zahl
festgelegt.
Man definiert die Zahl
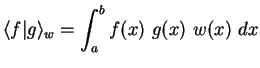 |
(4.46) |
| (4.47) |
Man kann eine Menge von Polynomen finden, so dass
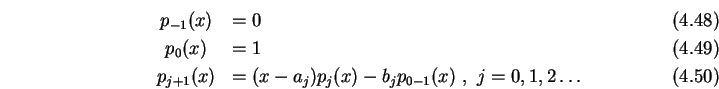
| (4.48) |
Der Term höchster Ordnung
![]() in
in ![]() hat den
Koeffizienten 1! Die
hat den
Koeffizienten 1! Die ![]() lassen sich normieren indem man durch
lassen sich normieren indem man durch
![]() dividiert. Man beachte aber, dass die
Koeffizienten
dividiert. Man beachte aber, dass die
Koeffizienten ![]() davon abhängen wie man normiert. Es
läßt sich zeigen, dass
davon abhängen wie man normiert. Es
läßt sich zeigen, dass ![]() genau
genau ![]() verschiedene
Nullstellen hat. Ausserdem liegt zwischen je zwei Nullstellen von
verschiedene
Nullstellen hat. Ausserdem liegt zwischen je zwei Nullstellen von
![]() genau eine Nullstelle von
genau eine Nullstelle von ![]()
Der Hauptsatz der Gauß-Quadratur ist nun:
Die gesuchten Stützstellen ![]() der
der ![]() -Punkt-Regel in Gleichung
(
-Punkt-Regel in Gleichung
(![]() ) sind gerade die Nullstellen des orthogonalen
Polynoms
) sind gerade die Nullstellen des orthogonalen
Polynoms ![]() zur Gewichtsfunktion
zur Gewichtsfunktion ![]() .
.
Die Gewichte ![]() werden dann so bestimmt, dass die Formel
(
werden dann so bestimmt, dass die Formel
(![]() ) für
) für
![]() mit
mit
![]() exakt ist. Das führt auf
exakt ist. Das führt auf ![]() Gleichungen.
Gleichungen.
(Die Nullen rechts sind Folge der Orthogonalität).
Man kann zeigen, dass mit den aus (![]() )
berechneten Gewichten Gleichung (
)
berechneten Gewichten Gleichung (![]() ) auch
für
) auch
für
![]() mit
mit
![]() exakt
ist. Da jedes Polynom der Ordnung
exakt
ist. Da jedes Polynom der Ordnung ![]() oder niedriger als
Linearkombination der
oder niedriger als
Linearkombination der ![]() geschrieben werden kann, ist
somit die Gaussche Quadratur Formel (
geschrieben werden kann, ist
somit die Gaussche Quadratur Formel (![]() )
auch für alle Polynome mit Ordnung kleiner als
)
auch für alle Polynome mit Ordnung kleiner als ![]() exakt.
exakt.
Die Gauß-Quadratur besteht also im allgemeinen aus drei Schritten:
Für ungewöhnliche Gewichtsfunktionen ![]() kann das Aufstellen einer
Gauß-Quadratur jedoch mühsam werden.
kann das Aufstellen einer
Gauß-Quadratur jedoch mühsam werden.
Die gebräuchlichsten Gauß-Quadraturen sind nach den orthogonalen Polynomen benannt.
Gauss-Legendre:
![\begin{eqnarray*}w(x)=1, \hspace*{1cm}-1<x<1\ [6pt]
(j+1)P_{j+1}=(2j+1)x P_j -j P_{j-1}
\end{eqnarray*}](img412.gif)
Gauss-Tschebyschew:
![\begin{eqnarray*}w(x)=\frac{1}{\sqrt{1-x^2}}, \hspace*{1cm} -1<x<1\ [6pt]
T_j+1+2xT_j-T_{j-1}
\end{eqnarray*}](img413.gif)
Gauss-Laguerre
![\begin{eqnarray*}w(x)=x^{\alpha}e^{-x}, \hspace*{1cm} 0<x<\infty\ [6pt]
(j+1)L^...
..._{j+1}=(-x+2j+\alpha+1)L^{\alpha}_j
-(j+\alpha)L^{\alpha}_{j-1}
\end{eqnarray*}](img414.gif)
Gauss-Hermite
![\begin{eqnarray*}w(x)=e^{-x^2},\hspace*{1cm} -\infty < x < \infty\ [6pt]
H_{j+1}=2xH_j-2jH_{j-1}
\end{eqnarray*}](img415.gif)
Manche dieser Polynome treten bei der Lösung spezieller
Probleme in der Quantenmechanik und Elekrodynamik auf.