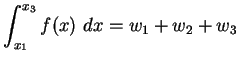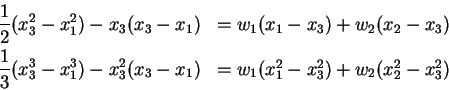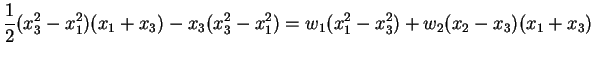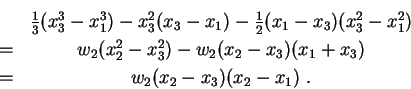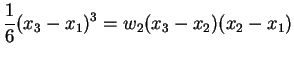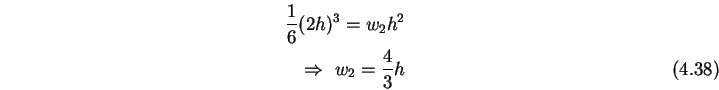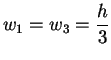Next: Beliebige Stützstellen
Up: Gauß - Quadratur
Previous: Lineare Näherung : L=2
Für 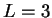 steht in (
steht in (![[*]](file:/mnt/bison/local/lib/latex2html/icons/crossref.gif) )
)
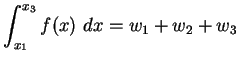 |
(4.33) |
Jetzt fordert man, dass (![[*]](file:/mnt/bison/local/lib/latex2html/icons/crossref.gif) )
für
)
für
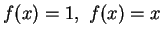 , und
, und 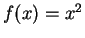 exakt ist.
exakt ist.
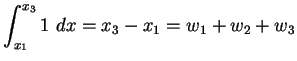 |
(4.34) |
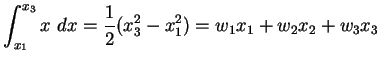 |
(4.35) |
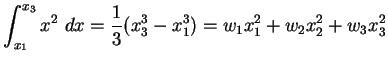 |
(4.36) |
Lösung des Gleichungssystems: Multipliziere (![[*]](file:/mnt/bison/local/lib/latex2html/icons/crossref.gif) ) mit
) mit
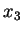 bzw.
bzw. 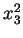 ,und subtrahiere dieses von (
,und subtrahiere dieses von (![[*]](file:/mnt/bison/local/lib/latex2html/icons/crossref.gif) )
und (
)
und (![[*]](file:/mnt/bison/local/lib/latex2html/icons/crossref.gif) ).
Das gibt:
).
Das gibt:
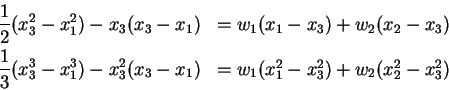
Nun multipliziere die erste Gleichung mit mit 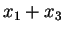
Subtraktion ergibt
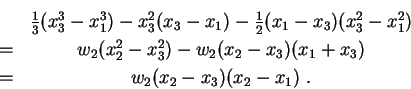
Ausrechnen liefert
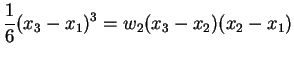 |
(4.37) |
oder
Weiter findet man
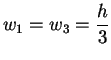 |
(4.38) |
also insgesamt die Simpsonregel. Mit zunehmendem 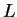 steigt die Zahl
der zu wählenden Gewichte
steigt die Zahl
der zu wählenden Gewichte 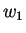 und die Genauigkeit.
und die Genauigkeit.




Next: Beliebige Stützstellen
Up: Gauß - Quadratur
Previous: Lineare Näherung : L=2
© R.Hilfer et al., ICA-1, Univ. Stuttgart
28.6.2002