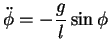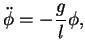Next: Allgemeine Form der Beispiele
Up: Anfangswertprobleme
Previous: Die Trommelfellgleichung
Eine punktförmige Masse 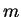 ist an einem starren masselosen Stab der
Länge
ist an einem starren masselosen Stab der
Länge 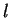 aufgehängt und schwingt reibungsfrei im Schwerefeld
aufgehängt und schwingt reibungsfrei im Schwerefeld
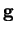 . Es sei
. Es sei 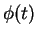 der Auslenkungswinkel aus der Ruhelage
der Auslenkungswinkel aus der Ruhelage
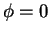 . Der Stab mit Anfangsauslenkung
. Der Stab mit Anfangsauslenkung
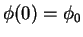 |
(5.16) |
und der Stab in der Ruhelage 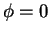 bilden eine Ebene. Das Pendel
schwingt in der Ebene. Das Pendel schwingt in dieser Ebene wenn es mit
Anfangswinkelgeschwindigkeit
bilden eine Ebene. Das Pendel
schwingt in der Ebene. Das Pendel schwingt in dieser Ebene wenn es mit
Anfangswinkelgeschwindigkeit
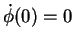 |
(5.17) |
losgelassen wird. In diesem Fall reicht der Energiesatz um die
Lösung zu finden. Die Gesamtenergie 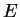 ist erhalten, das heißt
ist erhalten, das heißt
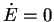 bzw.
bzw. 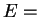 const. Der Energiesatz lautet dann für die
die zweidimensionale Bewegung:
const. Der Energiesatz lautet dann für die
die zweidimensionale Bewegung:
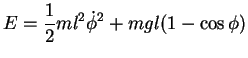 |
(5.18) |
Wir nehmen an 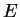 ist so klein, dass es stets einen Umkehrpunkt
ist so klein, dass es stets einen Umkehrpunkt
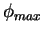 (=maximale Auslenkung) gibt. Für
(=maximale Auslenkung) gibt. Für
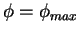 gilt
gilt
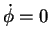 |
(5.19) |
also
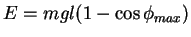 |
(5.20) |
also eingesetzt in (![[*]](file:/mnt/bison/local/lib/latex2html/icons/crossref.gif) ) folgt
) folgt
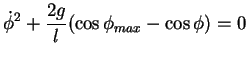 |
(5.21) |
und damit
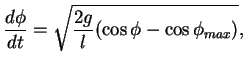 |
(5.22) |
oder nach Trennung der Variablen
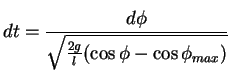 |
(5.23) |
Nun setzen wir
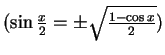
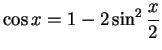 |
(5.24) |
ein und finden
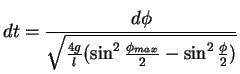 |
(5.25) |
oder
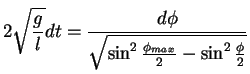 |
(5.26) |
Nun setzen wir
und somit:
so dass folgt
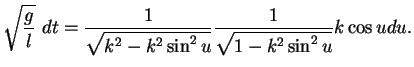 |
(5.27) |
Schließlich folgt
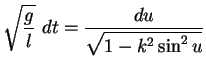 |
(5.28) |
und somit durch Integration von 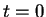 bis
bis 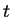 und
und
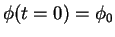 bis
bis 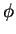
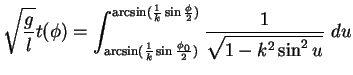 |
(5.29) |
Dies ist ein elliptisches Integral, das sich nicht mehr weiter
vereinfachen läßt. Man könnte es aber numerisch mit
Gaussscher Quadratur auswerten und hätte mit 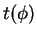 dann
auch die Umkehrfunktion
dann
auch die Umkehrfunktion 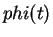 gefunden.
gefunden.
Statt das Integral direkt auszuwerten, könnte man auch eine
nichtlineare Differentialgleichung direkt diskretisieren und lösen,
um die numerische Lösung zu erhalten. Dazu wird der Energiesatz
(![[*]](file:/mnt/bison/local/lib/latex2html/icons/crossref.gif) ) einmal differenziert so dass dann folgt
) einmal differenziert so dass dann folgt
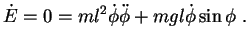 |
(5.30) |
Daraus folgt die Differntialgleichung
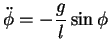 |
(5.31) |
für das ebene mathematische Pendel. Diese Gleichung ist wieder
nichtlinear. Für kleine Auslenkungen
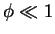 ist
ist
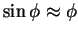 und man erhält als lineare Näherung
und man erhält als lineare Näherung
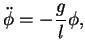 |
(5.32) |
d.h. wieder den harmonischen Oszillator.




Next: Allgemeine Form der Beispiele
Up: Anfangswertprobleme
Previous: Die Trommelfellgleichung
© R.Hilfer et al., ICA-1, Univ. Stuttgart
28.6.2002
![]() ist an einem starren masselosen Stab der
Länge
ist an einem starren masselosen Stab der
Länge ![]() aufgehängt und schwingt reibungsfrei im Schwerefeld
aufgehängt und schwingt reibungsfrei im Schwerefeld
![]() . Es sei
. Es sei ![]() der Auslenkungswinkel aus der Ruhelage
der Auslenkungswinkel aus der Ruhelage
![]() . Der Stab mit Anfangsauslenkung
. Der Stab mit Anfangsauslenkung
![]() ist so klein, dass es stets einen Umkehrpunkt
ist so klein, dass es stets einen Umkehrpunkt
![]() (=maximale Auslenkung) gibt. Für
(=maximale Auslenkung) gibt. Für
![]() gilt
gilt
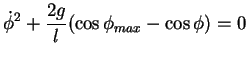
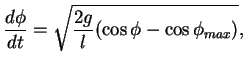
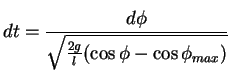
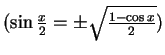
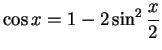
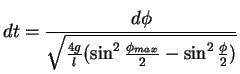
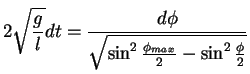
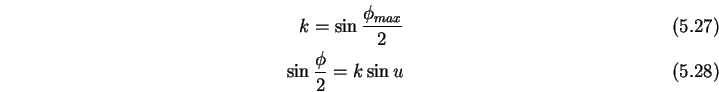
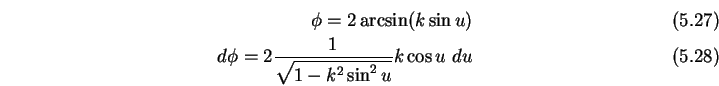
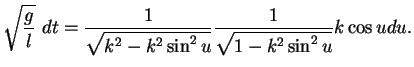
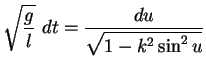
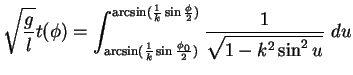
![]() ) einmal differenziert so dass dann folgt
) einmal differenziert so dass dann folgt