1 Introduction
[page 637, §1]
[637.1.1] A special function of growing importance
is the generalized Mittag-Leffler function defined
by the power series [2, p. 210]
| (1) |
for complex argument ![]() and parameters
and parameters ![]() with
with ![]() .
[637.1.2] Despite the fact that
.
[637.1.2] Despite the fact that ![]() was introduced roughly 100 years ago
[3, 4, 5, 6, 7, 8]
its mapping properties in the complex plane are largely unknown.
was introduced roughly 100 years ago
[3, 4, 5, 6, 7, 8]
its mapping properties in the complex plane are largely unknown.
[637.2.1] Mittag-Leffler functions are important in mathematical as well as in theoretical and applied physics [9, 10, 11, 12, 13, 14, 15, 16, 17, 18]. [637.2.2] A primary reason for the recent surge of interest in these functions [page 638, §0] is their appearance when solving the fractional differential equation
| (2) |
where ![]() is a fractional derivative of
order
is a fractional derivative of
order ![]() and type
and type ![]() with lower limit
with lower limit ![]() [18].
[638.0.1] In eq. (2) the symbol
[18].
[638.0.1] In eq. (2) the symbol
![]() stands for [18, p. 115]
stands for [18, p. 115]
| (3) |
for functions for which the expression on the right hand side exists.
[638.0.2] Of course, the notation
![]() stands for the right sided
fractional Riemann-Liouville integral of order
stands for the right sided
fractional Riemann-Liouville integral of order
![]() defined by
defined by
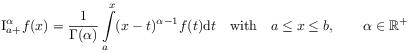 |
(4) |
for locally integrable functions ![]() .
[638.0.3] Recall from Ref. [18, p. 115]
that equation (2)
is solved for
.
[638.0.3] Recall from Ref. [18, p. 115]
that equation (2)
is solved for ![]() by
by
| (5) |
where ![]() is the generalized Mittag-Leffler function.
[638.0.4] Equation (2) shows that the Mittag-Leffler function
plays the same role for fractional calculus that the exponential
function plays for conventional calculus.
[638.0.5] Mittag-Leffler functions and fractional calculus have
in recent years become a powerful tool to
investigate anomalous dynamics and strange kinetics
[13, 18, 19, 20].
is the generalized Mittag-Leffler function.
[638.0.4] Equation (2) shows that the Mittag-Leffler function
plays the same role for fractional calculus that the exponential
function plays for conventional calculus.
[638.0.5] Mittag-Leffler functions and fractional calculus have
in recent years become a powerful tool to
investigate anomalous dynamics and strange kinetics
[13, 18, 19, 20].
[638.1.1] Despite the growing importance of ![]() in physics, and despite a wealth of analytical information
about
in physics, and despite a wealth of analytical information
about ![]() its behaviour as a holomorphic
function and dependence upon the parameters are largely
unexplored, because
there seem to be no numerical algorithms available
to compute the function accurately for all
its behaviour as a holomorphic
function and dependence upon the parameters are largely
unexplored, because
there seem to be no numerical algorithms available
to compute the function accurately for all ![]() ,
, ![]() ,
, ![]() .
[638.1.2] Easy numerical evaluation and a thorough understanding of
.
[638.1.2] Easy numerical evaluation and a thorough understanding of
![]() as a function of
as a function of ![]() ,
, ![]() ,
, ![]() is, however,
a key prerequisite for extending its applications to other disciplines.
[638.1.3] It is therefore desirable to explore the behaviour of
is, however,
a key prerequisite for extending its applications to other disciplines.
[638.1.3] It is therefore desirable to explore the behaviour of
![]() for large sets of the parameters
for large sets of the parameters ![]() ,
, ![]() and complex argument
and complex argument ![]() .
.
[638.2.1] Given this objective the present paper reports
a newly developed numerical algorithm as well as
extensive computations for the generalized Mittag-Leffler function.
[638.2.2] Little will be said in this paper about the algorithm apart from
giving its complete definition
a (This is a footnote:) aWhile this work was in progress a simpler algorithm
appeared in [24].
A detailed comparison between the two algorithms
can be found in [25]..
[638.2.3] One should note that the algorithm works not only on the real axis,
but in the full complex plane.
[638.2.4] Rather than discussing details of the algorithm we concentrate here
on exploring the functional behaviour of ![]() .
[638.2.5] In particular we study its complex zeros and illustrate
its behaviour as an entire function.
[638.2.6] As an example we find that the zeros of
.
[638.2.5] In particular we study its complex zeros and illustrate
its behaviour as an entire function.
[638.2.6] As an example we find that the zeros of ![]() coalesce to form a simple pole in the limit
coalesce to form a simple pole in the limit ![]() .
[638.2.7] Moreover, the zeros diverge in a complicated
fashion to
.
[638.2.7] Moreover, the zeros diverge in a complicated
fashion to ![]() as
as ![]() approaches unity
from above as well as from below.
approaches unity
from above as well as from below.
