2 Method of Calculation

[page 639, §1]

2.1 Recursion Relation

[639.1.1] In the rest of this paper $\alpha$ and $\beta$ are real numbers with $\alpha>0$ . [639.1.2] Calculating $\mbox{\rm E}_{{\alpha,\beta}}(z)$ for the case $\alpha>1$ can be reduced to the case $0<\alpha\leq 1$ by virtue of the recursion relation [2, 21]

$\mbox{\rm E}_{{\alpha,\beta}}(z)=\frac{1}{2m+1}\sum _{{h=-m}}^{m}\mbox{\rm E}_{{{\alpha/(2m+1)},\beta}}(z^{{1/(2m+1)}}e^{{2\pi{\rm i}h/(2m+1)}})$

(6)

valid for all $\beta\in\mathbb{R}$ , $z\in\mathbb{C}$ where $m=[(\alpha-1)/2]+1$ . [639.1.3] Here $[x]$ denotes the largest integer smaller than $x$ . [639.1.4] Because of the recursion we consider only the case $0<\alpha\leq 1$ in the following.

2.2 Regions

[639.2.1] For $0<\alpha\leq 1$ the complex $z$ -plane is partitioned into four regions $\mathbb{G}_{0}$ , $\mathbb{G}_{1}$ , $\mathbb{G}_{2}$ , $\mathbb{G}_{3}$ . [639.2.2] In each region a different method is used for the calculation of the Mittag-Leffler function. [639.2.3] The central region

$\mathbb{G}_{0}=\overline{\mathbb{D}(r_{0})}=\{ z\in\mathbb{C}:|z|\leq r_{0}\}$

(7)

is the closure of the open disk $\mathbb{D}(r_{0})=\{ z\in\mathbb{C}:|z|<r_{0}\}$ of radius $r_{0}<1$ centered at the origin. [639.2.4] In our numerical calculations we have chosen $r_{0}=0.9$ throughout. [639.2.5] The regions $\mathbb{G}_{1},\mathbb{G}_{2}$ are defined by

$\displaystyle\mathbb{G}_{1}$	$\displaystyle=\mathbb{W}^{+}(5\pi\alpha/6)\setminus\mathbb{G}_{0}$		(8)
$\displaystyle\mathbb{G}_{2}$	$\displaystyle=\mathbb{C}\setminus(\mathbb{G}_{1}\cup\mathbb{G}_{0})$		(9)

where

$\mathbb{W}^{+}(\phi)=\{ z\in\mathbb{C}:|\arg(z)|<\phi\}$

(10)

is the open wedge with opening angle $\phi,\,(0<\phi<\pi)$ . [639.2.6] For future reference we define also the (left) wedge

$\mathbb{W}^{-}(\phi)=\{ z\in\mathbb{C}:\phi<|\arg(z)|\leq\pi\}$

(11)

[639.2.7] Finally the region $\mathbb{G}_{3}$ is defined as

$\mathbb{G}_{3}=\mathbb{C}\setminus\mathbb{D}(r_{1})=\{ z\in\mathbb{C}:|z|>r_{1}\}$

(12)

where $r_{1}>r_{0}$ will be defined below.

2.3 Taylor series

[639.3.1] For $z\in\mathbb{G}_{0}$ , i.e. for the central disk region (with $r_{0}=0.9$ ), the Mittag-Leffler function is computed from truncating its Taylor series (1). [639.3.2] For given $z\in\mathbb{G}_{0}$ and accuracy $\epsilon$ we choose [page 640, §0] $N$ such that

$\left|\mbox{\rm E}_{{\alpha,\beta}}(z)-\sum _{{k=0}}^{N}\frac{z^{k}}{\Gamma(\alpha k+\beta)}\right|\leq\epsilon$

(13)

holds. [640.0.1] The dependence of $N$ on the accuracy $\epsilon$ and other parameters is found as

$N\geq\max\Big\{\left[(2-\beta)/\alpha\right]+1,\left[\frac{\ln(\epsilon(1-|z|))}{\ln(|z|)}\right]+1\Big\}.$

(14)

2.4 Integral Representations

[640.1.1] We start from the basic integral representation [2, p. 210]

$\mbox{\rm E}_{{\alpha,\beta}}(z)=\frac{1}{2\pi{\rm i}}\int\limits _{{\mathcal{C}}}\frac{y^{{\alpha-\beta}}{\mathrm{e}}^{y}}{y^{\alpha}-z}\mbox{\rm d}y$

(15)

where the path of integration $\mathcal{C}$ in the complex plane starts and ends at $-\infty$ and encircles the circular disc $|y|\leq|z|^{{1/\alpha}}$ in the positive sense. [640.1.2] When this integral is evaluated several cases arise. [640.1.3] For $z\in\mathbb{G}_{1}$ we distinguish the cases $\beta\leq 1$ and $\beta>1$ and compute the Mittag-Leffler function from the integral representations [22]

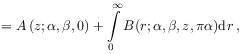$\displaystyle\mbox{\rm E}_{{\alpha,\beta}}(z)$	$\displaystyle=A\left(z;\alpha,\beta,0\right)+\int\limits _{0}^{\infty}B(r;\alpha,\beta,z,\pi\alpha)\mbox{\rm d}r\,,$		$\displaystyle\beta\leq 1$		(16)
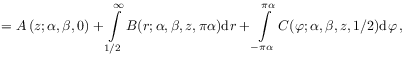$\displaystyle\mbox{\rm E}_{{\alpha,\beta}}(z)$	$\displaystyle=A\left(z;\alpha,\beta,0\right)+\int\limits _{{1/2}}^{\infty}B(r;\alpha,\beta,z,\pi\alpha)\mbox{\rm d}r+\int\limits _{{-\pi\alpha}}^{{\pi\alpha}}C(\varphi;\alpha,\beta,z,1/2)\mbox{\rm d}\varphi\,,$		$\displaystyle\beta>1$		(17)

where

$A(z;\alpha,\beta,x)=\frac{1}{\alpha}z^{{(1-\beta)/\alpha}}\exp\left[z^{{1/\alpha}}\cos(x/\alpha)\right]$

(18)

$B(r;\alpha,\beta,z,\phi)=\frac{1}{\pi}A(r;\alpha,\beta,\phi)\frac{r\sin[\omega(r,\phi,\alpha,\beta)-\phi]-z\sin[\omega(r,\phi,\alpha,\beta)]}{r^{2}-2rz\cos\phi+z^{2}}$

(19)

$C(\varphi;\alpha,\beta,z,\rho)=\frac{\rho}{2\pi}A(\rho;\alpha,\beta,\varphi)\frac{\cos[\omega(\rho,\varphi,\alpha,\beta)]+{\rm i}\sin[\omega(\rho,\varphi,\alpha,\beta)]}{\rho(\cos\varphi+{\rm i}\sin\varphi)-z}$

(20)

$\omega(x,y,\alpha,\beta)=x^{{1/\alpha}}\sin(y/\alpha)+y(1+(1-\beta)/\alpha).$

(21)

[640.1.4] For $z\in\mathbb{G}_{2}$ the integral representations read

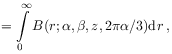$\displaystyle\mbox{\rm E}_{{\alpha,\beta}}(z)$	$\displaystyle=\int\limits _{0}^{\infty}B(r;\alpha,\beta,z,2\pi\alpha/3)\mbox{\rm d}r\,,$		$\displaystyle\beta\leq 1$		(22)
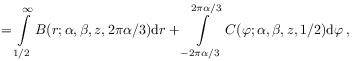$\displaystyle\mbox{\rm E}_{{\alpha,\beta}}(z)$	$\displaystyle=\int\limits _{{1/2}}^{\infty}B(r;\alpha,\beta,z,2\pi\alpha/3)\mbox{\rm d}r+\int\limits _{{-2\pi\alpha/3}}^{{2\pi\alpha/3}}C(\varphi;\alpha,\beta,z,1/2)\mbox{\rm d}\varphi\,,$		$\displaystyle\beta>1$		(23)

where the integrands have been defined in eq. (18)–(21) above.

[page 641, §1]
[641.1.1] The integrand $C(\varphi;\alpha,\beta,z,\rho)$ is oscillatory but bounded over the integration interval. [641.1.2] Thus the integrals over $C$ can be evaluated numerically using any appropriate quadrature formula. [641.1.3] We use a robust Gauss-Lobatto quadrature.

[641.2.1] The integrals over $B(r;\alpha,\beta,z,\phi)$ involve infinite intervals. [641.2.2] For given $z\in\mathbb{G}_{1}$ (resp. $z\in\mathbb{G}_{2}$ ) and accuracy $\epsilon$ we approximate the integrals by truncation. [641.2.3] The error

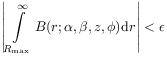$\left|\int\limits _{{{R_{{\rm max}}}}}^{\infty}B(r;\alpha,\beta,z,\phi)\mbox{\rm d}r\right|<\epsilon$

(24)

depends on the truncation point ${R_{{\rm max}}}$ . [641.2.4] For $\phi=\pi\alpha$ we find

${R_{{\rm max}}}\geq\left\{\begin{array}[]{ll}\max\left\{ 1,\, 2|z|,\,\left(-\ln\frac{\displaystyle\pi\epsilon}{\displaystyle 6}\right)^{\alpha}\right\},&\beta\geq 0\\ \\ \max\left\{(|\beta|+1)^{\alpha},\, 2|z|,\,\left(-2\ln\left(\frac{\displaystyle\pi\epsilon}{\displaystyle 6(|\beta|+2)(2|\beta|)^{{|\beta|}}}\right)\right)^{\alpha}\right\},&\beta<0,\\ \end{array}\right.$

(25)

while for $\phi=2\pi\alpha/3$ we have

${R_{{\rm max}}}\geq\left\{\begin{array}[]{ll}\max\left\{ 2^{\alpha},\, 2|z|,\,\left(-2\ln\frac{\displaystyle\pi 2^{\beta}\epsilon}{\displaystyle 12}\right)^{\alpha}\right\},&\beta\geq 0\\ \\ \max\left\{[2(|\beta|+1)]^{\alpha},\, 2|z|,\left[-4\ln\frac{\displaystyle\pi 2^{\beta}\epsilon}{\displaystyle 12\left(|\beta|+2\right)(4|\beta|)^{{|\beta|}}}\right]^{\alpha}\right\},&\beta<0.\end{array}\right.$

(26)

2.5 Exponential Asymptotics

[641.3.1] The asymptotic expansions given in eqs. (21) and (22) on page 210 in Ref. [2] indicate that the Mittag-Leffler function exhibits a Stokes phenomenon. [641.3.2] The Stokes lines are the rays $\arg(z)=\pm\alpha\pi$ and it was recently shown in [23] that a Berry-type smoothing applies. [641.3.3] The exponentially improved asymptotic expansions will be used here for computing $\mbox{\rm E}_{{\alpha,\beta}}(z)$ for $z\in\mathbb{G}_{3}$ . [641.3.4] More precisely for $0<\alpha<1$ we use the following exponentially improved uniform asymptotic expansions [23] :

$\mbox{\rm E}_{{\alpha,\beta}}(z)=-\sum _{{k=1}}^{M}\frac{z^{{-k}}}{\Gamma(\beta-\alpha k)}+O\left(|z|^{{(1/2-\beta)/\alpha}}{\mathrm{e}}^{{-|z|^{{1/\alpha}}}}\right)$

(27)

for $z\in\mathbb{G}_{3}\cap\mathbb{W}^{-}(\alpha\pi+\delta)$

$\mbox{\rm E}_{{\alpha,\beta}}(z)=\frac{1}{\alpha}z^{{(1-\beta)/\alpha}}{\mathrm{e}}^{{z^{{1/\alpha}}}}-\sum _{{k=1}}^{M}\frac{z^{{-k}}}{\Gamma(\beta-\alpha k)}+O\left(|z|^{{(1/2-\beta)/\alpha}}{\mathrm{e}}^{{-|z|^{{1/\alpha}}}}\right)$

(28)

for $z\in\mathbb{G}_{3}\cap\mathbb{W}^{+}(\alpha\pi-\delta)$ ,

$\displaystyle\mbox{\rm E}_{{\alpha,\beta}}(z)$	$\displaystyle=\frac{1}{2\alpha}z^{{(1-\beta)/\alpha}}{\mathrm{e}}^{{z^{{1/\alpha}}}}\operatorname{erfc}\left((c^{3}/36-{\rm i}c^{2}/6-c)\sqrt{\|z\|^{{1/\alpha}}/2}\right)$
	$\displaystyle-\sum _{{k=1}}^{M}\frac{z^{{-k}}}{\Gamma(\beta-\alpha k)}+O\left(\|z\|^{{(1/2-\beta)/\alpha}}{\mathrm{e}}^{{-\|z\|^{{1/\alpha}}}}\right)$		(29)

[page 642, §0] for $z\in\mathbb{G}_{3}$ with $-\alpha\pi-\delta\leq\arg(z)\leq-\alpha\pi+\delta$ and $c=\arg(z^{{1/\alpha}})+\pi$ , and

$\displaystyle\mbox{\rm E}_{{\alpha,\beta}}(z)$	$\displaystyle=\frac{1}{2\alpha}z^{{(1-\beta)/\alpha}}{\mathrm{e}}^{{z^{{1/\alpha}}}}\operatorname{erfc}\left((c+{\rm i}c^{2}/6-c^{3}/36)\sqrt{\|z\|^{{1/\alpha}}/2}\right)$
	$\displaystyle-\sum _{{k=1}}^{M}\frac{z^{{-k}}}{\Gamma(\beta-\alpha k)}+O\left(\|z\|^{{(1/2-\beta)/\alpha}}{\mathrm{e}}^{{-\|z\|^{{1/\alpha}}}}\right)$		(30)

for $z\in\mathbb{G}_{3}$ with $\alpha\pi-\delta\leq\arg(z)\leq\alpha\pi+\delta$ and $c=\arg(z^{{1/\alpha}})-\pi$ . [642.0.1] Here $\delta>0$ is a small number, in practice we use $\delta=0.01$ . [642.0.2] In eqs. (2.5) and (2.5)

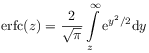$\operatorname{erfc}(z)=\frac{2}{\sqrt{\pi}}\int\limits _{z}^{\infty}{\mathrm{e}}^{{y^{2}/2}}\mbox{\rm d}y$

(31)

denotes the complex complementary error function. [642.0.3] Note the difference between eqs. (27)–(2.5) and the expansions in [2, p. 210]. [642.0.4] We take

$M=\min\{ 50,[|z|^{{1/\alpha}}/\alpha]\}$

(32)

to truncate the asymptotic series. [642.0.5] Choosing for $\epsilon$ the machine precision we fix the radius $r_{1}$ in $\mathbb{G}_{3}$ at

$r_{1}=\frac{1}{[\epsilon\Gamma(\beta-\alpha M)]^{{1/M}}}.$

(33)

[642.0.6] The remainder estimates in eqs. (27)–(2.5) are only valid for a value of $M$ that is chosen in an optimal sense as in eqs. (32) and (33).

Authors:	R. Hilfer und H.J. Seybold
originally published in:	Integral Transforms and Special Functions Vol. 17, 637-652 (2006)
originally submitted:	March 21st, 2005