4 Inverse Mittag-Leffler functions

[647.7.1] We introduce the inverse generalized Mittag-Leffler functions $\mbox{\rm L}_{{\alpha,\beta}}(z)$ as the solutions of the equation

$\mbox{\rm L}_{{\alpha,\beta}}(\mbox{\rm E}_{{\alpha,\beta}}(z))=z.$

(43)

[647.7.2] Our ability to calculate $\mbox{\rm E}_{{\alpha,\beta}}(z)$ allows us to evaluate also $\mbox{\rm L}_{{\alpha,\beta}}(z)$ by solving this functional equation numerically. [647.7.3] We have succeeded to determine the principal branch of $\mbox{\rm L}_{{\alpha,\beta}}(z)$ in such a way that three conditions are fulfilled. [647.7.4] 1. The function $\mbox{\rm L}_{{\alpha,\beta}}(z)$ is single valued and well defined on its principal branch. [647.7.5] 2. Its principal branch reduces to the principal branch of the logarithm for $\alpha\to 1$ . [647.7.6] 3. Its principal branch is a simply connected subset of the complex plane. [647.7.7] Figure 15 shows the principal branch for the case $\alpha=0.95$ , $\beta=1$ .

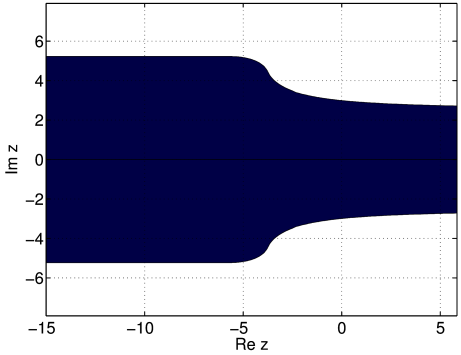
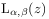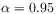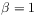Figure 15: The dark region corresponds to the principal branch of the inverse generalized Mittag-Leffler function $\mbox{\rm L}_{{\alpha,\beta}}(z)$ for $\alpha=0.95$ , $\beta=1$ .

Authors:	R. Hilfer und H.J. Seybold
originally published in:	Integral Transforms and Special Functions Vol. 17, 637-652 (2006)
originally submitted:	March 21st, 2005