Sie sind hier: ICP » R. Hilfer » Publikationen

1 Introduction

[page 89, §1]   
[89.1.1] A large number of problems in theoretical physics, including Schrödingers, Maxwell and Newtons equations, can be formulated as initial value problems for dynamical evolution equations of the form

\frac{\mbox{\rm d}}{\mbox{\rm d}t}f(t)=\mbox{\rm B}f(t) (1)

where t\in\mathbb{R} denotes time and B is an operator on a Banach space. [89.1.2] Depending on the initial data f(0)=f_{0} describing the state or observable of the system at time t=0 the problem is to find the state or observable f(t) of the system at later times t>0. a (This is a footnote:) a In classical mechanics the states are points in phase space, the observables are functions on phase space, and the operator B is specified by a vector field and Poisson brackets. In quantum mechanics (with finitely many degrees of freedom) the states correspond to rays in a Hilbert space, the observables to operators on this space, and the operator B to the Hamiltonian. In field theories the states are normalized positive functionals on an algebra of operators or observables, and then B becomes a derivation on the algebra of observables. The equations (1) need not be first order in time. An example is the initial-value problem for the wave equation for g(t,x)

\frac{\partial^{2}g}{\partial t^{2}}=c^{2}\frac{\partial^{2}g}{\partial x^{2}}
in one dimension. It can be recast into the form of eq. (1) by introducing a second variable h and defining
f=\begin{pmatrix}g\\ h\end{pmatrix}\text{\ \ \ \ }\mbox{\rm and}\text{\ \ \ \ }\mbox{\rm B}=\begin{pmatrix}0&1\\ 1&0\end{pmatrix}c\frac{\partial}{\partial x}

[89.2.1] Many authors, mostly driven by the needs of applied problems, have considered generalizations of equation (1) of the form

\frac{{\rm"}\mbox{\rm d}^{\alpha}{\rm"}}{\mbox{\rm d}t^{\alpha}}f(t)=\mbox{\rm B}f(t) (2)

in which the first order time derivative \mbox{\rm d}/\mbox{\rm d}t is replaced with a certain fractional time derivative ‘‘\mbox{\rm d}^{\alpha}/\mbox{\rm d}t^{\alpha}’’ of order \alpha>0 (see e.g.  [1]–[24] and the Chapters IV–VIII  in this book). [89.2.2] A number of fundamental questions are raised by such a replacement. [89.2.3] In order to appreciate these it is useful to recall that the appearance of \mbox{\rm d}/\mbox{\rm d}t in eq. (1) reflects not only a basic symmetry of nature but also the basic principle of locality. [89.2.4] Of course, the symmetry in question is time translation invariance. [89.2.5] Remember that

\frac{\mbox{\rm d}}{\mbox{\rm d}s}f(s)=\lim _{{t\to 0}}\frac{f(s)-f(s-t)}{t}=-\lim _{{t\to 0}}\frac{{\mathcal{T}}(t)f(s)-f(s)}{t} (3)

[page 90, §0]    identifies -\mbox{\rm d}/\mbox{\rm d}t as the infinitesimal generator of time translations b (This is a footnote:) b A simple translation with unit "speed" reflects the idea of time "flowing" uniformly with constant velocity. This idea is embodied in measuring time by comparison with periodic processes (clocks). A competing idea, related to the flow of time represented by eq. (5), is to measure time by comparison with nonperiodic clocks such as decay or aging processes. defined by

{\mathcal{T}}(t)f(s)=f(s-t). (4)

[90.0.1] Equation (2) abandons {\mathcal{T}}(t) as the general time evolution, and this raises the question what replaces eq. (4), and how a fractional derivative can arise as the generator of a physical time evolution. [90.0.2] Most workers in fractional calculus have avoided these questions, and my purpose in this chapter is to review and discuss an answer provided recently in [6, 7, 8, 9, 10, 11].

[90.1.1] Derivatives of fractional order 0<\alpha\leq 1 were found to emerge quite generally as the infinitesimal generators of coarse grained macroscopic time evolutions given by [6, 7, 8, 9, 10, 11]

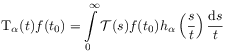\mbox{\rm T}_{\alpha}(t)f(t_{0})=\int\limits _{0}^{\infty}{\mathcal{T}}(s)f(t_{0})h_{\alpha}\left(\frac{s}{t}\right)\frac{\mbox{\rm d}s}{t} (5)

where t\geq 0 and 0<\alpha\leq 1. [90.1.2] Explicit expressions for the kernels h_{\alpha}(x) for all 0<\alpha\leq 1 are given in eq. (69) below. [90.1.3] It is the main objective of this chapter to show that (in a certain sense) all macroscopic time evolutions have the form of eq. (5), and that fractional time derivatives are their infinitesimal generators.

[90.2.1] Given the great difference between \mbox{\rm T}_{\alpha}(t) in eq. (5) and \mbox{\rm T}_{1}(t)={\mathcal{T}}(t) in eq. (4) it becomes clear that basic issues, such as irreversibility, translation symmetry, or the meaning of stationarity are inevitably involved when proposing fractional dynamics. [90.2.2] Let me therefore advance the basic postulate that all time evolutions of physical systems are irreversible. [90.2.3] Obviously this law of irreversibility must be considered to be an empirical law of nature equal in rank to the law of energy conservation. [90.2.4] Reversible behaviour is an idealization. [90.2.5] Its validity or applicability in physical experiments depends on the degree to which the system can be isolated (or decoupled) from its past history and its environment. [90.2.6] According to this view the irreversible flow of time is more fundamental than the time reversal symmetry of Newtons or other equations. [90.2.7] My starting point is therefore that for a general time evolution operator \mbox{\rm T}(t) the evolution parameter t is not a time instant (which could be positive or negative), but a duration, which cannot be negative.

[90.3.1] An immediate consequence of the postulated law of irreversibility is that the classical irreversibility problem of theoretical physics becomes reversed.

[page 91, §0]    [91.0.1] Now the theoretical task is not to explain how irreversibility arises from reversible evolution equations, but how seemingly reversible equations arise as idealizations from an underlying irreversible time evolution. [91.0.2] A possible explanation is provided by the present theory based on eq. (5). [91.0.3] It turns out that the case \alpha=1 in eq. (5) is of predominant mathematical and physical importance, because it is in a quantifiable sense a strong universal attractor. [91.0.4] In this case the kernel h_{1}(x) becomes

h_{1}(x)=\lim _{{\alpha\rightarrow 1^{-}}}h_{\alpha}(x)=\delta(x-1), (6)

and the time evolution \mbox{\rm T}_{1}(t)={\mathcal{T}}(t) in (5) reduces to a simple translation as in eq.(4). [91.0.5] T_{1}(t) with t\geq 0 is a representation of the time semigroup (\mathbb{R}_{+},+). [91.0.6] It can be extended to one of the full group (\mathbb{R},+). [91.0.7] This is not possible for T_{\alpha} with 0<\alpha<1. [91.0.8] The physical interpretation of \alpha is seen from \mathrm{supp}\, h_{\alpha}=\mathbb{R}_{+} for \alpha\neq 1 and \mathrm{supp}\, h_{1}=\{ 1\} for \alpha=1. [91.0.9] Hence the parameter \alpha classifies and quantifies the influence of the past history. [91.0.10] Small values of \alpha correspond to a strong influence of the past history. [91.0.11] For \alpha=1 the influence of the past history is minimal in the sense that it enters only through the present state.

[91.1.1] The basic result in eq. (5) was given in [6] and subsequently rationalized within ergodic theory by investigating the recurrence properties of induced automorphisms on subsets of measure zero [9, 10, 11]. [91.1.2] In these investigations the existence of a recurrent subset of measure zero had to be assumed. [91.1.3] Such an assumption becomes plausible from observations in low dimensional chaotic systems (see e.g. [25, 26] and Chapter V). [91.1.4] A rigorous proof for any given dynamical system, however, appears difficult, and it is therefore of interest to rederive the emergence of \mbox{\rm T}_{\alpha}(t) from a different, and more general, approach.