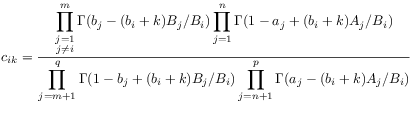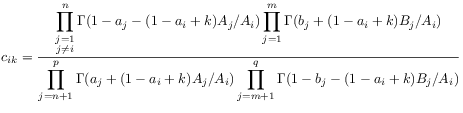4 H-Functions
4.1 Definition
[120.1.1] The ![]() -function of order
-function of order ![]() and with parameters
and with parameters
![]() ,
, ![]() ,
,
![]() , and
, and ![]() is defined for
is defined for ![]() by the contour integral
[55, 56, 57, 58, 59]
by the contour integral
[55, 56, 57, 58, 59]
| (153) |
where the integrand is
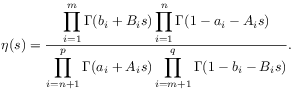 |
(154) |
[page 121, §0]
[121.0.1] In (153) ![]() and
and ![]() is not necessarily the principal value.
[121.0.2] The integers
is not necessarily the principal value.
[121.0.2] The integers ![]() must satisfy
must satisfy
| (155) |
and empty products are interpreted as being unity. [121.0.3] The parameters are restricted by the condition
| (156) |
where
| (157) |
are the poles of the numerator in (154). [121.0.4] The integral converges if one of the following conditions holds [59]
| (158a) | |||
| (158b) |
| (159a) | |||
| (159b) | |||
| (159c) |
| (160a) | |||
| (160b) | |||
| (160c) |
where ![]() .
[121.0.5] Here
.
[121.0.5] Here ![]() denotes a contour in the
complex plane starting at
denotes a contour in the
complex plane starting at ![]() and ending at
and ending at ![]() and
separating the points in
and
separating the points in ![]() from those
from those
[page 122, §0]
in ![]() , and the notation
, and the notation
| (161) | |||
| (162) | |||
| (163) | |||
| (164) |
was employed.
[122.0.1] The ![]() -functions are analytic for
-functions are analytic for ![]() and multivalued
(single valued on the Riemann surface of
and multivalued
(single valued on the Riemann surface of ![]() ).
).
4.2 Basic Properties
[122.1.1] From the definition of the ![]() -functions follow some basic properties.
[122.1.2] Let
-functions follow some basic properties.
[122.1.2] Let ![]() denote the symmetric group of
denote the symmetric group of ![]() elements,
and let
elements,
and let ![]() denote a permutation in
denote a permutation in ![]() .
[122.1.3] Then the product structure of (154) implies that
for all
.
[122.1.3] Then the product structure of (154) implies that
for all ![]() and
and ![]()
| (165) |
where the parameter permutations
| (166) | |||
have to be inserted on the right hand side.
[122.1.4] If any of ![]() or
or ![]() vanishes the corresponding permutation
is absent.
vanishes the corresponding permutation
is absent.
[122.2.1] The order reduction formula
| (167) |
[page 123, §0]
holds for ![]() and
and ![]() , and similarly
, and similarly
| (168) |
for ![]() and
and ![]() .
[123.0.1] The formula
.
[123.0.1] The formula
| (169) |
holds for ![]() and
and ![]() .
[123.0.2] Analogous formulae are readily found if a parameter pair
.
[123.0.2] Analogous formulae are readily found if a parameter pair ![]() or
or
![]() appears in one of the other groups.
appears in one of the other groups.
[123.1.1] A change of variables in (153) shows
| (170) |
which allows to transform an ![]() -function with
-function with ![]() and
and ![]() to one
with
to one
with ![]() and
and ![]() .
[123.1.2] For
.
[123.1.2] For ![]()
| (171) |
while for ![]()
| (172) |
[page 124, §0] holds.
[124.1.1] For ![]() with conditions (159) the integrand is analytic
and thus
with conditions (159) the integrand is analytic
and thus
| (173) |
4.3 Integral Transformations
[124.2.1] The definition of an ![]() -function in eq. (153)
becomes an inverse Mellin transform
if
-function in eq. (153)
becomes an inverse Mellin transform
if ![]() is chosen parallel to the imaginary axis
inside the strip
is chosen parallel to the imaginary axis
inside the strip
| (174) |
by the Mellin inversion theorem [60]. [124.2.2] Therefore
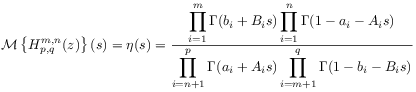 |
(175) |
whenever the inequality
| (176) |
is fulfilled.