2 Foundations
2.1 Basic Desiderata for Time Evolutions
[91.2.1] The following basic requirements define a time evolution in this chapter.
-
Semigroup
[91.2.2] A time evolution is a pair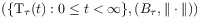 where
where 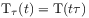 is a semigroup of operators
is a semigroup of operators
 mapping the Banach space
mapping the Banach space
 of functions
of functions 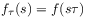 on
on 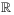 to itself.
[91.2.3] The argument
to itself.
[91.2.3] The argument 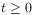 of
of 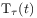 represents a time
duration, the argument
represents a time
duration, the argument 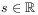 of
of 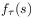 a
time instant.
[91.2.4] The index
a
time instant.
[91.2.4] The index 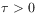 indicates the units (or scale) of time.
[91.2.5] Below,
indicates the units (or scale) of time.
[91.2.5] Below, 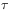 will again be frequently suppressed to simplify the notation.
[91.2.6] The elements
will again be frequently suppressed to simplify the notation.
[91.2.6] The elements 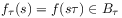 represent observables or
represent observables or[page 92, §0]
the state of a physical system as function of the time coordinate
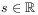 .
[92.0.1] The semigroup conditions require
.
[92.0.1] The semigroup conditions require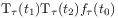
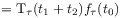
(7) 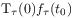
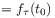
(8) for
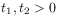 ,
, 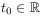 and
and 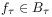 .
[92.0.2] The first condition may be viewed as representing the unlimited
divisibility of time.
.
[92.0.2] The first condition may be viewed as representing the unlimited
divisibility of time.
Continuity
[92.0.3] The time evolution is assumed to be strongly continuous in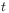 by demanding
by demanding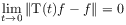
(9) for all
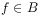 .
.Homogeneity
[92.0.4] The homogeneity of the time coordinate requires commutativity with translations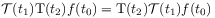
(10) for all
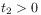 and
and 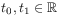 .
[92.0.5] This postulate allows to shift the origin of time
and it reflects the basic symmetry of time translation
invariance.
.
[92.0.5] This postulate allows to shift the origin of time
and it reflects the basic symmetry of time translation
invariance.Causality
[92.0.6] The time evolution operator should be causal in the sense that the function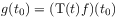 should depend only on values
of
should depend only on values
of 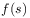 for
for 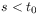 .
.Coarse Graining
[92.0.7] A time evolution operator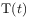 should be obtainable from
a coarse graining procedure.
[92.0.8] A precise definition of coarse graining is given in
Definition 2.3 below.
[92.0.9] The idea is to combine a time average
should be obtainable from
a coarse graining procedure.
[92.0.8] A precise definition of coarse graining is given in
Definition 2.3 below.
[92.0.9] The idea is to combine a time average
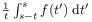 in the limit
in the limit 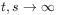 with a rescaling of
with a rescaling of 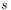 and
and 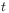 .
.
[92.0.10] While the first four requirements are conventional the fifth requires comment. [92.0.11] Averages over long intervals may themselves be timedependent on much longer time scales. [92.0.12] An example would be the position of an atom in a glass. [92.0.13] On short time scales the position fluctuates rapidly around a well defined average position. [92.0.14] On long time scales the structural relaxation processes in the glass can change this average position. [92.0.15] The purpose of any coarse graining procedure is to connect microscopic to macroscopic scales. [92.0.16] Of course, what is microscopic
[page 93, §0] depends on the physical situation. [93.0.1] Any microscopic time evolution may itself be viewed as macroscopic from the perspective of an underlying more microscopic theory. [93.0.2] Therefore it seems physically necessary and natural to demand that a time evolution should generally be obtainable from a coarse graining procedure.
2.2 Evolutions, Convolutions and Averages
[93.1.1] There is a close connection and mathematical similarity
between the simplest time evolution ![]() and
the operator
and
the operator ![]() of time averaging defined as
the mathematical mean
of time averaging defined as
the mathematical mean
| (11) |
where ![]() is the length of the averaging interval.
[93.1.2] Rewriting this formally as
is the length of the averaging interval.
[93.1.2] Rewriting this formally as
| (12) |
exhibits the relation between ![]() and
and ![]() .
[93.1.3] It shows also that
.
[93.1.3] It shows also that ![]() commutes with translations
(see eq. (10)).
commutes with translations
(see eq. (10)).
[93.2.1] A second even more suggestive relationship between ![]() and
and ![]() arises because
both operators can be written as convolutions.
[93.2.2] The operator
arises because
both operators can be written as convolutions.
[93.2.2] The operator ![]() may be written as
may be written as
| (13) |
where the kernel
| (14) |
is the characteristic function of the unit interval.
[93.2.3] The Laplace convolution in the last line requires ![]() .
[93.2.4] The translations
.
[93.2.4] The translations ![]() on the other hand may be
on the other hand may be
[page 94, §0] written as
| (15) |
where again ![]() is required for the Laplace convolution
in the last equation.
[94.0.1] The similarity between eqs. (15) and (13)
suggests to view the time translations
is required for the Laplace convolution
in the last equation.
[94.0.1] The similarity between eqs. (15) and (13)
suggests to view the time translations ![]() as a degenerate
form of averaging
as a degenerate
form of averaging ![]() over a single point.
[94.0.2] The operators
over a single point.
[94.0.2] The operators ![]() and
and ![]() are both convolution operators.
[94.0.3] By Lebesgues theorem
are both convolution operators.
[94.0.3] By Lebesgues theorem ![]() so that
so that ![]() in analogy with eq. (8) which holds for
in analogy with eq. (8) which holds for ![]() .
[94.0.4] However, while the translations
.
[94.0.4] However, while the translations ![]() fulfill eq. (7)
and form a convolution semigroup whose kernel
is the Dirac measure at 1,
the averaging operators
fulfill eq. (7)
and form a convolution semigroup whose kernel
is the Dirac measure at 1,
the averaging operators ![]() do not form a semigroup as will be
seen below.
do not form a semigroup as will be
seen below.
[94.1.1] The appearance of convolutions and convolution semigroups
is not accidental.
[94.1.2] Convolution operators arise quite generally from the symmetry
requirement of eq. (10) above.
[94.1.3] Let ![]() denote the Lebesgue spaces of
denote the Lebesgue spaces of
![]() -th power integrable functions, and let
-th power integrable functions, and let ![]() denote the Schwartz space of test functions for tempered
distributions [27].
[94.1.4] It is well established that all bounded linear operators
on
denote the Schwartz space of test functions for tempered
distributions [27].
[94.1.4] It is well established that all bounded linear operators
on ![]() commuting with translations (i.e.
fulfilling eq. (10)) are of convolution
type [27].
commuting with translations (i.e.
fulfilling eq. (10)) are of convolution
type [27].
Theorem 2.1
[94.1.5] Suppose the operator ![]() ,
, ![]() is linear, bounded and commutes with translations.
[94.1.6] Then there exists a unique tempered distribution
is linear, bounded and commutes with translations.
[94.1.6] Then there exists a unique tempered distribution ![]() such that
such that ![]() for all
for all ![]() .
.
[94.2.1] For ![]() the tempered distributions in this theorem
are finite Borel measures.
[94.2.2] If the measure is bounded and positive this means that
the operator B can be viewed as a weighted averaging
operator.
[94.2.3] In the following the case
the tempered distributions in this theorem
are finite Borel measures.
[94.2.2] If the measure is bounded and positive this means that
the operator B can be viewed as a weighted averaging
operator.
[94.2.3] In the following the case ![]() will be of interest.
[94.2.4] A positive bounded measure
will be of interest.
[94.2.4] A positive bounded measure ![]() on
on ![]() is uniquely determined by its distribution function
is uniquely determined by its distribution function
![]() defined by
defined by
| (16) |
[94.2.5] The tilde will again be omitted to simplify the notation.
[94.2.6] Physically a weighted average ![]() represents
the measurement of a signal
represents
the measurement of a signal ![]() using an apparatus
with response characterized by
using an apparatus
with response characterized by ![]() and resolution
and resolution ![]() .
[94.2.7] Note that the resolution (length of averaging interval) is a duration
and cannot be negative.
.
[94.2.7] Note that the resolution (length of averaging interval) is a duration
and cannot be negative.
[page 95, §1]
Definition 2.1 (Averaging)
[95.1.1] Let ![]() be a (probability) distribution function on
be a (probability) distribution function on ![]() , and
, and ![]() .
[95.1.2] The weighted (time) average of a function
.
[95.1.2] The weighted (time) average of a function ![]() on
on ![]() is
defined as the convolution
is
defined as the convolution
| (17) |
whenever it exists.
[95.1.3] The average is called causal if the support of ![]() is in
is in ![]() .
[95.1.4] It is called degenerate if the support of
.
[95.1.4] It is called degenerate if the support of ![]() consists of a single point.
consists of a single point.
[95.2.1] The weight function or kernel ![]() corresponding to a
distribution
corresponding to a
distribution ![]() is defined as
is defined as ![]() whenever
it exists.
whenever
it exists.
[95.3.1] The averaging operator ![]() in eq. (11)
corresponds to a measure with distribution function
in eq. (11)
corresponds to a measure with distribution function
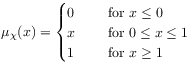 |
(18) |
while the time translation ![]() corresponds to the (Dirac) measure
corresponds to the (Dirac) measure
![]() concentrated at
concentrated at ![]() with distribution function
with distribution function
| (19) |
[95.3.2] Both averages are causal, and the latter is degenerate.
[95.4.1] Repeated averaging leads to convolutions.
[95.4.2] The convolution ![]() of two distributions
of two distributions ![]() on
on ![]() is
defined through
is
defined through
| (20) |
[95.4.3] The Fourier transform of a distribution is defined by
| (21) |
where the last equation holds when the distribution admits a
weight function.
[95.4.4] A sequence ![]() of distributions is said to
converge weakly to a limit
of distributions is said to
converge weakly to a limit ![]() ,
,
[page 96, §0] written as
| (22) |
if
| (23) |
holds for all bounded continuous functions ![]() .
.
[96.1.1] The operators ![]() and
and ![]() above have positive
kernels, and preserve positivity in the sense that
above have positive
kernels, and preserve positivity in the sense that
![]() implies
implies ![]() .
[96.1.2] For such operators one has
.
[96.1.2] For such operators one has
Theorem 2.2
[96.1.3] Let T be a bounded operator on ![]() ,
, ![]() that is translation invariant in the sense that
that is translation invariant in the sense that
| (24) |
for all ![]() and
and ![]() , and
such that
, and
such that ![]() and
and ![]() almost everywhere
implies
almost everywhere
implies ![]() almost everywhere.
[96.1.4] Then there exists a uniquely determined bounded measure
almost everywhere.
[96.1.4] Then there exists a uniquely determined bounded measure ![]() on
on ![]() with mass
with mass ![]() such that
such that
| (25) |
Proof.
[96.1.5] For the proof see [28]. ∎
[96.1.6] The preceding theorem suggests to represent those time evolutions that fulfill the requirements 1.– 4. of the last section in terms of convolution semigroups of measures.
Definition 2.2 (Convolution semigroup)
[96.1.7] A family ![]() of positive bounded measures on
of positive bounded measures on ![]() with the properties that
with the properties that
| (26) | |||
| (27) | |||
| (28) |
is called a convolution semigroup of measures on ![]() .
.
[page 97, §1]
[97.1.1] Here ![]() is the Dirac measure at
is the Dirac measure at ![]() and the limit is
the weak limit.
[97.1.2] The desired characterization of time evolutions now becomes
and the limit is
the weak limit.
[97.1.2] The desired characterization of time evolutions now becomes
Corollary 2.1
[97.1.3] Let ![]() be a strongly continuous time evolution
fulfilling the conditions of homogeneity and causality,
and being such that
be a strongly continuous time evolution
fulfilling the conditions of homogeneity and causality,
and being such that ![]() and
and ![]() almost everywhere implies
almost everywhere implies ![]() almost everywhere.
[97.1.4] Then
almost everywhere.
[97.1.4] Then ![]() corresponds uniquely to a convolution
semigroup of measures
corresponds uniquely to a convolution
semigroup of measures ![]() through
through
| (29) |
with ![]() for all
for all ![]() .
.
Proof.
[97.1.5] Follows from Theorem 2.2 and
the observation that ![]() would violate the causality condition.
∎
would violate the causality condition.
∎
2.3 Time Averaging and Coarse Graining
[97.3.1] The purpose of this section is to motivate the definition of coarse graining. [97.3.2] A first possible candidate for a coarse grained macroscopic time evolution could be obtained by simply rescaling the time in a microscopic time evolution as
| (30) |
where ![]() would be macroscopic times.
[97.3.3] However, apart from special cases,
the limit will in general not exist.
[97.3.4] Consider for example a sinusoidal
would be macroscopic times.
[97.3.3] However, apart from special cases,
the limit will in general not exist.
[97.3.4] Consider for example a sinusoidal ![]() oscillating
around a constant.
[97.3.5] Also, the infinite translation
oscillating
around a constant.
[97.3.5] Also, the infinite translation ![]() is
not an average, and this conflicts with the requirement
above, that coarse graining should be a smoothing operation.
is
not an average, and this conflicts with the requirement
above, that coarse graining should be a smoothing operation.
[97.4.1] A second highly popular candidate for coarse graining
is therefore the averaging operator ![]() .
[97.4.2] If the limit
.
[97.4.2] If the limit ![]() exists and
exists and ![]() is
integrable in the finite interval
is
integrable in the finite interval ![]() then
the average
then
the average
| (31) |
is a number independent of the instant ![]() .
[97.4.3] Thus, if one wants to study the macroscopic time dependence of
.
[97.4.3] Thus, if one wants to study the macroscopic time dependence of ![]() ,
it is necessary to consider a scaling limit in
,
it is necessary to consider a scaling limit in
[page 98, §0]
which also ![]() .
[98.0.1] If the scaling limit
.
[98.0.1] If the scaling limit ![]() is performed such that
is performed such that
![]() is constant, then
is constant, then
| (32) |
becomes again an averaging operator over the infinitely
rescaled observable.
[98.0.2] Now ![]() still does not qualify as a coarse grained
time evolution because
still does not qualify as a coarse grained
time evolution because ![]() as will be
shown next.
as will be
shown next.
[98.1.1] Consider again the operator ![]() defined
in eq. (11).
[98.1.2] It follows that
defined
in eq. (11).
[98.1.2] It follows that
| (33) |
and
![\frac{1}{t^{2}}\int^{x}_{0}\chi _{{[0,1]}}\left(\frac{x-y}{t}\right)\chi _{{[0,1]}}\left(\frac{y}{t}\right)\;\mbox{\rm d}y=\begin{cases}0&\text{\ \ \ \ for }x\leq 0\\
\frac{x}{t^{2}}&\text{\ \ \ \ for }0\leq x\leq t\\
\frac{2}{t}-\frac{x}{t^{2}}&\text{\ \ \ \ for }t\leq x\leq 2t\\
0&\text{\ \ \ \ for }x\geq 2t.\end{cases}](mi/mi45.png) |
(34) |
[98.1.3] Thus twofold averaging may be written as
| (35) |
where
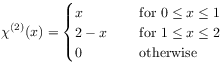 |
(36) |
is the new kernel.
[98.1.4] It follows that ![]() , and hence
the averaging operators
, and hence
the averaging operators ![]() do not form a semigroup.
do not form a semigroup.
[98.2.1] Although ![]() the iterated average is again
a convolution operator with support
the iterated average is again
a convolution operator with support ![]() compared
to
compared
to ![]() for
for ![]() .
[98.2.2] Similarly,
.
[98.2.2] Similarly, ![]() has support
has support ![]() .
[98.2.3] This suggests to investigate the iterated average
.
[98.2.3] This suggests to investigate the iterated average
![]() in a scaling limit
in a scaling limit ![]() .
[98.2.4] The limit
.
[98.2.4] The limit ![]() smoothes the function by
enlarging the
smoothes the function by
enlarging the
[page 99, §0]
averaging window to ![]() ,
and the limit
,
and the limit ![]() shifts the origin to infinity.
[99.0.1] The result may be viewed as a coarse grained time evolution
in the sense of a time evolution on time scales
"longer than infinitely long".
[99.0.2] c (This is a footnote:) c
The scaling limit was called "ultralong time limit" in [10]
It is therefore necessary to rescale
shifts the origin to infinity.
[99.0.1] The result may be viewed as a coarse grained time evolution
in the sense of a time evolution on time scales
"longer than infinitely long".
[99.0.2] c (This is a footnote:) c
The scaling limit was called "ultralong time limit" in [10]
It is therefore necessary to rescale ![]() .
[99.0.3] If the rescaling factor is called
.
[99.0.3] If the rescaling factor is called ![]() one is
interested in the limit
one is
interested in the limit ![]() with
with
![]() fixed, and
fixed, and ![]() with
with ![]() and fixed
and fixed ![]()
| (37) |
whenever this limit exists.
[99.0.4] Here ![]() denotes the macroscopic time.
denotes the macroscopic time.
[99.1.1] To evaluate the limit note first that eq. (11) implies
| (38) |
where ![]() denotes the rescaled observable
with a rescaling factor
denotes the rescaled observable
with a rescaling factor ![]() .
[99.1.2] The
.
[99.1.2] The ![]() -th iterated average may now be calculated by
Laplace transformation with respect to
-th iterated average may now be calculated by
Laplace transformation with respect to ![]() .
[99.1.3] Note that
.
[99.1.3] Note that
| (39) |
for all ![]() ,
where
,
where ![]() is the generalized Mittag-Leffler function defined as
is the generalized Mittag-Leffler function defined as
| (40) |
for all ![]() and
and ![]() .
[99.1.4] Using the general relation
.
[99.1.4] Using the general relation
| (41) |
| (42) |
where ![]() is the Laplace transform of
is the Laplace transform of ![]() .
[99.1.5] Noting that
.
[99.1.5] Noting that ![]() it becomes apparent that a
limit
it becomes apparent that a
limit ![]() will exist if the rescaling factors are
will exist if the rescaling factors are
[page 100, §0]
chosen as ![]() .
[100.0.1] With the choice
.
[100.0.1] With the choice ![]() and
and ![]() one finds
for the first factor
one finds
for the first factor
| (43) |
[100.0.2] Concerning the second factor assume that for each ![]() the limit
the limit
| (44) |
exists and defines a function ![]() .
[100.0.3] Then
.
[100.0.3] Then
| (45) |
and it follows that
| (46) |
[100.0.4] With ![]() Laplace inversion yields
Laplace inversion yields
| (47) |
[100.0.5] Using eq. (12) the result (47) may be expressed symbolically as
| (48) |
with ![]() .
[100.0.6] This expresses the macroscopic or coarse grained time evolution
.
[100.0.6] This expresses the macroscopic or coarse grained time evolution
![]() as the scaling limit of a
microscopic time evolution
as the scaling limit of a
microscopic time evolution ![]() .
[100.0.7] Note that there is some freedom in the choice of the
rescaling factors
.
[100.0.7] Note that there is some freedom in the choice of the
rescaling factors ![]() expressed by the prefactor
expressed by the prefactor ![]() .
[100.0.8] This freedom reflects the freedom to choose the time units
for the coarse grained time evolution.
.
[100.0.8] This freedom reflects the freedom to choose the time units
for the coarse grained time evolution.
[100.1.1] The coarse grained time evolution ![]() is again a translation.
[100.1.2] The coarse grained observable
is again a translation.
[100.1.2] The coarse grained observable ![]() corresponds
to a microscopic average by virtue
of the following result [29].
corresponds
to a microscopic average by virtue
of the following result [29].
[page 101, §1]
Proposition 2.1
[101.1.1] If ![]() is bounded from below and one of the limits
is bounded from below and one of the limits
or
exists then the other limit exists and
| (49) |
[101.1.2] Comparison of the last relation with eq. (44)
shows that ![]() is a microscopic average of
is a microscopic average of ![]() .
[101.1.3] While
.
[101.1.3] While ![]() is a microscopic time coordinate, the time coordinate
is a microscopic time coordinate, the time coordinate
![]() of
of ![]() is macroscopic.
is macroscopic.
[101.2.1] The preceding considerations justify to view the time evolution
![]() as a coarse grained time evolution.
[101.2.2] Every observation or measurement of a physical quantity
as a coarse grained time evolution.
[101.2.2] Every observation or measurement of a physical quantity
![]() requires a minimum duration
requires a minimum duration ![]() determined by the
temporal resolution of the measurement apparatus.
[101.2.3] The value
determined by the
temporal resolution of the measurement apparatus.
[101.2.3] The value ![]() at the time instant
at the time instant ![]() is always an average
over this minimum time interval.
[101.2.4] The averaging operator
is always an average
over this minimum time interval.
[101.2.4] The averaging operator ![]() with kernel
with kernel ![]() defined in equation (11) represents an
idealized averaging apparatus that can be switched on
and off instantaneously, and does not otherwise influence
the measurement.
[101.2.5] In practice one is usually confronted with finite startup
and shutdown times and a nonideal response of the apparatus.
[101.2.6] These imperfections are taken into account by using
a weighted average with a weight function or kernel
that differs from
defined in equation (11) represents an
idealized averaging apparatus that can be switched on
and off instantaneously, and does not otherwise influence
the measurement.
[101.2.5] In practice one is usually confronted with finite startup
and shutdown times and a nonideal response of the apparatus.
[101.2.6] These imperfections are taken into account by using
a weighted average with a weight function or kernel
that differs from ![]() .
[101.2.7] The weight function reflects conditions of the measurement, as well as
properties of the apparatus and its interaction with the system.
[101.2.8] It is therefore of interest to consider causal averaging operators
.
[101.2.7] The weight function reflects conditions of the measurement, as well as
properties of the apparatus and its interaction with the system.
[101.2.8] It is therefore of interest to consider causal averaging operators
![]() defined in eq. (17)
with general weight functions.
[101.2.9] A general coarse graining procedure is then
obtained from iterating these weighted averages.
defined in eq. (17)
with general weight functions.
[101.2.9] A general coarse graining procedure is then
obtained from iterating these weighted averages.
Definition 2.3 (Coarse Graining)
[101.2.10] Let ![]() be a probability distribution on
be a probability distribution on ![]() , and
, and
![]() ,
, ![]() a sequence of rescaling factors.
A coarse graining limit is defined as
a sequence of rescaling factors.
A coarse graining limit is defined as
| (50) |
[page 102, §0]
whenever the limit exists.
[102.0.1] The coarse graining limit is called causal if ![]() is causal, i.e. if
is causal, i.e. if ![]() .
.
2.4 Coarse Graining Limits and Stable Averages
[102.1.1] The purpose of this section is to investigate the coarse graining procedure introduced in Definition 2.3. [102.1.2] Because the coarse graining procedure is defined as a limit it is useful to recall the following well known result for limits of distribution functions [30]. [102.1.3] For the convenience of the reader its proof is reproduced in the appendix.
Proposition 2.2
[102.1.4] Let ![]() be a weakly convergent sequence of distribution functions.
[102.1.5] If
be a weakly convergent sequence of distribution functions.
[102.1.5] If ![]() , where
, where ![]() is nondegenerate
then for any choice of
is nondegenerate
then for any choice of ![]() and
and ![]() there exist
there exist ![]() and
and ![]() such that
such that
| (51) |
[102.2.1] The basic result for coarse graining limits can now be formulated.
Theorem 2.3 (Coarse Graining Limit)
[102.2.2] Let ![]() be such that the limit
be such that the limit ![]() defines the Fourier transform of a function
defines the Fourier transform of a function ![]() .
[102.2.3] Then the coarse graining limit exists and defines
a convolution operator
.
[102.2.3] Then the coarse graining limit exists and defines
a convolution operator
| (52) |
if and only if for any ![]() there are constants
there are constants ![]() and
and ![]() such that the distribution function
such that the distribution function ![]() obeys the
relation
obeys the
relation
| (53) |
Proof.
[102.2.4] In the previous section the coarse graining limit was evaluated
for the distribution ![]() from eq. (18) and
the corresponding
from eq. (18) and
the corresponding ![]() was found in eq. (47)
to be degenerate.
[102.2.5] A degenerate distribution
was found in eq. (47)
to be degenerate.
[102.2.5] A degenerate distribution ![]() trivially obeys eq. (53).
[102.2.6] Assume therefore from now on that neither
trivially obeys eq. (53).
[102.2.6] Assume therefore from now on that neither ![]() nor
nor ![]() are degenerate.
are degenerate.
[102.3.1] Employing equation (17) in the form
| (54) |
[page 103, §0]
one computes the Fourier transformation of ![]() with respect to
with respect to ![]()
| (55) |
[103.0.1] By assumption ![]() has a limit whenever
has a limit whenever ![]() with
with ![]() .
[103.0.2] Thus the coarse graining limit exists and is a convolution
operator whenever
.
[103.0.2] Thus the coarse graining limit exists and is a convolution
operator whenever ![]() converges
to
converges
to ![]() as
as ![]() .
[103.0.3] Following [30] it will be shown that this is true
if and only if the characterization (53)
and
.
[103.0.3] Following [30] it will be shown that this is true
if and only if the characterization (53)
and ![]() with
with ![]() apply.
[103.0.4] To see that
apply.
[103.0.4] To see that
| (56) |
holds, assume the contrary.
Then there is a subsequence ![]() converging to a finite
limit.
[103.0.5] Thus
converging to a finite
limit.
[103.0.5] Thus
| (57) |
so that
| (58) |
for all ![]() .
[103.0.6] As
.
[103.0.6] As ![]() this leads to
this leads to ![]() for all
for all ![]() and hence
and hence
![]() must be degenerate contrary to assumption.
must be degenerate contrary to assumption.
[103.1.1] Next, it will be shown that
| (59) |
[103.1.2] From eq. (56) it follows that
![]() and therefore
and therefore
| (60) |
and
| (61) |
Substituting ![]() by
by ![]() in
eq. (60) and by
in
eq. (60) and by ![]() in
eq. (61) shows that
in
eq. (61) shows that
| (62) |
[page 104, §0]
[104.0.1] If ![]() then there exists
a subsequence of either
then there exists
a subsequence of either ![]() or
or
![]() converging to a constant
converging to a constant ![]() .
[104.0.2] Therefore eq. (62) implies
.
[104.0.2] Therefore eq. (62) implies ![]() which upon iteration yields
which upon iteration yields
| (63) |
[104.0.3] Taking the limit ![]() then gives
then gives ![]() implying that
implying that ![]() is degenerate contrary to assumption.
is degenerate contrary to assumption.
[104.1.1] Now let ![]() be two constants.
[104.1.2] Because of (56) and (59)
it is possible to choose for each
be two constants.
[104.1.2] Because of (56) and (59)
it is possible to choose for each ![]() and
sufficiently large
and
sufficiently large ![]() an index
an index ![]() such that
such that
| (64) |
[104.1.3] Consider the identity
| (65) |
By hypothesis the distribution functions corresponding to
![]() converge to
converge to ![]() as
as ![]() .
[104.1.4] Hence each factor on the right hand side converges and
their product converges to
.
[104.1.4] Hence each factor on the right hand side converges and
their product converges to ![]() .
[104.1.5] It follows that the distribution function on the
left hand side must also converge.
[104.1.6] By Proposition 2.2 there must exist
.
[104.1.5] It follows that the distribution function on the
left hand side must also converge.
[104.1.6] By Proposition 2.2 there must exist ![]() and
and
![]() such that the left hand side differs from
such that the left hand side differs from ![]() only as
only as ![]() .
.
[104.2.1] Finally the converse direction that the coarse graining
limit exists for ![]() is seen to follow from
eq. (53).
[104.2.2] This concludes the proof of the theorem.
∎
is seen to follow from
eq. (53).
[104.2.2] This concludes the proof of the theorem.
∎
[104.3.1] The theorem shows that the coarse graining limit, if it
exists, is again a macroscopic weighted average ![]() .
[104.3.2] The condition (53) says that this macroscopic average
has a kernel that is stable under convolutions, and this motivates the
.
[104.3.2] The condition (53) says that this macroscopic average
has a kernel that is stable under convolutions, and this motivates the
Definition 2.4 (Stable Averages)
[104.3.3] A weighted averaging operator ![]() is called stable
if for any
is called stable
if for any ![]() there are constants
there are constants ![]() and
and ![]() such that
such that
| (66) |
holds.
[104.4.1] This nomenclature emphasizes the close relation with the limit theorems of probability theory [30, 31]. [104.4.2] The next theorem provides the explicit form for distribution functions satisfying eq. (66). [104.4.3] The proof uses Bernsteins theorem and hence requires the concept of complete monotonicity.
[page 105, §1]
Definition 2.5
[105.1.1] A ![]() -function
-function ![]() is called
completely monotone if
is called
completely monotone if
| (67) |
for all integers ![]() .
.
[105.2.1] Bernsteins theorem [31, p. 439] states that a function
is completely monotone if and only if it is the the
Laplace transform (![]() )
)
| (68) |
of a distribution ![]() or of a density
or of a density ![]() .
.
[105.3.1] In the next theorem the explicit form of stable averaging kernels
is found to be a special case of the general ![]() -function.
[105.3.2] Because the
-function.
[105.3.2] Because the ![]() -function will reappear in other results
its general definition and properties
are presented separately in Section 4.
-function will reappear in other results
its general definition and properties
are presented separately in Section 4.
Theorem 2.4
[105.3.3] A causal average is stable if and only if its weight function is of the form
| (69) |
where ![]() ,
, ![]() and
and ![]() are constants
and
are constants
and ![]() .
.
Proof.
[105.3.4] Let ![]() without loss of generality.
[105.3.5] The condition (66) together with
without loss of generality.
[105.3.5] The condition (66) together with
![]() defines one sided
stable distribution functions [31].
[105.3.6] To derive the form (69) it suffices to consider
condition (66) with
defines one sided
stable distribution functions [31].
[105.3.6] To derive the form (69) it suffices to consider
condition (66) with ![]() .
[105.3.7] Assume thence that for any
.
[105.3.7] Assume thence that for any ![]() there exists
there exists ![]() such that
such that
| (70) |
where the convolution is now a Laplace convolution
because of the condition ![]() .
[105.3.8] Laplace tranformation yields
.
[105.3.8] Laplace tranformation yields
| (71) |
[105.3.9] Iterating this equation (with ![]() ) shows that
there is an
) shows that
there is an ![]() -dependent constant
-dependent constant ![]() such that
such that
| (72) |
[page 106, §0] and hence
| (73) |
[106.0.1] Thus ![]() satisfies the functional equation
satisfies the functional equation
| (74) |
whose solution is ![]() with some real constant
written as
with some real constant
written as ![]() with hindsight.
[106.0.2] Inserting
with hindsight.
[106.0.2] Inserting ![]() into eq.(72) and substituting
the function
into eq.(72) and substituting
the function ![]() gives
gives
| (75) |
[106.0.3] Taking logarithms and substituting ![]() this becomes
this becomes
| (76) |
[106.0.4] The solution to this functional equation is ![]() .
[106.0.5] Substituting back one finds
.
[106.0.5] Substituting back one finds ![]() and therefore
and therefore
![]() is of the general form
is of the general form ![]() with
with ![]() .
[106.0.6] Now
.
[106.0.6] Now ![]() is also a distribution function. Its normalization
requires
is also a distribution function. Its normalization
requires ![]() and this restricts
and this restricts ![]() to
to ![]() .
[106.0.7] Moreover, by Bernsteins theorem
.
[106.0.7] Moreover, by Bernsteins theorem ![]() must be completely
monotone.
[106.0.8] A completely monotone function is positive, decreasing
and convex.
[106.0.9] Therefore the power in the exponent
must have a negative prefactor, and
the exponent is restricted to the range
must be completely
monotone.
[106.0.8] A completely monotone function is positive, decreasing
and convex.
[106.0.9] Therefore the power in the exponent
must have a negative prefactor, and
the exponent is restricted to the range ![]() .
[106.0.10] Summarizing, the Laplace transform
.
[106.0.10] Summarizing, the Laplace transform ![]() of a distribution
satisfying (70) is of the form
of a distribution
satisfying (70) is of the form
| (77) |
with ![]() and
and ![]() .
[106.0.11] Checking that
.
[106.0.11] Checking that ![]() does indeed satisfy
eq. (70) yields
does indeed satisfy
eq. (70) yields ![]() as the relation between the constants.
[106.0.12] For the proof of the general case of eq. (66)
see Refs. [30, 31].
as the relation between the constants.
[106.0.12] For the proof of the general case of eq. (66)
see Refs. [30, 31].
[106.1.1] To invert the Laplace transform it is convenient to use the relation
| (78) |
between the Laplace transform and the Mellin transform
| (79) |
[107.0.4] Note that ![]() is the standardized form
used in eq. (5).
[107.0.5] It remains to investigate the sequence of rescaling factors
is the standardized form
used in eq. (5).
[107.0.5] It remains to investigate the sequence of rescaling factors ![]() .
[107.0.6] For these one finds
.
[107.0.6] For these one finds
Corollary 2.2
[107.0.7] If the coarse graining limit exists and is nondegenerate
then the sequence ![]() of rescaling factors has the
form
of rescaling factors has the
form
| (84) |
where ![]() and
and ![]() is slowly varying,
i.e.
is slowly varying,
i.e. ![]() for all
for all ![]() (see
Chapter IX, Section 2.3).
(see
Chapter IX, Section 2.3).
Proof.
[33][107.0.8] Let ![]() .
[107.0.9] Then for all
.
[107.0.9] Then for all ![]() and any fixed
and any fixed ![]()
| (85) |
[107.0.10] On the other hand
| (86) |
where the remainder tends uniformly to zero on every
finite interval.
[107.0.11] Suppose that the sequence ![]() is unbounded
so that there is a subsequence with
is unbounded
so that there is a subsequence with ![]() .
[107.0.12] Setting
.
[107.0.12] Setting ![]() in eq. (86) and using
eq. (85) gives
in eq. (86) and using
eq. (85) gives
[page 108, §0]
![]() which cannot be satisfied
because
which cannot be satisfied
because ![]() .
[108.0.1] Hence
.
[108.0.1] Hence ![]() is bounded.
[108.0.2] Now the limit
is bounded.
[108.0.2] Now the limit ![]() in eqs. (85) and (86) gives
in eqs. (85) and (86) gives
| (87) |
[108.0.3] This requires that
| (88) |
implying eq. (84) by virtue of the Characterization Theorem 2.2 in Chapter IX. [108.0.4] (For more information on slow and regular variation see Chapter IX and references therein). ∎
2.5 Macroscopic Time Evolutions
[108.1.1] The preceding results show that a coarse graining limit is
characterized by the quantities ![]() .
[108.1.2] These quantities are determined by the coarsening weight
.
[108.1.2] These quantities are determined by the coarsening weight ![]() .
[108.1.3] The following result, whose proof can be found in
[33, p. 85], gives their relation with the
coarsening weight.
.
[108.1.3] The following result, whose proof can be found in
[33, p. 85], gives their relation with the
coarsening weight.
Theorem 2.5 (Universality Classes of Time Evolutions)
[108.1.4] In order that a causal coarse graining limit based on ![]() gives rise to a macroscopic average with
gives rise to a macroscopic average with ![]() it is necessary and sufficient that
it is necessary and sufficient that ![]() behaves as
behaves as
| (89) |
in a neighbourhood of ![]() , and that
, and that ![]() is slowly
varying for
is slowly
varying for ![]() .
[108.1.5] In case
.
[108.1.5] In case ![]() the rescaling factors can be chosen as
the rescaling factors can be chosen as
| (90) |
while the case ![]() reduces to the degenerate case
reduces to the degenerate case ![]() .
.
[108.2.1] The preceding theorem characterizes the domain of attraction of a universality class of time evolutions. [108.2.2] Summarizing the results gives a characterization of macroscopic time evolutions arising from coarse graining limits.
Theorem 2.6 (Macroscopic Time Evolution)
[108.2.3] Let ![]() be such that the limit
be such that the limit ![]() defines the Fourier transform of a function
defines the Fourier transform of a function ![]() .
[108.2.4] If
.
[108.2.4] If ![]() is a causal average whose coarse graining limit
exists with
is a causal average whose coarse graining limit
exists with ![]() as
as
[page 109, §0] in the preceding theorem then
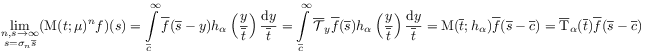 |
(91) |
defines a family of one parameter semigroups ![]() with
parameter
with
parameter ![]() indexed by
indexed by ![]() .
[109.0.1] Here
.
[109.0.1] Here ![]() denotes the translation
semigroup, and
denotes the translation
semigroup, and ![]() is a constant.
is a constant.
Proof.
[109.0.2] Noting that ![]() and
combining Theorems 2.3 and 2.4 gives
and
combining Theorems 2.3 and 2.4 gives
| (92) |
where ![]() ,
, ![]() and
and ![]() are the constants from
theorem 2.4 and the last equality defines the operators
are the constants from
theorem 2.4 and the last equality defines the operators
![]() with
with ![]() and
and ![]() .
[109.0.3] Fourier transformation then yields
.
[109.0.3] Fourier transformation then yields
| (93) |
and the semigroup property (7) follows from
| (94) |
by Fourier inversion. [109.0.4] Condition (8) is checked similarly. ∎
[109.0.5] The family of semigroups ![]() indexed by
indexed by ![]() that can arise from coarse graining limits are called
macroscopic time evolutions.
[109.0.6] These semigroups are also holomorphic, strongly continuous
and equibounded (see Chapter III).
that can arise from coarse graining limits are called
macroscopic time evolutions.
[109.0.6] These semigroups are also holomorphic, strongly continuous
and equibounded (see Chapter III).
[109.1.1] From a physical point of view this
result emphasizes the different role
played by ![]() and
and ![]() .
[109.1.2] While
.
[109.1.2] While ![]() is the
macroscopic time coordinate whose values are
is the
macroscopic time coordinate whose values are
![]() , the duration
, the duration ![]() is positive.
[109.1.3] If the dimension of a microscopic time duration
is positive.
[109.1.3] If the dimension of a microscopic time duration ![]() is [s], then
the dimension of the macroscopic time duration
is [s], then
the dimension of the macroscopic time duration ![]() is [s
is [s![]() ].
].
[page 110, §1]
2.6 Infinitesimal Generators
[110.1.1] The importance of the semigroups ![]() for
theoretical physics as universal attractors of coarse
grained macroscopic time evolutions seems not to have
been noticed thus far.
[110.1.2] This is the more surprising as their mathematical
importance for harmonic analysis and probability
theory has long been recognized [31, 34, 35, 28].
[110.1.3] The infinitesimal generators are known
to be fractional derivatives [31, 35, 36, 37].
[110.1.4] The infinitesimal generators are defined as
for
theoretical physics as universal attractors of coarse
grained macroscopic time evolutions seems not to have
been noticed thus far.
[110.1.2] This is the more surprising as their mathematical
importance for harmonic analysis and probability
theory has long been recognized [31, 34, 35, 28].
[110.1.3] The infinitesimal generators are known
to be fractional derivatives [31, 35, 36, 37].
[110.1.4] The infinitesimal generators are defined as
| (95) |
[110.1.5] For more details on semigroups and their infinitesimal generators see Chapter III.
[110.2.1] Formally one calculates ![]() by applying direct and
inverse Laplace transformation
with
by applying direct and
inverse Laplace transformation
with ![]() in eq. (91) and using eq. (77)
in eq. (91) and using eq. (77)
| (96) |
[110.2.2] The result can indeed be made rigorous and one has
Theorem 2.7
[110.2.3] The infinitesimal generator ![]() of the macroscopic
time evolutions
of the macroscopic
time evolutions ![]() is related to the infinitesimal
generator
is related to the infinitesimal
generator ![]() of
of ![]() through
through
| (97) |
Proof.
See Chapter III. ∎
[page 111, §1]
[111.1.1] The theorem shows that fractional derivatives
of Marchaud type arise as the infinitesimal
generators of coarse grained time evolutions in physics.
[111.1.2] The order ![]() of the derivative lies between zero and unity,
and it is determined by the decay of the averaging kernel.
[111.1.3] The order
of the derivative lies between zero and unity,
and it is determined by the decay of the averaging kernel.
[111.1.3] The order ![]() gives a quantitative measure for the decay of the
averaging kernel.
[111.1.4] The case
gives a quantitative measure for the decay of the
averaging kernel.
[111.1.4] The case ![]() indicates that memory effects and history
dependence may become important.
indicates that memory effects and history
dependence may become important.
