Hierbei stellen sich allerdings zwei Fragen:
Wie berechnet man eigentlich ![]() ?
Und wie geht man vor, wenn die analytische Lösung nicht
einfach eine harmonische Schwingung (oder sonst eine
``elementare'' Funktion) ist ?
?
Und wie geht man vor, wenn die analytische Lösung nicht
einfach eine harmonische Schwingung (oder sonst eine
``elementare'' Funktion) ist ?
Um die Fragen zu beantworten ist es erforderlich sich an
die mathematische Definition von ![]() zu erinnern.
Es gibt viele Definitionen.
Eine der Definitionen von
zu erinnern.
Es gibt viele Definitionen.
Eine der Definitionen von ![]() lautet: Die
trigonometrische Funktion
lautet: Die
trigonometrische Funktion ![]() ist diejenige
Funktion
ist diejenige
Funktion ![]() , welche die Gleichung
, welche die Gleichung
![]() mit
Anfangsbedingungen
mit
Anfangsbedingungen ![]() und
und
![]() löst.
Das ist aber gerade unsere Differentialgleichung
(
löst.
Das ist aber gerade unsere Differentialgleichung
(![]() ) mit
) mit ![]() !
Diese Definition ist nutzlos weil zirkulär.
Die Katze beisst sich selbst in den Schwanz.
Um die Lösung zu berechnen muss man die Kosinusfunktion
berechnen können, und um die Kosinusfuinktion berechnen
zu können muss man die Lösung berechnen können.
So kommen wir also nicht weiter.
!
Diese Definition ist nutzlos weil zirkulär.
Die Katze beisst sich selbst in den Schwanz.
Um die Lösung zu berechnen muss man die Kosinusfunktion
berechnen können, und um die Kosinusfuinktion berechnen
zu können muss man die Lösung berechnen können.
So kommen wir also nicht weiter.
Die vielleicht bekannteste Definition von ![]() ist
die Entwicklung in eine Potenzreihe
ist
die Entwicklung in eine Potenzreihe
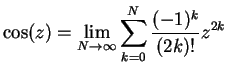 |
(1.18) |
Das Problem wird klarer, wenn man etwa statt der einfachen Gleichung für den harmonischen Oszillator mit der nur leicht abgeänderten Gleichung
| (1.19) |
Wir wollen uns deshalb auf den Standpunkt stellen,
dass die benutzte Programmiersprache keine fertigen
Funktionen für ![]() und
und ![]() bereitstellt,
und wir sie deshalb selbst berechnen müssen.
bereitstellt,
und wir sie deshalb selbst berechnen müssen.