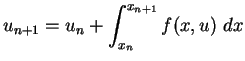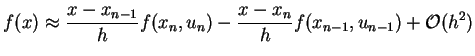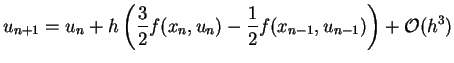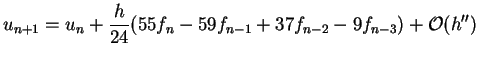Next: Implizite Verfahren
Up: Numerische Lösungsverfahren
Previous: Runge-Kutta-Verfahren
Eine allgemeine Methode die Genauigkeit zu erhöhen besteht
darin, dass man 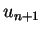 nicht nur aus
nicht nur aus 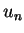 berechnet, sondern
aus mehreren Werten
berechnet, sondern
aus mehreren Werten
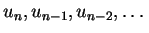 aus der
Vergangenheit.
Ausgangspunkt ist wieder die exakte Gleichung (
aus der
Vergangenheit.
Ausgangspunkt ist wieder die exakte Gleichung (![[*]](file:/mnt/bison/local/lib/latex2html/icons/crossref.gif) )
)
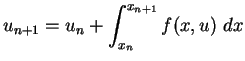 |
(5.53) |
Da 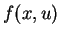 im Intervall
im Intervall
![$ [x_n , x_{n+1}]$](img519.gif) nicht bekannt ist
extrapoliert man linear vom Intervall
nicht bekannt ist
extrapoliert man linear vom Intervall
![$ [x_{n-1}, x_{n}]$](img540.gif) und schreibt:
und schreibt:
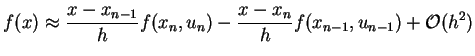 |
(5.54) |
setzt man dies in (![[*]](file:/mnt/bison/local/lib/latex2html/icons/crossref.gif) ) ein und integriert so erhält
man das Zweischrittverfahren von Adams-Bashforth
) ein und integriert so erhält
man das Zweischrittverfahren von Adams-Bashforth
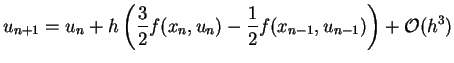 |
(5.55) |
Verfahren höherer Ordnung erhält man, indem man mit Polynomen
höherer Ordnung aus dem früheren Intervallen extrapoliert.
Eine 4-Schrittmethode nach Adams -Bashforth lautet
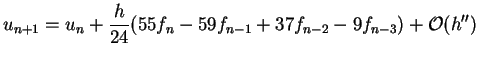 |
(5.56) |
wobei
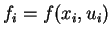 ist.
ist.
© R.Hilfer et al., ICA-1, Univ. Stuttgart
28.6.2002