



Next: Prädiktor-Korrektor-Verfahren
Up: Numerische Lösungsverfahren
Previous: Mehrschrittverfahren(Adams-Bashforth)
Alle bisher diskutierten Verfahren waren explizit. Das bedeutet,
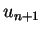 hängt nur von
hängt nur von 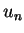 oder
oder 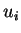 mit
mit 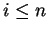 ab. Also
formal
ab. Also
formal
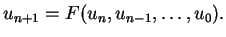 |
(5.57) |
Bei impliziten Verfahren tritt dagegen auf der rechten Seite
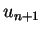 auf
auf
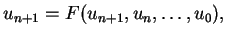 |
(5.58) |
so dass eine nichtlineare Gleichung gelöst
werden muss (z.B. durch Iteration).
Wir betrachten wieder die Gleichung
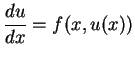 |
(5.59) |
an der Stelle
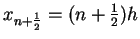 zwischen
zwei Stützpunkten. Also
zwischen
zwei Stützpunkten. Also
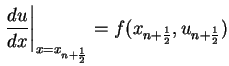 |
(5.60) |
Wir setzen jetzt für
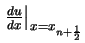 die
symmetrische Differenz
die
symmetrische Differenz
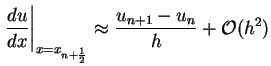 |
(5.61) |
und für
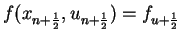 setzen wir näherugsweise
setzen wir näherugsweise
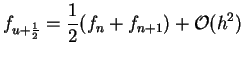 |
(5.62) |
den Mittelwert. Dann folgt
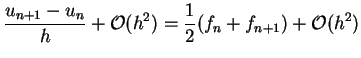 |
(5.63) |
oder
![$\displaystyle u_{n+1}=u_n+\frac{h}{2}[f(x_n,u_n)+f(x_{n+1},u_{n+1})]+{\cal O}(h^3)$](img554.gif) |
(5.64) |
Dies ist alles sehr schön, aber die Lösung dieser impliziten
Gleichung ist numerisch aufwendig. Deshalb werden diese Methoden
in der Praxis wenig verwendet, wenn man von Prädiktor-Konektor-Methoden
(s.u.) absieht.
Ausserdem ist manchmal 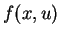 linear in
linear in 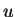 , d.h.
, d.h.
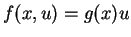 . Dann wäre (
. Dann wäre (![[*]](file:/mnt/bison/local/lib/latex2html/icons/crossref.gif) )
lösbar.
)
lösbar.




Next: Prädiktor-Korrektor-Verfahren
Up: Numerische Lösungsverfahren
Previous: Mehrschrittverfahren(Adams-Bashforth)
© R.Hilfer et al., ICA-1, Univ. Stuttgart
28.6.2002
![]() hängt nur von
hängt nur von ![]() oder
oder ![]() mit
mit ![]() ab. Also
formal
ab. Also
formal
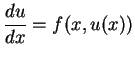
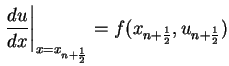
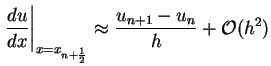
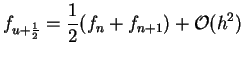
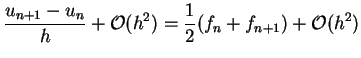
![]() linear in
linear in ![]() , d.h.
, d.h.
![]() . Dann wäre (
. Dann wäre (![]() )
lösbar.
)
lösbar.