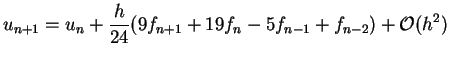Next: Himmelsmechanik
Up: Numerische Lösungsverfahren
Previous: Implizite Verfahren
Die Idee dieser Verfahren besteht darin, mit einem expliziten
Verfahren einen Prädiktor 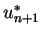 für
für 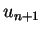 zu
schätzen, und dann diesen Schätzwert auf der rechten Seite
eines implizierten Mehrschrittverfahrens zu benutzen, um den
korrigierten Wert (Korrektor)
zu
schätzen, und dann diesen Schätzwert auf der rechten Seite
eines implizierten Mehrschrittverfahrens zu benutzen, um den
korrigierten Wert (Korrektor) 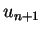 zu berechnen, der dann
in den nächsten Schritt eingeht.
Ein Beispiel ist das implizite Adams-Moulton-Verfahren mit der
Formel
zu berechnen, der dann
in den nächsten Schritt eingeht.
Ein Beispiel ist das implizite Adams-Moulton-Verfahren mit der
Formel
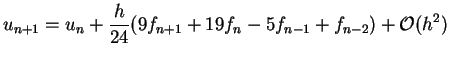 |
(5.65) |
wobei wieder
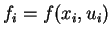 bedeutet.
Dies ist ein implizites Dreischrittverfahren (weil die drei Werte
bedeutet.
Dies ist ein implizites Dreischrittverfahren (weil die drei Werte
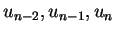 den Wert
den Wert 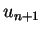 bestimmen.)
bestimmen.)
Kombiniert mit dem Adams-Bashforth-Verfahren ergibt sich die
Prädiktor-Korektor-Methode
Dieses Vorgehen (beachte 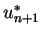 in (
in (![[*]](file:/mnt/bison/local/lib/latex2html/icons/crossref.gif) )) heißt auch
Adams-Bashforth-Moulton-Methode.Es ist
)) heißt auch
Adams-Bashforth-Moulton-Methode.Es ist
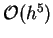 hat aber den Vorteil,
dass man mit Hilfe der Differenz
hat aber den Vorteil,
dass man mit Hilfe der Differenz
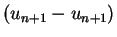 ständig die
Fehler der Integration beobachten kann.
ständig die
Fehler der Integration beobachten kann.
© R.Hilfer et al., ICA-1, Univ. Stuttgart
28.6.2002