Ein Beispiel für die Anwendung der Relativitätstheorie in der
Himmelsmechanik ist die Präzession des Perihels (der Umlaufbahn)
des Merkurs, die aufgrund seiner Sonnennähe relativ groß ist.
Die Bahn des Merkurs dreht sich um 566 Arksek/Jahrhundert
(1 Arksek = (1/3600)![]() ). Für eine volle Umdrehung benötigt die
Bahn insgesamt 230000 Jahre!
Wird die Präzession allerdings selbst mit dem Einfluß des
Jupiters errechnet, kommt man nur auf 523 Arksek/Jahrhundert! Albert Einstein
erhält durch seine Allgemeine Relativitätstheorie (Raum wird durch Masse
gekrümmt) ein erweitertes
Bewegungsgesetz. Für die Kraft zwischen Sonne und Merkur gilt nun:
). Für eine volle Umdrehung benötigt die
Bahn insgesamt 230000 Jahre!
Wird die Präzession allerdings selbst mit dem Einfluß des
Jupiters errechnet, kommt man nur auf 523 Arksek/Jahrhundert! Albert Einstein
erhält durch seine Allgemeine Relativitätstheorie (Raum wird durch Masse
gekrümmt) ein erweitertes
Bewegungsgesetz. Für die Kraft zwischen Sonne und Merkur gilt nun:
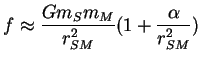 , mit , mit |
(5.75) |