



Next: Weitere Vielteilchensysteme
Up: Molekulardynamik
Previous: Das Heliumatom
Durch die gegenseitige Wechselwirkung ist der Aufwand bei 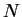 Teilchen
Teilchen
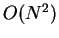 , da der Einfluß von allen Teilchen auf jedes Teilchen berücksichtigt
wird. Nun ist es aber so, daß die Stärke der Kraft von der Entfernung der
Teilchen abhängt. Nur die Teilchen in näherer Umgebung haben einen wirklichen
Einfluß auf die Bewegung. Um das auszunutzen gibt es verschiedene Ansätze:
, da der Einfluß von allen Teilchen auf jedes Teilchen berücksichtigt
wird. Nun ist es aber so, daß die Stärke der Kraft von der Entfernung der
Teilchen abhängt. Nur die Teilchen in näherer Umgebung haben einen wirklichen
Einfluß auf die Bewegung. Um das auszunutzen gibt es verschiedene Ansätze:
- Nachbarschaftstafeln
Für jedes Teilchen 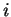 gibt es eine Liste von Teilchen die sich innerhalb einer
Kugel (oder eines Kreises) mit dem Radius
gibt es eine Liste von Teilchen die sich innerhalb einer
Kugel (oder eines Kreises) mit dem Radius 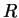 um Teilchen
um Teilchen 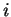 befinden.
befinden.
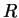 muß dabei größer als die Reichweite der Kräfte sein.
Für das Teilchen
muß dabei größer als die Reichweite der Kräfte sein.
Für das Teilchen 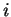 werden nur die Kräfte aus den in der Liste stehenden
Teilchen berechnet und die Liste wird regelmäßig erneuert. Der Erneuerungsprozeß
kann zwar
werden nur die Kräfte aus den in der Liste stehenden
Teilchen berechnet und die Liste wird regelmäßig erneuert. Der Erneuerungsprozeß
kann zwar 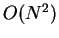 sein, aber der Aufwand muß nur nach vielen Zeitschritten
betrieben werden.
sein, aber der Aufwand muß nur nach vielen Zeitschritten
betrieben werden.
- linked-cell (verbundene Zellen)
Der Raum (die Ebene) wird in einzelne Zellen unterteilt. Jede Zelle
besitzt eine Liste der Teilchen in ihr und jedes Teilchen in einer Zelle
wechselwirkt nur mit Teilchen in umgebenden Zellen. Für die Berechnung werden
nur die Teilchen aus der eigenen und den benachbarten Zellen herangezogen.
Abbildung:
Verlet-Nachbarschaftstafeln (oben) und linked-cell (unten)
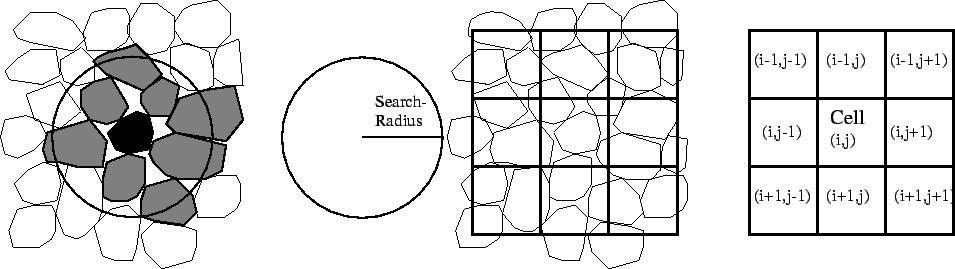 |
Durch Kombination dieser beiden Methoden kann man einen Aufwand von 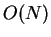 erreichen. Außerdem lassen sich die Methoden sehr einfach parallelisieren
und so auch auf Systemen mit mehreren Recheneinheiten effektiv realisieren.
erreichen. Außerdem lassen sich die Methoden sehr einfach parallelisieren
und so auch auf Systemen mit mehreren Recheneinheiten effektiv realisieren.




Next: Weitere Vielteilchensysteme
Up: Molekulardynamik
Previous: Das Heliumatom
© R.Hilfer et al., ICA-1, Univ. Stuttgart
28.6.2002
![]() Teilchen
Teilchen
![]() , da der Einfluß von allen Teilchen auf jedes Teilchen berücksichtigt
wird. Nun ist es aber so, daß die Stärke der Kraft von der Entfernung der
Teilchen abhängt. Nur die Teilchen in näherer Umgebung haben einen wirklichen
Einfluß auf die Bewegung. Um das auszunutzen gibt es verschiedene Ansätze:
, da der Einfluß von allen Teilchen auf jedes Teilchen berücksichtigt
wird. Nun ist es aber so, daß die Stärke der Kraft von der Entfernung der
Teilchen abhängt. Nur die Teilchen in näherer Umgebung haben einen wirklichen
Einfluß auf die Bewegung. Um das auszunutzen gibt es verschiedene Ansätze:
![]() erreichen. Außerdem lassen sich die Methoden sehr einfach parallelisieren
und so auch auf Systemen mit mehreren Recheneinheiten effektiv realisieren.
erreichen. Außerdem lassen sich die Methoden sehr einfach parallelisieren
und so auch auf Systemen mit mehreren Recheneinheiten effektiv realisieren.