Computerformulierung

Bis jetzt wurde die Hilfe des Computers noch nicht benötigt. Außerdem wäre es möglich die numerischen Algorithmen (() oder ()) mit Hilfe eines Taschenrechners durchzuführen (oder auch wie im letzten Jahrhundert mit Papier und Bleistift), und die Ergebnisse auf Millimeterpapier zu übertragen. Das wäre allerdings sehr arbeitsaufwendig.

Wir wollen deshalb ein Computerprogramm zu schreiben, welches uns die Arbeit abnimmt und die gesuchte Lösung $u(s)$ für die Auslenkungen des Federpendels an den Stützstellen $s=n\Delta s$ mit $\Delta s=0,1$ und $n=0,1,2,...,20$ berechnet. Wie man das Computerprogramm schreibt werden wir im nächsten Kapitel besprechen, und es gibt immer mehr als eine Lösung. Eine mögliche Implementierung unseres numerischen Algorithmus wäre das folgende Programm in C++. Wir betonen, daß  das nachfolgende Programm in sehr ``schlechtem'' Stil geschrieben ist. Warum ist weiter unten im Abschnitt erklärt.

#include<iostream>
#include<fstream>
int main()
{
   double u[2], v[2], t; 
   double C,omega;       
   double u_0,v_0;       
   double t_max, dt;     
   cout << "dimensionslose Frequenz :";  cin >> omega;
   cout << "Anfangsauslenkung       :";  cin >> u_0;
   cout << "Anfangsgeschwindigkeit  :";  cin >> v_0;
   cout << "Gesamtzeit     :";  cin >> t_max;
   cout << "Zeitintervall  :";  cin >> dt;
   C = omega*omega;      
   u[0]=u_0;             
   v[0]=v_0;
   t=0.0;
   ofstream outfile("harmos.dat"); 
   for( int i=0; i<=t_max/dt; i++ )
   {
     v[1]=v[0]-C*u[0]*dt;
     u[1]=u[0]+v[1]*dt;       
     outfile << t << "\t" << u[0] << "\t" << u_0*cos(omega*t) << "\n";
     t=t+dt;              
     u[0]=u[1];           
     v[0]=v[1];
   }
}

Die Bedeutung der vielen Symbole wird in den folgenden Kapiteln ausführlicher erklärt werden. Zum Schreiben des Programms benützt man einen Editor (Textverarbeitung) wie z.B. xedit, emacs oder xemacs. Das geschriebene Programm kann man dann als Datei harmon.cc abspeichern, wobei die Endung .cc anzeigt daß es sich um ein C++ Programm handelt. Der Computer kann mit der angelegten Datei alleine noch nichts anfangen. Man muß  die Datei erst in Maschinensprache übersetzen. Dieses Übersetzen nennt man auch Kompilieren. Das Kompilieren geschieht mit dem Kommando

 g++ harmos.cc -o harmos,

welches die ausführbare Datei harmos erzeugt. Diese Datei wird durch Eingeabe des Kommando harmos aktiviert und fragt dann nacheinander die Parameter, die Gesamtzeit und das Zeitintervall der Stützstellen ab. Hat man diese eingegeben, so erzeugt das Programm die Datei harmos.dat, mit z.B. folgendem Inhalt (bei Verwendung von Gesamtdauer tmax=2.0 und Zeitschritt dt=0.1):

0       1       1
0.1     0.91    0.955336
0.2     0.7381  0.825336
0.3     0.499771        0.62161
0.4     0.216463        0.362358
0.5     -0.0863274      0.0707372
0.6     -0.381348       -0.227202
0.7     -0.642047       -0.504846
0.8     -0.844962       -0.737394
0.9     -0.971831       -0.904072
1       -1.01123        -0.989992
1.1     -0.959627       -0.98748
1.2     -0.821653       -0.896758
1.3     -0.60973        -0.725932
1.4     -0.342932       -0.490261
1.5     -0.0452697      -0.210796
1.6     0.256467        0.087499
1.7     0.535121        0.377978
1.8     0.765615        0.634693
1.9     0.927203        0.834713

Die erste Spalte entält die Zeitpunkte. Die zweite Spalte enthält die mit dem numerischen Algorithmus () berechnet worden sind. Die letzte Zeile ist das Ergebnis der ``numerisch exakten'' Auswertung der Lösungsformel in (), welche einfach mit Hilfe in C++ vorhandenen Kosinusfunktion berechnet wurde. Man sieht deutlich, daß  die Werte verschieden sind. Dies liegt an der Wahl von $\Delta s=0.1$ Für $\Delta s\to 0$ nähern sich die Werte einander an. Man überzeuge sich davon.

Abbildung: Graphische Darstellung der Lösung auf dem Bildschirm. Die Symbole (+) markieren die iterativ gewonnene Lösung, die Symbole (x) markieren die ``numerisch exakte'' Lösung, die mit Hilfe der bereits vorhandenen Kosinusfunktion berechnet ist.

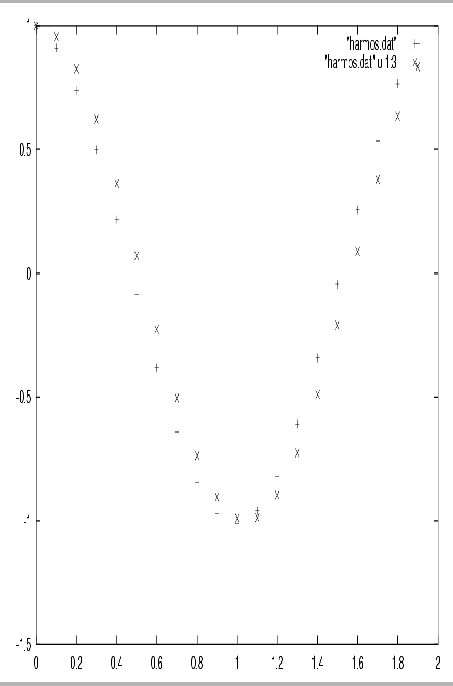Das Ergebnis ist in der Abbildung graphisch dargestellt. Dazu wurde das Programm gnuplot. (Ein weiteres Programm ist xmgr bzw. xmgrace). Nach Eingabe des Kommandos gnuplot erscheint eine Meldung des Programms und der sog. Prompt: `>'. Dann gibt man den Befehl

plot "harmos.dat","harmos.dat" u 1:3

ein. Man sollte dann die Grafik, wie in Abb. , auf dem Bildschirm erscheinen sehen.

Dieses Beispiel kann zusammen mit anderen in der ersten Übung ausprobiert werden. Ausserdem sollte ausprobiert werden, was passiert, wenn man statt des Algorithmus () den Algorithmus () benutzt.