Die erste Ableitung

Wir kehren zum Beispiel des harmonischen Oszillators in der Einleitung zurück. Dort hatten wir in Gleichung ()

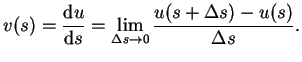$$v(s)=\frac{\mbox{\rm d}u}{\mbox{\rm d}s}=\lim_{\Delta s\to 0}\frac{u(s+\Delta s)-u(s)}{\Delta s}.$$ (4.1)

die erste Ableitung der Auslenkung $u(s)$ definiert.

Die diskrete, mittlere Geschwindigkeit kann man durch Messung des zurückgelegten Weges $u_i$ zu bestimmten Zeitpunkten $s_i$ bestimmen (wobei $i=1, ..., N$). Man erhält eine Tabelle mit $N$ Datenpunkten, aus denen die Steigung $\dot{u}(s)$ der Kurve $u(u)$ bestimmt werden kann. Mit $u_i= u(s_i)$ und $v_i=v(s_i)$ kann man die folgenden drei einfachsten Möglichkeiten definieren:

1. ,,vorwärts Ableiten'':

$$v_i^v= \frac{u_{i+1}-u_i}{s_{i+1}-s_i}$$ (4.2)

(es wird der ,,vorwärts'' nächstliegende Punkt $u(s_{i+1})$ zu Hilfe genommen)

2. ,,rückwärts Ableiten'':

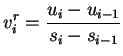$$v_i^r=\frac{u_{i}-u_{i-1}}{s_{i}-s_{i-1}}$$ (4.3)

(es wird der ,,rückwärts'' nächstliegende Punkt $u(s_{i-1})$ zu Hilfe genommen)

3. ``zentrales Ableiten'':

$$v_i^z=\frac{u_{i+1}-u_{i-1}}{s_{i+1}-s_{i-1}}$$ (4.4)

(die beiden Punkte vor und nach $u(s_i)$ werden benutzt)

Frage:
Welche dieser drei Möglichkeiten gibt den besten bzw. genauesten Wert der Ableitung?

Mit $h := s_{i+1}-s_i \forall i$ ist die Taylorentwicklung für $u(s \pm h)$:

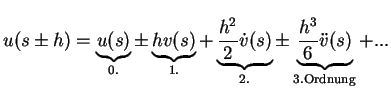$$u(s \pm h) = \underbrace{u(s)}_{0.} \pm \underbrace{h v(s)}_{1.} ... ...ot{v}(s)}_{2.} \pm \underbrace{\frac{h^3}{6}\ddot{v}(s)}_{{\rm 3. Ordnung}}+...$$ (4.5)

Damit erhält man für die obigen Ableitungsformeln ()-()

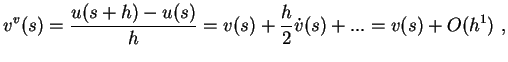$$v^v(s)= \frac{u(s+h)-u(s)}{h} = v(s) + \frac{h}{2} \dot{v}(s)+... = v(s) + O(h^1) ,$$ (4.6)

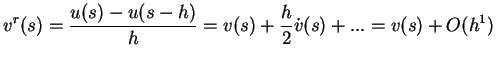$$v^r(s)= \frac{u(s)-u(s-h)}{h} = v(s) + \frac{h}{2} \dot{v}(s)+... = v(s) + O(h^1)$$ (4.7)

und

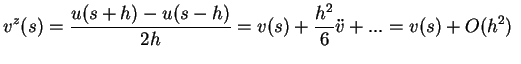$$v^z(s)=\frac{u(s+h)-u(s-h) }{2h} = v(s)+ \frac{h^2}{6} \ddot{v}+... = v(s) + O(h^2)$$ (4.8)

Der Fehler von $v^v(s)$ und $v^r(s)$ ist also von 1. Ordnung, während der Fehler von $v^z(s)$ nur von 2. Ordnung in $h$ ist, d.h. $v^z(s)$ stellt die ``bessere'' Ableitung dar.

Die numerische Ableitung kann systematisch weiter verbessert werden: Eine Formel mit Genauigkeit höherer Ordnung wäre z.B.:

$$v_i^{sz}=\frac{1}{12h}(-u_{i+2}+8u_{i+1}-8u_{i-1}+u_{i-2})$$ (4.9)

Aufgabe 1: Zeigen Sie durch Taylorentwicklung von $u(s \pm 2h)$ und $u(s \pm h)$, daß $v_i^{sz}$ aus () die Ableitung bis auf Terme der Ordnung $h^4$ richtig wiedergibt!

Aufgabe 2: Man berechne den Fehler in der numerischen Ableitung von $f(x)=\sin(x)$ an der Stelle $x=1$ im Vergleich zum exakten Wert für $h=10^{-i}$ mit $i=1,...,20$.