Die zweite Ableitung

Für höhere Ableitungen gibt es ähnliche Entwicklungen wie oben gezeigt; diese sind manchmal zur Lösung von Differentialgleichungen nötig:

$$\begin{eqnarray}a(s) & = & \dot{v}(s) = \ddot{u}(s) \nonumber \\ a_i & = & \fr... ...\frac{u_i-u_{i-1}}{h}}{h} = \frac{u_{i+1}-2u_i+u_{i-1}}{h^2} . \end{eqnarray}$$

Der Quotient in Gleichung () kann durch eine Vorwärts- mit darauffolgender Rückwärts-Ableitung berechnet werden. Die auftretenden Restterme in Gleichung () sind von Ordnung 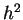$h^2$.

Eine Formel für die zweite Ableitung mit Fehler 4. Ordnung in 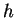$h$ ist z.B.

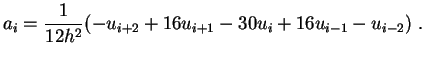$$a_i=\frac{1}{12h^2}(-u_{i+2}+16u_{i+1}-30 u_i + 16u_{i-1}-u_{i-2}) .$$ (4.10)