3 Almost invariant states

[631.2.1] Strictly stationary or invariant states [15] are an idealization. [631.2.2] In experiments stationarity is never ideal, but only approximate. [631.2.3] Expectation values are uncertain within the accuracy of the experiment. [631.2.4] Experimental accuracy depends on the response and integration times of the experimental apparatus.

[631.3.1] These experimental restrictions suggest to focus on a class of states that are stationary (invariant) only up to a given experimental accuracy $\varepsilon$ . [631.3.2] To do so, recall the definition of invariant (stationary) states. [631.3.3] A state $\mathsf{z}\in\mathfrak{A}^{*}$ is called invariant, if

$\displaystyle\left\langle\mathsf{z},T^{t}A\right\rangle=\left\langle\mathsf{z},A\right\rangle$

(15)

holds for all $A\in\mathfrak{A}$ and $t\in\mathbb{R}$ , i.e. if the expectation values $\left\langle A\right\rangle _{{\mathsf{z}}}(t)=\langle\mathsf{z},A\rangle$ of all observables $A\in\mathfrak{A}$ are constant. [631.3.4] The set of invariant states ${\mathsf{B}_{0}}\subset\mathfrak{A}^{*}$ over $\mathfrak{A}$ is convex and compact in the weak*-topology [6]. [631.3.5] The same holds for the set of all states $\mathsf{Z}\supset{\mathsf{B}_{0}}$ . [631.3.6] Invariant states are fixed points of the adjoint time evolution $T^{{*t}}$ as seen from eq. (8). [631.3.7] Because invariant states are fixed points of $T^{{*t}}$ , they are of limited benefit for a proper mathematical formulation of the problems discussed above. [631.3.8] Once an orbit in state space reaches an invariant state, it remains forever in that state and cannot leave it.

[631.4.1] Almost invariant states are based on states whose expectation values are of bounded mean oscillation (BMO). [631.4.2] A state $\mathsf{z}\in\mathsf{Z}$ is called a BMO-state if all maps $\left\langle A\right\rangle _{{\mathsf{z}}}\colon\mathbb{R}\to\mathbb{R}$ have bounded mean oscillation for all $A\in\mathfrak{A}$ . [631.4.3] The Banach space ${\rm BMO}(\mathbb{R})$ of functions with bounded mean oscillation on $\mathbb{R}$ is defined as the linear space

$\displaystyle{\rm BMO}(\mathbb{R})=\{ f\in L^{1}_{{\rm loc}}(\mathbb{R}),\left\| f\right\| _{{{\rm BMO}}}<\infty\}$

(16)

where $L^{1}_{{\rm loc}}(\mathbb{R})$ is the space of locally integrable functions $f\colon\mathbb{R}\to\mathbb{R}$ . [631.4.4] The BMO-norm is defined as

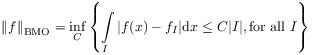$\displaystyle\left\| f\right\| _{{{\rm BMO}}}=\inf _{C}\left\{\int\limits _{I}|f(x)-f_{I}|\mathrm{d}x\leq C|I|,\text{for all~}I\right\}$

(17)

where $I\subset\mathbb{R}$ denotes intervals of length $|I|$ and

$\displaystyle f_{I}=\frac{1}{|I|}\int\limits _{I}f(x)\mathrm{d}x$

(18)

denotes the average of $f$ over the interval $I$ . [631.4.5] The set of all BMO-states

$\displaystyle\mathsf{B}=\left\{\mathsf{z}\in\mathsf{Z}:\left\|\left\langle A\right\rangle _{{\mathsf{z}}}\right\| _{{{\rm BMO}}}<\infty\text{~~for all~}A\in\mathfrak{A}\right\}$

(19)

is convex by linearity. [631.4.6] As a subset $\mathsf{B}\subset\mathsf{Z}$ of a weak* compact set it is itself weak* compact. [631.4.7] Hence a decomposition theory into extremal BMO-states exists by virtue of the Krein-Milman theorem. [631.4.8] The set of invariant states is identified through

$\displaystyle{\mathsf{B}_{0}}=\left\{\mathsf{z}\in\mathsf{B}:\left\|\left\langle A\right\rangle _{{\mathsf{z}}}\right\| _{{{\rm BMO}}}=0\text{~~for all~}A\in\mathfrak{A}\right\}$

(20)

as a subset ${\mathsf{B}_{0}}\subset\mathsf{B}$ .

[page 632, §1] [632.1.1] A BMO-state will be called $\varepsilon$ -almost invariant or almost invariant with accuracy $\varepsilon$ if the expectation of all observables are stationary to within experimental accuracy $\varepsilon$ . [632.1.2] More precisely, the set $\mathsf{B}_{\varepsilon}$ of all $\varepsilon$ -almost invariant states is defined as

$\displaystyle\mathsf{B}_{\varepsilon}=\left\{\mathsf{z}\in\mathsf{B}:\left\|\left\langle A\right\rangle _{{\mathsf{z}}}\right\| _{{{\rm BMO}}}<\varepsilon\text{~~for all~}A\in\mathfrak{A}\right\}$

(21)

as a family of subsets of $\mathsf{B}$ . [632.1.3] For small $\varepsilon\to 0$ these states are almost invariant. [632.1.4] The accuracy $\varepsilon$ measures temporal fluctuations away from the time average.

[632.2.1] The following inclusions of classes of states used in the following are summarized for orientation and convenience

$\displaystyle\mathsf{K}_{\beta}\subset{\mathsf{B}_{0}}\subset\mathsf{B}_{\varepsilon}\subset\mathsf{B}_{\infty}=\mathsf{B}\subset\mathsf{Z}\subset\mathfrak{A}^{*}$

(22)

where $0<\varepsilon<\infty$ and the set of KMS-states $\mathsf{K}_{\beta}$ at inverse temperature $\beta>0$ are defined as states $\mathsf{z}\in\mathsf{Z}$ such that the KMS-condition[16]

$\displaystyle\left\langle\mathsf{z},T^{{t/\tau}}(A)B\right\rangle=\left\langle\mathsf{z},BT^{{t/\tau+\mathrm{i}\epsilon\beta}}(A)\right\rangle$

(23)

holds for all $t/\tau\in\mathbb{R}$ and $A,B\in\mathfrak{A}$ . [632.2.2] The KMS-states are invariant states for all $\beta\geq 0$ , but KMS-states for different $\beta$ are disjoint [16]. [632.2.3] For $\beta=0$ the KMS-states are trace states, i.e. $\langle\mathsf{z},AB\rangle=\langle\mathsf{z},BA\rangle$ holds for all $A,B\in\mathfrak{A}$ . [632.2.4] Because KMS-states are Gibbs states they are usually interpreted as equilibrium states with extremal states corresponding to pure thermodynamic phases [16].

Author:	R. Hilfer
originally published in:	Mathematics, Vol. 3, pages 626-643 (2015)
originally submitted:	March 24th 2015