Sie sind hier: ICP » R. Hilfer » Publikationen

5 Invariant Measures on BMO-states

[page 633, §1]   
[633.1.1] The set of BMO-states \mathsf{B} is weak*-compact. [633.1.2] Its open subsets are the elements of the weak*-topology restricted to \mathsf{B}. [633.1.3] They generate the \sigma-algebra \mathcal{B} of Borel sets on \mathsf{B}. [633.1.4] Let \mathsf{z}\in{\mathsf{B}_{0}}\subset\mathsf{B} denote an invariant state so that eq. (15) holds for all t\in\mathbb{R},A\in\mathfrak{A}. [633.1.5] An invariant probability measure on \mathsf{B} corresponding to the invariant \mathsf{z} can be constructed with the help of a resolution of the identity on \mathcal{B}.

[633.2.1] Let (\mathfrak{H}_{\mathsf{z}},\pi _{\mathsf{z}},\Omega _{\mathsf{z}},U_{\mathsf{z}}^{t}) denote the cyclic representation canonically associated with an invariant state \mathsf{z}\in\mathsf{B} and the time evolution T^{t} on \mathfrak{A}. [633.2.2] It is uniquely determined by the two requirements

\displaystyle U_{\mathsf{z}}^{t}\;\pi _{\mathsf{z}}(A)\; U_{\mathsf{z}}^{{-t}}=\pi _{\mathsf{z}}\left(T^{t}A\right) (26)

for A\in\mathfrak{A}, t\in\mathbb{R} and

\displaystyle U_{\mathsf{z}}^{t}\;\Omega _{\mathsf{z}}=\Omega _{\mathsf{z}} (27)

for t\in\mathbb{R}. [633.2.3] Let (~,~) denotes the scalar product in \mathfrak{H}_{\mathsf{z}}.

[633.3.1] A resolution of the identity[13, p.301] on the Borel \sigma-algebra \mathcal{B} is a mapping

P:\mathcal{B}\to\mathfrak{B}(\mathfrak{H}_{\mathsf{z}}) (28)

with the properties

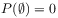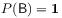
  1. P(\emptyset)=0, P(\mathsf{B})=\mathbf{1}

  2. Each 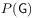P(\mathsf{G}) is a self-adjoint projector.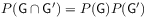

  3. P(\mathsf{G}\cap\mathsf{G}^{{\prime}})=P(\mathsf{G})P(\mathsf{G}^{{\prime}})

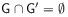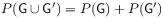
  4. If \mathsf{G}\cap\mathsf{G}^{{\prime}}=\emptyset then P(\mathsf{G}\cup\mathsf{G}^{{\prime}})=P(\mathsf{G})+P(\mathsf{G}^{{\prime}})

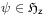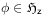  5. For every \psi\in\mathfrak{H}_{\mathsf{z}} and \phi\in\mathfrak{H}_{\mathsf{z}} the set function 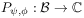P_{{\psi,\phi}}:\mathcal{B}\to\mathbb{C} defined by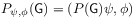

    \displaystyle P_{{\psi,\phi}}(\mathsf{G})=\left(P(\mathsf{G})\psi,\phi\right) (29)

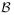    is a complex regular Borel measure on \mathcal{B}.

[633.3.2] Because the projectors are self-adjoint the set function P_{{\psi,\psi}} is a positive measure for every \psi\in\mathfrak{H}_{\mathsf{z}}. [633.3.3] For \psi=\phi=\Omega _{\mathsf{z}} the resulting measure

\displaystyle P_{{\Omega _{\mathsf{z}},\Omega _{\mathsf{z}}}}=\left(P(\mathsf{G})\Omega _{\mathsf{z}},\Omega _{\mathsf{z}}\right)=:P_{\mathsf{z}} (30)

is an invariant probability measure on the measurable space (\mathsf{B},\mathcal{B}) associated with the invariant BMO-state \mathsf{z}\in\mathsf{B}. [633.3.4] The triple (\mathsf{B},\mathcal{B},P_{\mathsf{z}}) is a probability space. [633.3.5] The probability measure P_{\mathsf{z}} is invariant under the adjoint time evolution T^{{*t}} on \mathsf{B}.