7 Results

[635.1.1] The time evolution of almost invariant states can be defined by the addition of random recurrence times. [635.1.2] Let $p_{N}(k)$ be the probability density of the sum

$W_{N}=w_{1}+\dots+w_{N}$

(40)

of $N\geq 1$ independent and identically-distributed random recurrence times $w_{i}\geq 1$ . [635.1.3] Let $p(k)$ from Equation (39) be the common probability density of all $w_{i}$ . [635.1.4] Then, with $N\geq 2$ and $p_{1}(k)=p(k)$ ,

$\displaystyle p_{N}(k)=(p_{{N-1}}*p)(k)=\sum _{{m=0}}^{k}p_{{N-1}}(m)p(k-m)$

(41)

is an $N$ -fold convolution of the discrete recurrence time density in Equation (39). [635.1.5] The family of distributions $p_{N}(k)$ obeys

$\displaystyle p_{N}(\infty)+\sum _{{k=1}}^{\infty}p_{N}(k)=1$

(42)

for all $N\geq 1$ , and the discrete analogue of Equation (5)

$\displaystyle p_{{N+M}}(k)=(p_{N}*p_{M})(k)$

(43)

holds for all $N,M\geq 1$ . [635.1.6] Because the individual states in $\mathsf{G}$ are indistinguishable within the given accuracy $\eta$ , but may evolve very differently in time, it is natural to define the duration of time needed for the first recurrence (a single time step) as an average

$\displaystyle\mathscr{S}^{{-1}}=\sum _{{k=1}}^{\infty}p(k)\;\mathscr{T}^{{-k}}$

(44)

over recurrence times. [635.1.7] If a macroscopic time evolution with a rescaled time exists, then one has to rescale the sums $W_{N}$ and the iterations

$\displaystyle\mathscr{S}^{{-N}}=\mathscr{S}^{{-(N-1)}}\mathscr{S}^{{-1}}=\sum _{{k=1}}^{\infty}p_{N}(k)\;\mathscr{T}^{{-k}}$

(45)

in the limit $N\to\infty$ with suitable norming constants $D_{N}\geq 0$ .

Theorem 3.

[635.1.8] Let $p_{N}(k)$ be the probability density of $W_{N}$ specified above in (41). [635.1.9] If the distributions of $W_{N}/D_{N}$ converge to a limit as $N\to\infty$ for suitable norming constants $D_{N}\geq 0$ , then there exist constants $D\geq 0$ and $0<\alpha\leq 1$ , such that

$\lim _{{N\to\infty}}\sup _{k}\left|D_{N}p_{N}(k)-\frac{\tau}{D^{{1/\alpha}}}h_{\alpha}\left(\frac{k\tau}{D_{N}D^{{1/\alpha}}}\right)\right|=0$

(46)

[page 636, §0] where:

$\alpha=\sup\{ 0<\beta<1:\sum _{{k=1}}^{\infty}k^{\beta}p(k)<\infty\}$

(47)

if $\sum _{{k=1}}^{\infty}kp(k)$ diverges, while

$\alpha=1$

(48)

if $\sum _{{k=1}}^{\infty}kp(k)$ converges. [636.0.1] For $\alpha=1$ , the function $h_{\alpha}(x)$ is $h_{1}(x)=\delta(x-1)$ . [636.0.2] For $0<\alpha<1$ , the function $h_{\alpha}(x)=0$ for $x\leq 0$ and

$h_{\alpha}(x)=\frac{1}{x}\sum _{{j=0}}^{\infty}\frac{(-1)^{j}x^{{-\alpha j}}}{j!\;\Gamma(-\alpha j)}$

(49)

for $x>0$ .

Proof.

[636.1.1] The existence of a limiting distribution for $W_{N}/D_{N}>0$ is known to be equivalent to the stability of the limit [18]. [636.1.2] If the limit distribution is nondegenerate, this implies that the rescaling constants $D_{N}$ have the form

$D_{N}=\left(N\Lambda(N)\right)^{{1/\alpha}}$

(50)

where $\Lambda(N)$ is a slowly varying function [19], defined by the requirement that

$\lim _{{x\to\infty}}\frac{\Lambda(bx)}{\Lambda(x)}=1$

(51)

holds for all $b>0$ . [636.1.3] That the number $\alpha$ obeys Equation (47) is proven in [18] (p. 179). [636.1.4] It is bounded as $0<\alpha\leq 1$ , because the rescaled random variables $W_{N}/D_{N}>0$ are positive.

[636.2.1] To prove Equation (46), note that the characteristic function of $W_{N}$ is the $N$ -th power

$\displaystyle\langle\mathrm{e}^{{\mathrm{i}\xi W_{N}}}\rangle=\left[p(\xi)\right]^{N}=\sum _{k}\mathrm{e}^{{\mathrm{i}\xi y}}p_{N}(k)$

(52)

because the characteristic functions $p(\xi)=\langle\mathrm{e}^{{\mathrm{i}\xi w_{j}}}\rangle$ of $w_{j}$ are identical for all $j=1,...,N$ . [636.2.2] Inverse Fourier transformation gives:

$\displaystyle p_{N}(k)=\frac{1}{2\pi}\int\limits _{{-\pi}}^{{\pi}}\mathrm{e}^{{-\mathrm{i}\xi k}}\left[p(\xi)\right]^{N}\mathrm{d}\xi=\frac{\tau}{2\pi D_{N}D^{{1/\alpha}}}\int\limits _{{-\pi D_{N}D^{{1/\alpha}}}}^{{\pi D_{N}D^{{1/\alpha}}}}\mathrm{e}^{{-\mathrm{i}\xi x}}\left[p\left(\frac{\xi\tau}{D_{N}D^{{1/\alpha}}}\right)\right]^{N}\mathrm{d}\xi$

(53)

where:

$\displaystyle x=x_{{kN}}=\frac{k\tau}{D_{N}D^{{1/\alpha}}}$

(54)

and $\xi$ was substituted with $(\xi\tau)/(D_{N}D^{{1/\alpha}})$ . [636.2.3] Let $h_{\alpha}(\xi)$ denote the characteristic function of $h_{\alpha}(x)$ , so that

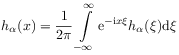$\displaystyle h_{\alpha}(x)=\frac{1}{2\pi}\int\limits _{{-\infty}}^{{\infty}}\mathrm{e}^{{-\mathrm{i}x\xi}}h_{\alpha}(\xi)\mathrm{d}\xi$

(55)

holds.

[page 637, §1] [637.1.1] Following [20], the difference $\Delta _{N}(k)$ in (46) can be decomposed and bounded from above as

$\displaystyle\Delta _{N}(k)$	$\displaystyle=\left\|D_{N}p_{N}(k)-\frac{\tau}{D^{{1/\alpha}}}h_{\alpha}\left(\frac{k\tau}{D_{N}D^{{1/\alpha}}}\right)\right\|=\left\|D_{N}p_{N}(k)-\frac{\tau}{D^{{1/\alpha}}}h_{\alpha}\left(x\right)\right\|$
	$\displaystyle=\frac{\tau}{2\pi D^{{1/\alpha}}}\left\|\int\limits _{{-\pi D_{N}D^{{1/\alpha}}}}^{{\pi D_{N}D^{{1/\alpha}}}}\mathrm{e}^{{-\mathrm{i}\xi x}}\left[p\left(\frac{\xi\tau}{D_{N}D^{{1/\alpha}}}\right)\right]^{N}\mathrm{d}\xi-\int\limits _{{-\infty}}^{{\infty}}\mathrm{e}^{{-\mathrm{i}\xi x}}\ h_{\alpha}(\xi)\mathrm{d}\xi\right\|$
	$\displaystyle=\frac{\tau}{2\pi D^{{1/\alpha}}}\left\|\;\int\limits _{{\|\xi\|<B}}\mathrm{e}^{{-\mathrm{i}\xi x}}\left[p\left(\frac{\xi\tau}{D_{N}D^{{1/\alpha}}}\right)^{N}-h_{\alpha}(\xi)\right]\mathrm{d}\xi+\int\limits _{{B\leq\|\xi\|<\eta D_{N}D^{{1/\alpha}}}}\mathrm{e}^{{-\mathrm{i}\xi x}}\left[p\left(\frac{\xi\tau}{D_{N}D^{{1/\alpha}}}\right)^{N}-h_{\alpha}(\xi)\right]\mathrm{d}\xi\right.$
	$\displaystyle\qquad\left.+\int\limits _{{\eta\leq\frac{\|\xi\|}{D_{N}D^{{1/\alpha}}}<\pi}}\mathrm{e}^{{-\mathrm{i}\xi x}}\left[p\left(\frac{\xi\tau}{D_{N}D^{{1/\alpha}}}\right)^{N}-h_{\alpha}(\xi)\right]\mathrm{d}\xi-\int\limits _{{\|\xi\|\geq\pi D_{N}D^{{1/\alpha}}}}\mathrm{e}^{{-\mathrm{i}\xi x}}\ h_{\alpha}(\xi)\mathrm{d}\xi\right\|$
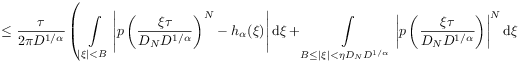	$\displaystyle\leq\frac{\tau}{2\pi D^{{1/\alpha}}}\left(\int\limits _{{\|\xi\|<B}}\left\|p\left(\frac{\xi\tau}{D_{N}D^{{1/\alpha}}}\right)^{N}-h_{\alpha}(\xi)\right\|\mathrm{d}\xi+\int\limits _{{B\leq\|\xi\|<\eta D_{N}D^{{1/\alpha}}}}\left\|p\left(\frac{\xi\tau}{D_{N}D^{{1/\alpha}}}\right)\right\|^{N}\mathrm{d}\xi\right.$
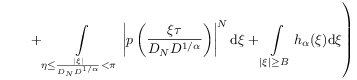	$\displaystyle\qquad\left.+\int\limits _{{\eta\leq\frac{\|\xi\|}{D_{N}D^{{1/\alpha}}}<\pi}}\left\|p\left(\frac{\xi\tau}{D_{N}D^{{1/\alpha}}}\right)\right\|^{N}\mathrm{d}\xi+\int\limits _{{\|\xi\|\geq B}}h_{\alpha}(\xi)\mathrm{d}\xi\right)$	(56)

with constants $B,\eta$ to be specified below. [637.1.2] The terms involving $h_{\alpha}(\xi)$ from the second and third integral have been absorbed in the fourth integral. [637.1.3] The four integrals are now discussed further individually.

[637.2.1] The first integral converges uniformly to zero for $N\to\infty$ , because $p(k)$ belongs to the domain of attraction of a stable law with index $\alpha$ , as already noted above.

[637.3.1] To estimate the second integral, note that the characteristic function $p(\xi)$ belongs to the domain of attraction for index $\alpha$ if and only if it behaves for $|\xi|\to 0$ as [20]

$\displaystyle|p(\xi)|=\exp\left\{-c|\xi|^{\alpha}\Lambda\left(\frac{1}{|\xi|}\right)\right\}$

(57)

where $c>0$ and $\Lambda(x)$ is a slowly varying function at infinity obeying

$\displaystyle\lim _{{N\to\infty}}\frac{N\Lambda(D_{N})}{D_{N}^{\alpha}}=1$

(58)

[637.3.2] By the representation theorem for slowly varying functions ([21] p. 12), there exist functions $d(y)$ and $\varepsilon(y)$ , such that the function $\Lambda(y)$ can be represented as

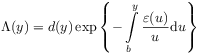$\displaystyle\Lambda(y)=d(y)\exp\left\{-\int\limits _{b}^{y}\frac{\varepsilon(u)}{u}\mathrm{d}u\right\}$

(59)

[page 638, §0] for some $b>0$ where $d(y)$ is measurable and $d(y)\to d\in(0,\infty)$ , as well as $\varepsilon(u)\to 0$ hold for $y\to\infty$ . [638.0.1] As a consequence

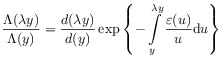$\displaystyle\frac{\Lambda(\lambda y)}{\Lambda(y)}=\frac{d(\lambda y)}{d(y)}\exp\left\{-\int\limits _{{y}}^{{\lambda y}}\frac{\varepsilon(u)}{u}\mathrm{d}u\right\}$

(60)

so that with $\lambda=|\xi|^{{-1}}$ and $y=D_{N}$

$\displaystyle\frac{\Lambda(D_{N}/|\xi|)}{\Lambda(D_{N})}=|\xi|^{{o(1)}}(1+o(1))$

(61)

is obtained for $N\to\infty$ . [638.0.2] Therefore, there exists for any $\gamma<\alpha$ a positive number $c(\gamma)$ independent of $N$ , such that

$\displaystyle|p_{N}(\xi)|=\left|p\left(\frac{\xi}{D_{N}}\right)\right|^{N}=\left|\exp\left\{-\frac{cN}{D_{N}^{\alpha}}\frac{\Lambda(D_{N})}{\Lambda(D_{N})}\Lambda\left(\frac{D_{N}}{\xi}\right)|\xi|^{\alpha}\right\}\right|\leq\exp\left\{-c(\gamma)|\xi|^{\gamma}\right\}$

(62)

for sufficiently large $N$ . [638.0.3] If $N$ is sufficiently large, it is then possible to choose an $\eta>0$ (and find $\widetilde{c}(\gamma)$ ), such that

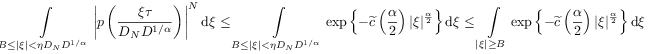$\int\limits _{{B\leq|\xi|<\eta D_{N}D^{{1/\alpha}}}}\left|p\left(\frac{\xi\tau}{D_{N}D^{{1/\alpha}}}\right)\right|^{N}\mathrm{d}\xi\leq\int\limits _{{B\leq|\xi|<\eta D_{N}D^{{1/\alpha}}}}\exp\left\{-\widetilde{c}\left(\frac{\alpha}{2}\right)|\xi|^{{\frac{\alpha}{2}}}\right\}\mathrm{d}\xi\leq\int\limits _{{|\xi|\geq B}}\exp\left\{-\widetilde{c}\left(\frac{\alpha}{2}\right)|\xi|^{{\frac{\alpha}{2}}}\right\}\mathrm{d}\xi$

(63)

and this converges to zero for $B\to\infty$ .

[638.1.1] The third integral is estimated by noting that $|p(\xi)|<1$ for $0<|\xi|<2\pi/\tau$ . [638.1.2] Hence, there is a positive constant $c>0$ , such that

$\displaystyle|p(\xi)|\leq\mathrm{e}^{{-c}}$

(64)

for $\eta\leq|\xi|\leq\pi$ . [638.1.3] Consequently, with Equation (50),

$\displaystyle\int\limits _{{\eta\leq\frac{|\xi|}{D_{N}D^{{1/\alpha}}}<\pi}}\left|p\left(\frac{\xi\tau}{D_{N}D^{{1/\alpha}}}\right)\right|^{N}\mathrm{d}\xi\leq 2\pi\mathrm{e}^{{-cN}}\left[N\Lambda(N)D\right]^{{1/\alpha}}$

(65)

converges to zero as $N\to\infty$ .

[638.2.1] Finally, the fourth integral converges to zero, because the characteristic function $h_{\alpha}(\xi)$ is integrable on $\mathbb{R}$ . [638.2.2] In summary, all four terms in Equation (56) vanish for $N\to\infty$ , and Equation (46) holds. ∎

[638.3.1] Equation (46) implies

$p_{N}(k)\approx\frac{\tau}{D_{N}D^{{1/\alpha}}}\; h_{\alpha}\left(\frac{k\tau}{D_{N}D^{{1/\alpha}}}\right)$

(66)

for sufficiently large $N$ and all $\tau$ . [638.3.2] Inserting this into Equation (45) gives

$\mathscr{S}^{{-N}}=\sum _{{k=1}}^{\infty}p_{N}(k)\;\mathscr{T}^{{-k}}\approx\sum _{{k=1}}^{\infty}\frac{\tau}{D_{N}D^{{1/\alpha}}}\; h_{\alpha}\left(\frac{k\tau}{D_{N}D^{{1/\alpha}}}\right)\;\mathscr{T}^{{-k}}=\sum _{{k=1}}^{\infty}h_{\alpha}\left(\frac{k\tau}{D_{N}D^{{1/\alpha}}}\right)\;\mathscr{T}^{{-k}}\;\frac{[k-(k-1)]\tau}{D_{N}D^{{1/\alpha}}}$

(67)

[page 639, §0] [639.0.1] For $\alpha=1$ , the average return time $\tau\sum _{k}kp(k)<\infty$ is proportional to the discretization $\tau$ . [639.0.2] In the case $0<\alpha<1$ , the average time $\tau\sum _{k}kp(k)=\infty$ for return into the set $\mathsf{G}$ in a single step diverges. [639.0.3] This suggests an infinite rescaling of time as $\tau\to\infty$ for $0<\alpha<1$ . [639.0.4] This rescaling of time combined with $N\to\infty$ was called the ultra-long-time limit in [22]. [639.0.5] In the ultra-long-time limit $N\to\infty,\tau\to\infty$ with:

$\displaystyle\lim _{{{\tau\to\infty}\atop{N\to\infty}}}\frac{D_{N}D^{{1/\alpha}}}{\tau}=\lim _{{{\tau\to\infty}\atop{N\to\infty}}}\frac{[N\Lambda(N)D]^{{1/\alpha}}}{\tau}=a$

(68)

one finds from Equation (67) the result

$\displaystyle\lim _{{{\tau\to\infty,N\to\infty}\atop{[N\Lambda(N)D]^{{1/\alpha}}/\tau=a}}}\mathscr{S}^{{-N}}\approx\sum _{{k=1}}^{\infty}h_{\alpha}\left(\frac{k}{a}\right)\;\mathscr{T}^{{-ka}}\;\frac{[k-(k-1)]}{a}\approx\int\limits _{0}^{\infty}h_{\alpha}\left(x\right)\;\mathscr{T}^{{-xa}}\;\mathrm{d}x$

(69)

for sufficiently large $N$ and $\tau$ . [639.0.6] The limit gives rise to a family of one-parameter semigroups $\mathscr{T}^{a}_{{\alpha}}$ (with family index $\alpha$ and parameter $a$ ) of ultra-long-time evolution operators

$\displaystyle\lim _{{{\tau\to\infty,N\to\infty}\atop{[N\Lambda(N)D]^{{1/\alpha}}/\tau=a}}}\mathscr{S}^{{-N}}=\mathscr{T}^{{-a}}_{{\alpha}}=\int\limits _{0}^{\infty}h_{\alpha}\left(x\right)\;\mathscr{T}^{{-xa}}\;\mathrm{d}x$

(70)

which are convolutions instead of translations. [639.0.7] Note that $a\geq 0$ because $D_{N}\geq 0$ and $D\geq 0$ . [639.0.8] The rescaled age evolutions $\mathscr{T}^{{-a}}_{{\alpha}}$ are called fractional time evolutions, because their infinitesimal generators are fractional time derivatives [22, 23].

[639.1.1] The result shows that a proper mathematical formulation of local stationarity requires a generalization of the left-hand side in Equation (1), because Equation (1) assumes implicitly a translation along the orbit. [639.1.2] In general, the integration of infinitesimal system changes leads to convolutions instead of just translations along the orbit [22, 23]. [639.1.3] Of course, translations are a special case of convolutions, to which they reduce in the case when the parameter $\alpha$ approaches unity. [639.1.4] For $\alpha\to 1^{-}$ , one finds

$h_{1}(x)=\lim _{{\alpha\to 1^{-}}}h_{\alpha}(x)=\delta(x-1)$

(71)

and therefore

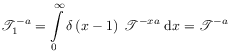$\mathscr{T}^{{-a}}_{{1}}=\int\limits _{0}^{\infty}\delta\left(x-1\right)\;\mathscr{T}^{{-xa}}\;\mathrm{d}x=\mathscr{T}^{{-a}}$

(72)

is a right translation. [639.1.5] Here, $a\geq 0$ is an age or duration. [639.1.6] This shows that also the special case of induced right translations does not give a group, but only a semigroup.

Author:	R. Hilfer
originally published in:	Mathematics, Vol. 3, pages 626-643 (2015)
originally submitted:	March 24th 2015

$\displaystyle\Delta _{N}(k)$	$\displaystyle=\left\|D_{N}p_{N}(k)-\frac{\tau}{D^{{1/\alpha}}}h_{\alpha}\left(\frac{k\tau}{D_{N}D^{{1/\alpha}}}\right)\right\|=\left\|D_{N}p_{N}(k)-\frac{\tau}{D^{{1/\alpha}}}h_{\alpha}\left(x\right)\right\|$
	$\displaystyle=\frac{\tau}{2\pi D^{{1/\alpha}}}\left\|\int\limits _{{-\pi D_{N}D^{{1/\alpha}}}}^{{\pi D_{N}D^{{1/\alpha}}}}\mathrm{e}^{{-\mathrm{i}\xi x}}\left[p\left(\frac{\xi\tau}{D_{N}D^{{1/\alpha}}}\right)\right]^{N}\mathrm{d}\xi-\int\limits _{{-\infty}}^{{\infty}}\mathrm{e}^{{-\mathrm{i}\xi x}}\ h_{\alpha}(\xi)\mathrm{d}\xi\right\|$
	$\displaystyle=\frac{\tau}{2\pi D^{{1/\alpha}}}\left\|\;\int\limits _{{\|\xi\|<B}}\mathrm{e}^{{-\mathrm{i}\xi x}}\left[p\left(\frac{\xi\tau}{D_{N}D^{{1/\alpha}}}\right)^{N}-h_{\alpha}(\xi)\right]\mathrm{d}\xi+\int\limits _{{B\leq\|\xi\|<\eta D_{N}D^{{1/\alpha}}}}\mathrm{e}^{{-\mathrm{i}\xi x}}\left[p\left(\frac{\xi\tau}{D_{N}D^{{1/\alpha}}}\right)^{N}-h_{\alpha}(\xi)\right]\mathrm{d}\xi\right.$
	$\displaystyle\qquad\left.+\int\limits _{{\eta\leq\frac{\|\xi\|}{D_{N}D^{{1/\alpha}}}<\pi}}\mathrm{e}^{{-\mathrm{i}\xi x}}\left[p\left(\frac{\xi\tau}{D_{N}D^{{1/\alpha}}}\right)^{N}-h_{\alpha}(\xi)\right]\mathrm{d}\xi-\int\limits _{{\|\xi\|\geq\pi D_{N}D^{{1/\alpha}}}}\mathrm{e}^{{-\mathrm{i}\xi x}}\ h_{\alpha}(\xi)\mathrm{d}\xi\right\|$
	$\displaystyle\leq\frac{\tau}{2\pi D^{{1/\alpha}}}\left(\int\limits _{{\|\xi\|<B}}\left\|p\left(\frac{\xi\tau}{D_{N}D^{{1/\alpha}}}\right)^{N}-h_{\alpha}(\xi)\right\|\mathrm{d}\xi+\int\limits _{{B\leq\|\xi\|<\eta D_{N}D^{{1/\alpha}}}}\left\|p\left(\frac{\xi\tau}{D_{N}D^{{1/\alpha}}}\right)\right\|^{N}\mathrm{d}\xi\right.$
	$\displaystyle\qquad\left.+\int\limits _{{\eta\leq\frac{\|\xi\|}{D_{N}D^{{1/\alpha}}}<\pi}}\left\|p\left(\frac{\xi\tau}{D_{N}D^{{1/\alpha}}}\right)\right\|^{N}\mathrm{d}\xi+\int\limits _{{\|\xi\|\geq B}}h_{\alpha}(\xi)\mathrm{d}\xi\right)$	(56)