Sie sind hier: ICP » R. Hilfer » Publikationen

6 Almost Invariance and Recurrence

[page 634, §1]   
[634.1.1] To discuss the question how invariant states can evolve in time (Problem 2) consider two invariant states \mathsf{u},\mathsf{v}\in{\mathsf{B}_{0}} and the straight line segment

\displaystyle\mathsf{S}=\left\{\mathsf{z}=\lambda\mathsf{u}+(1-\lambda)\mathsf{v},0\leq\lambda\leq 1,\mathsf{u}\in{\mathsf{B}_{0}},\mathsf{v}\in{\mathsf{B}_{0}}\right\} (31)

connecting \mathsf{u} and \mathsf{v}. [634.1.2] Of course \mathsf{S}\subset{\mathsf{B}_{0}}. [634.1.3] In practical applications \mathsf{S} might be a more or less general subset of {\mathsf{B}_{0}}, e.g., a KMS-state in \bigcup _{\beta}\mathsf{K}_{\beta}. [634.1.4] Straight line segments of invariant states are expected to be physically important for phase transformations at thermodynamic coexistence. [634.1.5] Define a weak*-neighbourhood

\displaystyle\mathsf{G}=\mathsf{B}_{{\varepsilon}}\cap\left(\bigcup _{{\mathsf{z}\in\mathsf{S}}}\mathsf{N}(\mathsf{z},\{ A\} _{1}^{m};\eta)\right) (32)

of \varepsilon-almost invariant \eta-indistinguishable states near \mathsf{S}. [634.1.6] Depending on the invariant states \mathsf{S} and macroscopic algebra \mathfrak{M} of interest a similar weak*-neighbourhood \mathsf{G}=\mathsf{G}(\mathsf{S},\mathfrak{M},\varepsilon,\eta) can be defined for other subsets of {\mathsf{B}_{0}}.

[634.2.1] The time translations \mathscr{T}^{{-t/\tau}} with time scale \tau translate any initial state \mathsf{z}\in\mathsf{G} along its orbit according to

\displaystyle\mathscr{T}^{{-t/\tau}}\mathcal{K}_{\mathsf{z}}\left(\frac{t_{0}}{\tau}\right)=\mathcal{K}_{\mathsf{z}}\left(\frac{t_{0}-t}{\tau}\right) (33)

where t_{0} denotes the initial instant, \mathcal{K}_{\mathsf{z}}(t_{0}/\tau)=\mathsf{z} and \tau>0 the time scale. [634.2.2] Discretizing time as

t=k\tau (34)

with k\in\mathbb{Z} such that t_{0}=0 produces discretized orbits \mathcal{K}_{\mathsf{z}}(-k), k\in\mathbb{N} for all \mathsf{z}\in\mathsf{G} as iterates of \mathscr{T}^{1}. [634.2.3] For every initial state \mathsf{z}\in\mathsf{G} define

\displaystyle{w_{\mathsf{G}}}(\mathsf{z})=\min\left\{ k\geq 1:\mathscr{T}^{{-k}}\mathcal{K}_{\mathsf{z}}(0)\in\mathsf{G}\right\} (35)

as the first return time of \mathsf{z} into the set \mathsf{G}. [634.2.4] For all invariant \mathsf{z}\in{\mathsf{B}_{0}} one has {w_{\mathsf{G}}}(\mathsf{z})=1. [634.2.5] For states \mathsf{z} that never return to \mathsf{G} one sets {w_{\mathsf{G}}}(\mathsf{z})=\infty. [634.2.6] For all k\geq 1 let

\displaystyle\mathsf{G}_{k}=\left\{\mathsf{z}\in\mathsf{G}:{w_{\mathsf{G}}}(\mathsf{z})=k\right\} (36)

denote the subset of states with recurrence time 1\leq k\leq\infty with k=\infty interpreted as

\displaystyle\mathsf{G}_{\infty}=\mathsf{G}\setminus\bigcup _{{k\in\mathbb{N}}}\mathsf{G}_{k}. (37)

[634.2.7] The states \mathsf{z}\in\mathsf{S} generate a one parameter family of resolutions of the identity resulting in a one parameter family of measures on (\mathsf{B},\mathcal{B}) denoted as P_{{\lambda\mathsf{u}+(1-\lambda)\mathsf{v}}} with \lambda\in[0,1]. [634.2.8] Their mixture

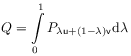\displaystyle Q=\int\limits _{0}^{1}P_{{\lambda\mathsf{u}+(1-\lambda)\mathsf{v}}}\mathrm{d}\lambda (38)

[page 635, §0]    is again an invariant measure on (\mathsf{B},\mathcal{B}). [635.0.1] The numbers

\displaystyle p(k)=\frac{Q(\mathsf{G}_{k})}{Q(\mathsf{G})} (39)

define a discrete probability density on \mathbb{N}\cup\{\infty\}. [635.0.2] It may be interpreted as a properly weighted probability of recurrence into the neighbourhood \mathsf{G} of the straight line segement \mathsf{S}\subset{\mathsf{B}_{0}}.