2.1 Historical Introduction to Fractional Derivatives

[page 17, §1]

2.1.1 Leibniz

[17.2.1] Already at the beginning of calculus one of its founding fathers, namely G.W. Leibniz, investigated fractional derivatives [73, 72]. [17.2.2] Differentiation, denoted as $\mathrm{d}^{\alpha}$ ( $\alpha\in\mathbb{N}$ ), obeys Leibniz’ product rule

$\mathrm{d}^{\alpha}(fg)=1\;\mathrm{d}^{\alpha}f\;\mathrm{d}^{0}g+\frac{\alpha}{1}\;\mathrm{d}^{{\alpha-1}}f\;\mathrm{d}^{1}g+\frac{\alpha(\alpha-1)}{1\cdot 2}\;\mathrm{d}^{{\alpha-2}}f\;\mathrm{d}^{2}g+...$

(2.1)

for integer $\alpha$ , and Leibniz was intrigued by the analogy with the binomial theorem

$\mathrm{p}^{\alpha}(f+g)=1\;\mathrm{p}^{\alpha}f\;\mathrm{p}^{0}g+\frac{\alpha}{1}\;\mathrm{p}^{{\alpha-1}}f\;\mathrm{p}^{1}g+\frac{\alpha(\alpha-1)}{1\cdot 2}\;\mathrm{p}^{{\alpha-2}}f\;\mathrm{p}^{2}g+...$

(2.2)

where he uses the notation $\mathrm{p}^{\alpha}f$ instead of $f^{\alpha}$ to emphasize the formal operational analogy.

[17.3.1] Moving from integer to noninteger powers $\alpha\in\mathbb{R}$ Leibniz suggests that "on peut exprimer par une serie infinie une grandeur comme" $\mathrm{d}^{\alpha}h$ (with $h=fg$ ). [17.3.2] As his first step he tests the idea of such a generalized differential quantity $\mathrm{d}^{\alpha}h$ against the rules of his calculus. [17.3.3] In his calculus the differential relation $\mathrm{d}h=h\mathrm{d}x$ implies $\mathrm{d}x=\mathrm{d}h/h$ and $\mathrm{d}h/\mathrm{d}x=h$ . [17.3.4] One has, therefore, also $\mathrm{d}^{2}h=h\mathrm{d}x^{2}$ and generally $\mathrm{d}^{\alpha}h=h\mathrm{d}x^{\alpha}$ . [17.3.5] Regarding $\mathrm{d}^{\alpha}h=h\mathrm{d}x^{\alpha}$ with noninteger $\alpha$ as a fractional differential relation subject to the rules of his calculus, however, leads to a paradox. [17.3.6] Explicitly, he finds (for $\alpha=1/2$ )

$\frac{\mathrm{d}^{\alpha}h}{\mathrm{d}x^{\alpha}}=\frac{\mathrm{d}^{\alpha}h}{(\mathrm{d}h/h)^{\alpha}}\neq h,$

(2.3)

where $\mathrm{d}x=\mathrm{d}h/h$ was used. [17.3.7] Many decades had to pass before Leibniz’ paradox was fully resolved.

[page 18, §1]

2.1.2 Euler

[18.1.1] Derivatives of noninteger (fractional) order motivated Euler to introduce the Gamma function [25]. [18.1.2] Euler knew that he needed to generalize (or interpolate, as he calls it) the product $1\cdot 2\cdot...\cdot n=n!$ to noninteger values of $n$ , and he proposed an integral

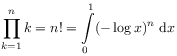$\prod _{{k=1}}^{n}k=n!=\int\limits _{0}^{1}(-\log x)^{n}\;\mathrm{d}x$

(2.4)

for this purpose. [18.1.3] In §27-29 of [25] he immediately applies this formula to partially resolve Leibniz’ paradox, and in §28 he gives the basic fractional derivative (reproduced here in modern notation with $\Gamma(n+1)=n!$ )

$\frac{\mathrm{d}^{\alpha}x^{\beta}}{\mathrm{d}x^{\alpha}}=\frac{\Gamma(\beta+1)}{\Gamma(\beta-\alpha+1)}x^{{\beta-\alpha}}$

(2.5)

valid for integer and for noninteger $\alpha,\beta$ .

2.1.3 Paradoxa and Problems

[18.2.1] Generalizing eq. (2.5) to all functions that can be expanded into a power series might seem a natural step, but this "natural" definition of fractional derivatives does not really resolve Leibniz’ paradox. [18.2.2] Leibniz had implicitly assumed the rule

$\frac{\mathrm{d}^{\alpha}\mathrm{e}^{{\lambda x}}}{\mathrm{d}x^{\alpha}}=\lambda^{\alpha}\mathrm{e}^{{\lambda x}}$

(2.6)

by demanding $\mathrm{d}^{\alpha}h=h\mathrm{d}x^{\alpha}$ for integer $\alpha$ . [18.2.3] One might therefore take eq. (2.6) instead of eq. (2.5) as an equally "natural" starting point (this was later done by Liouville in [76, p.3, eq. (1)]), and define fractional derivatives as

$\frac{\mathrm{d}^{\alpha}f}{\mathrm{d}x^{\alpha}}=\sum _{k}c_{k}\;\lambda _{k}^{\alpha}\;\mathrm{e}^{{\lambda _{k}x}}$

(2.7)

for functions representable as exponential series $f(x)\sim\sum _{k}c_{k}\exp(\lambda _{k}x)$ . [18.2.4] Regarding the integral (a Laplace integral)

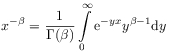$x^{{-\beta}}=\frac{1}{\Gamma(\beta)}\int\limits _{0}^{\infty}\mathrm{e}^{{-yx}}y^{{\beta-1}}\mathrm{d}y$

(2.8)

as a sum of exponentials, Liouville [76, p.7] then applied eq. (2.6) inside the integral to find

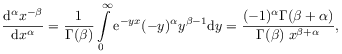$\frac{\mathrm{d}^{\alpha}x^{{-\beta}}}{\mathrm{d}x^{\alpha}}=\frac{1}{\Gamma(\beta)}\int\limits _{0}^{\infty}\mathrm{e}^{{-yx}}(-y)^{\alpha}y^{{\beta-1}}\mathrm{d}y=\frac{(-1)^{\alpha}\Gamma(\beta+\alpha)}{\Gamma(\beta)\; x^{{\beta+\alpha}}},$

(2.9)

[page 19, §0] where the last equality follows by substituting $yx=z$ in the integral. [19.0.1] If this equation is formally generalized to $-\beta$ , disregarding existence of the integral, one finds

$\frac{\mathrm{d}^{\alpha}x^{{\beta}}}{\mathrm{d}x^{\alpha}}=\frac{(-1)^{\alpha}\Gamma(-\beta+\alpha)}{\Gamma(-\beta)}\; x^{{\beta-\alpha}}$

(2.10)

a formula similar to, but different from eq. (2.5). [19.0.2] Although eq. (2.10) agrees with eq. (2.5) for integer $\alpha$ it differs for noninteger $\alpha$ . [19.0.3] More precisely, if $\alpha=1/2$ and $\beta=-1/2$ , then

$\frac{\Gamma(3/2)}{\Gamma(0)}x^{{-1}}=0\neq\frac{\mathrm{i}}{x\sqrt{\pi}}=\frac{(-1)^{{1/2}}\Gamma(1)}{\Gamma(1/2)}x^{{-1}}$

(2.11)

revealing again an inconsistency between eq. (2.5) and eq. (2.10) (resp. (2.9)).

[19.1.1] Another way to see this inconsistency is to expand the exponential function into a power series, and to apply Euler’s rule, eq. (2.5), to it. [19.1.2] One finds (with obvious notation)

$\displaystyle\left(\frac{\mathrm{d}^{\alpha}}{\mathrm{d}x^{\alpha}}\right)_{{(2.5)}}\exp(x)$	$\displaystyle=\left(\frac{\mathrm{d}^{\alpha}}{\mathrm{d}x^{\alpha}}\right)_{{(2.5)}}\sum _{{k=0}}^{\infty}\frac{x^{k}}{k!}=\sum _{{k=0}}^{\infty}\frac{x^{{k-\alpha}}}{\Gamma(k-\alpha+1)}$
	$\displaystyle\neq\left(\frac{\mathrm{d}^{\alpha}}{\mathrm{d}x^{\alpha}}\right)_{{(2.6)}}\exp(x)=\exp(x)$		(2.12)

and this shows that Euler’s rule (2.5) is inconsistent with the Leibniz/Liouville rule (2.6). [19.1.3] Similarly, Liouville found inconsistencies [75, p.95/96] when calculating the fractional derivative of $\exp(\lambda x)+\exp(-\lambda x)$ based on the definition (2.7).

[19.2.1] A resolution of Leibniz’ paradox emerges when eq. (2.5) and (2.6) are compared for $\alpha=-1$ , and interpreted as integrals. [19.2.2] Such an interpretation was already suggested by Leibniz himself [73]. [19.2.3] More specifically, one has

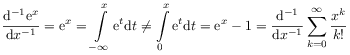$\frac{\mathrm{d}^{{-1}}\mathrm{e}^{{x}}}{\mathrm{d}x^{{-1}}}=\mathrm{e}^{{x}}=\int\limits _{{-\infty}}^{x}\mathrm{e}^{t}\mathrm{d}t\neq\int\limits _{0}^{x}\mathrm{e}^{t}\mathrm{d}t=\mathrm{e}^{x}-1=\frac{\mathrm{d}^{{-1}}}{\mathrm{d}x^{{-1}}}\sum _{{k=0}}^{\infty}\frac{x^{k}}{k!}$

(2.13)

showing that Euler’s fractional derivatives on the right hand side differs from Liouville’s and Leibniz’ idea on the left. [19.2.4] Similarly, eq. (2.5) corresponds to

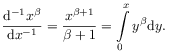$\frac{\mathrm{d}^{{-1}}x^{\beta}}{\mathrm{d}x^{{-1}}}=\frac{x^{{\beta+1}}}{\beta+1}=\int\limits _{0}^{x}y^{\beta}\mathrm{d}y.$

(2.14)

[19.2.5] On the other hand, eq. (2.9) corresponds to

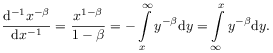$\frac{\mathrm{d}^{{-1}}x^{{-\beta}}}{\mathrm{d}x^{{-1}}}=\frac{x^{{1-\beta}}}{1-\beta}=-\int\limits _{x}^{\infty}y^{{-\beta}}\mathrm{d}y=\int\limits _{\infty}^{x}y^{{-\beta}}\mathrm{d}y.$

(2.15)

[page 20, §0] [20.0.1] This shows that Euler’s and Liouville’s definitions differ with respect to their limits of integration.

2.1.4 Liouville

[20.1.1] It has already been mentioned that Liouville defined fractional derivatives using eq. (2.7) (see [76, p.3, eq.(1)]) as

$\frac{\mathrm{d}^{\alpha}f}{\mathrm{d}x^{\alpha}}=\sum _{k}c_{k}\;\lambda _{k}^{\alpha}\;\mathrm{e}^{{\lambda _{k}x}}$

(2.7)

for functions representable as a sum of exponentials

$f(x)\sim\sum _{k}c_{k}\exp(\lambda _{k}x).$

(2.16)

[20.1.2] Liouville seems not to have recognized the necessity of limits of integration. [20.1.3] From his definition (2.7) he derives numerous integral and series representations. [20.1.4] In particular, he finds the fractional integral of order $\alpha>0$ as

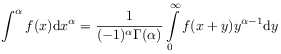$\int^{\alpha}f(x)\mathrm{d}x^{\alpha}=\frac{1}{(-1)^{\alpha}\Gamma(\alpha)}\int\limits _{0}^{\infty}f(x+y)y^{{\alpha-1}}\mathrm{d}y$

(2.17)

(see formula [A] on page 8 of [76, p.8]). [20.1.5] Liouville then gives formula [B] for fractional differentiation on page 10 of [76] as

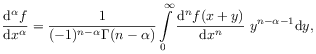$\frac{\mathrm{d}^{\alpha}f}{\mathrm{d}x^{\alpha}}=\frac{1}{(-1)^{{n-\alpha}}\Gamma(n-\alpha)}\int\limits _{0}^{\infty}\frac{\mathrm{d}^{n}f(x+y)}{\mathrm{d}x^{n}}\; y^{{n-\alpha-1}}\mathrm{d}y,$

(2.18)

where $n-1<\alpha<n$ . [20.1.6] Liouville restricts the discussion to functions represented by exponential series with $\lambda _{k}>0$ so that $f(-\infty)=0$ . [20.1.7] Liouville also expands the coefficients $\lambda _{k}^{\alpha}$ in (2.7) into binomial series

$\displaystyle\lambda _{k}^{\alpha}$	$\displaystyle=\lim _{{h\to 0}}\frac{1}{h^{\alpha}}(1-\mathrm{e}^{{-h\lambda _{k}}})^{\alpha},\qquad\lambda _{k}>0$		(2.19a)
	$\displaystyle=(-1)^{\alpha}\lim _{{h\to 0}}\frac{1}{h^{\alpha}}(1-\mathrm{e}^{{h\lambda _{k}}})^{\alpha},\qquad\lambda _{k}<0$		(2.19b)

and inserts the expansion into his defintion (2.7) to arrive at formulae that contain the representation of integer order derivatives as limits of difference quotients (see [75, p.106ff]). [20.1.8] The results may be written as

$\displaystyle\frac{\mathrm{d}^{\alpha}f}{\mathrm{d}x^{\alpha}}$	$\displaystyle=\lim _{{h\to 0}}\left\{\frac{1}{h^{\alpha}}\sum _{{m=0}}^{\infty}\left[(-1)^{m}\binom{\alpha}{m}f(x-mh)\right]\right\}$		(2.20a)
	$\displaystyle=(-1)^{\alpha}\lim _{{h\to 0}}\left\{\frac{1}{h^{\alpha}}\sum _{{m=0}}^{\infty}\left[(-1)^{m}\binom{\alpha}{m}f(x+mh)\right]\right\},$		(2.20b)

[page 21, §0] where the binomial coefficient $\binom{\alpha}{m}$ is $\Gamma(\alpha-1)\Gamma(m-1)/\Gamma(\alpha+m-1)$ . [21.0.1] Later, this idea was taken up by Grünwald [34], who defined fractional derivatives as limits of generalized difference quotients.

2.1.5 Fourier

[21.1.1] Fourier[29] suggested to define fractional derivatives by generalizing the formula for trigonometric functions,

$\frac{\mathrm{d}^{\alpha}}{\mathrm{d}x^{\alpha}}\cos(x)=\cos\left(x+\frac{\alpha\pi}{2}\right),$

(2.21)

from $\alpha\in\mathbb{N}$ to $\alpha\in\mathbb{R}$ . [21.1.2] Again, this is not unique because the generalization

$\frac{\mathrm{d}^{\alpha}}{\mathrm{d}x^{\alpha}}\cos(x)=(-1)^{\alpha}\cos\left(x-\frac{\alpha\pi}{2}\right)$

(2.22)

is also possible.

2.1.6 Grünwald

[21.2.1] Grünwald wanted to free the definition of fractional derivatives from a special form of the function. [21.2.2] He emphasized that fractional derivatives are integroderivatives, and established for the first time general fractional derivative operators. [21.2.3] His calculus is based on limits of difference quotients. [21.2.4] He studies the difference quotients [34, p.444]

$F[u,x,\alpha,h]_{f}=\sum _{{k=0}}^{n}(-1)^{k}\binom{\alpha}{k}\frac{f(x-kh)}{h^{\alpha}}$

(2.23)

with $n=(x-u)/h$ and calls

$\mathrm{D}^{{\alpha}}[f(x)]_{{x=u}}^{{x=x}}=\lim _{{h\to 0}}F[u,x,\alpha,h]_{f}$

(2.24)

the $\alpha$ -th differential quotient taken over the straight line from $u$ to $x$ [34, p.452]. [21.2.5] The title of his work emphasizes the need to introduce limits of integration into the concept of differentiation. [21.2.6] His ideas were soon elaborated upon by Letnikov (see [99])and applied to differential equations by Most [89].

2.1.7 Riemann

[21.3.1] Riemann, like Grünwald, attempts to define fractional differentiation for general classes of functions. [21.3.2] Riemann defines the $n$ -th differential quotient of a function $f(x)$ as the coeffcient of $h^{n}$ in the expansion of $f(x+h)$ into integer

[page 22, §0] powers of $h$ [96, p.354]. [22.0.1] He then generalizes this definition to noninteger powers, and demands that

$f(x+h)=\sum _{{n=-\infty}}^{{n=\infty}}c_{{n+\alpha}}(\partial^{{n+\alpha}}_{x}f)(x)\; h^{{n+\alpha}}$

(2.25)

holds for $n\in\mathbb{N},\alpha\in\mathbb{R}$ . [22.0.2] The factor $c_{{n+\alpha}}$ is determined such that $\partial^{\beta}(\partial^{\gamma}f)=\partial^{{\beta+\gamma}}f$ holds, and found to be $1/\Gamma(n+\alpha+1)$ . [22.0.3] Riemann then derives the integral representation [96, p.363] for negative $\alpha$

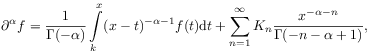$\partial^{\alpha}f=\frac{1}{\Gamma(-\alpha)}\int\limits _{k}^{x}(x-t)^{{-\alpha-1}}f(t)\mathrm{d}t+\sum _{{n=1}}^{\infty}K_{n}\frac{x^{{-\alpha-n}}}{\Gamma(-n-\alpha+1)},$

(2.26)

where $k,K_{n}$ are finite constants. [22.0.4] He then extends the result to nonnegative $\alpha$ by writing "für einen Werth von $\alpha$ aber, der $\geq 0$ ist, bezeichnet $\partial^{\alpha}f$ dasjenige, was aus $\partial^{{\alpha-m}}f$ (wo $m>\alpha$ ) durch $m$ -malige Differentiation nach $x$ hervorgeht,…" [96, p.341]. [22.0.5] The combination of Liouville’s and Grünwald’s pioneering work with this idea has become the definition of the Riemann-Liouville fractional derivatives (see Section 2.2.2.1 below).

Author:	R. Hilfer
also published in:	Anomalous Transport: Foundations and Applications, Wiley-VCH, Weinheim, page 17-73 (2008), ISBN: 978-3-527-40722-4 Copyright © 2007 R. Hilfer, Stuttgart
first published on:	June 6th, 2007