Sie sind hier: ICP » R. Hilfer » Publikationen

10 Infinitesimal Generators

[217.3.1] The operators {\rule[-2.0pt]{0.0pt}{10.0pt}_{{{G}}}\! T}_{\alpha}^{t} form a family of strongly continuous semigroups on C_{0}({G})^{*} provided that the translations T^{t} inside the integral in eq. (28) are strongly continuous [33, 48] and \int _{0}^{\infty}\| T^{s}\| h_{\alpha}(s/t)/t\mathrm{d}s<\infty. [217.3.2] In this case the infinitesimal generators for 0<\alpha\leq 1 are defined by

\mathrm{A}_{\alpha}\widetilde{\varrho}=s-lim_{{t\to 0}}\frac{{\rule[-2.0pt]{0.0pt}{10.0pt}_{{{G}}}\! T}_{\alpha}^{t}\widetilde{\varrho}-\widetilde{\varrho}}{t} (32)

for all \widetilde{\varrho}\in C_{0}({G})^{*} for which the strong limit s-lim exists. [217.3.3] In general, the infinitesimal generators are unbounded operators. [217.3.4] If \mathrm{A}=-\mathrm{d}/\mathrm{d}t denotes the infinitesimal generator of the translation T^{t} in eq. (28), then

\mathrm{A}_{\alpha}=-\left(-\mathrm{A}\right)^{\alpha}=-\left(\frac{\mathrm{d}}{\mathrm{d}t}\right)^{\alpha} (33)

are fractional time derivatives [50, 16]. [217.3.5] The action of \mathrm{A}_{\alpha} on mixed states can be represented in different ways. [217.3.6] Frequently an integral representation

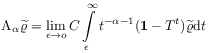\mathrm{A}_{\alpha}\widetilde{\varrho}=\lim _{{\epsilon\to o}}C\int\limits _{\epsilon}^{\infty}t^{{-\alpha-1}}(\mathbf{1}-T^{t})\widetilde{\varrho}\mathrm{d}t (34)

of Marchaud type [8, 51] is used. [217.3.7] The integral representation

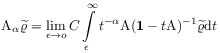\mathrm{A}_{\alpha}\widetilde{\varrho}=\lim _{{\epsilon\to o}}C\int\limits _{\epsilon}^{\infty}t^{{-\alpha}}\mathrm{A}(\mathbf{1}-t\mathrm{A})^{{-1}}\widetilde{\varrho}\mathrm{d}t (35)

[page 218, §0]    in terms of the resolvent of \mathrm{A} [12] defines the same fractional derivative operator [52]. [218.0.1] Representations of Grünwald-Letnikov type are also well known [16].

[218.1.1] In summary, fractional dynamical systems must be expected to appear generally in mathematical models of macroscopic phenomena. [218.1.2] They arise as coarse grained macroscopic time evolutions from inducing a microscopic time evolution on the subsets {G}\subset\Gamma of small measure in phase space, that are typically incurred in statistical mechanics [1, 21, 50].