| 1 |
R. Hilfer, Fractional dynamics, irreversibility and ergodicity breaking,
Chaos, Solitons & Fractals. 5, 1475, (1995).
|
| 2 |
K. Oldham and J. Spanier, The Fractional Calculus. (Academic Press, New
York, 1974).
|
| 3 |
B. Ross, The development of fractional calculus 1695-1900, Historia
Mathematica. 4, 75, (1977).
|
| 4 |
S. Samko, A. Kilbas, and O. Marichev, Fractional Integrals and
Derivatives. (Gordon and Breach, Berlin, 1993).
|
| 5 | P. Butzer and U. Westphal.
Introduction to fractional calculus.
In ed. R. Hilfer, Applications of Fractional Calculus in
Physics, p. 1, Singapore, (2000). World Scientific.
|
| 6 |
R. Hilfer.
Threefold introduction to fractional derivatives.
In eds. R. Klages, G. Radons, and I. Sokolov, Anomalous
Transport: Foundations and Applications, pp. 17–74, Weinheim, (2008).
Wiley-VCH.
|
| 7 |
S. Bochner, Harmonic Analysis and the Theory of Probability. (University
of California Press, Berkeley, 1955).
|
| 8 |
A. Balakrishnan, Fractional powers of closed operators and the semigroups
generated by them, Pacific J. Math. 10, 419, (1960).
|
| 9 |
K. Yosida, Fractional powers of infinitesimal generators and the analyticity of
the semi-groups generated by them, Proc.Japan Acad. 36,
86, (1960).
|
| 10 |
T. Kato, Note on fractional powers of linear operators, Proc.Japan Acad.
36, 94, (1960).
|
| 11 |
H. Komatsu, Fractional powers of operators, Pacific Journal of
Mathematics. 19, 285, (1966).
|
| 12 |
H. Komatsu, Fractional powers of operators II: Interpolation spaces,
Pacific Journal of Mathematics. 21, 89, (1967).
|
| 13 |
U. Westphal, Ein Kalkül für gebrochene Potenzen infinitesimaler
Erzeuger von Halbgruppen und Gruppen von Operatoren. Teil I:
Halbgruppenerzeuger, Compositio Math. 22, 67,
(1970).
|
| 14 |
U. Westphal, An approach to fractional powers of operators via fractional
differences, Proc. London Math. Soc. 29, 557, (1974).
|
| 15 |
O. Lanford and D. Robinson, Fractional powers of generators of equicontinuous
semigroups and fractional derivatives, J. Austral. Math. Soc.(A). 46, 473–504, (1989).
|
| 16 |
U. Westphal.
Fractional powers of infinitesimal generators of semigroups.
In ed. R. Hilfer, Applications of Fractional Calculus in
Physics, p. 131, Singapore, (2000). World Scientific.
|
| 17 |
R. Hilfer, Applications of Fractional Calculus in Physics. (World
Scientific Publ. Co., Singapore, 2000).
|
| 18 |
R. Hilfer, R. Metzler, A. Blumen, and J. Klafter(eds), Strange Kinetics,
Chemical Physics. 284, (2002).
|
| 19 |
R. Metzler and J. Klafter, The random walk’s guide to anomalous diffusion: a
fractional dynamics approach, Phys.Rep. 339, 1,
(2000).
|
| 20 |
R. Klages et al., Anomalous Transport. (Wiley-VCH, Weinheim, 2008).
|
| 21 | R. Hilfer, Foundations of fractional dynamics, Fractals. 3,
549, (1995).
|
| 22 |
W. Ross, Aristotelis Physica. Recognovit brevique adnotatione critica
instruxit W.D. Ross. (Oxford University Press, Oxford, 1950).
|
| 23 |
P. Mohr, B. Taylor, and D. Newell, CODATA recommended values of the
fundamental physical constants: 1998, J. Phys. Chem. Ref. Data. 37, 1187, (2008).
|
| 24 |
I. Newton, Philosophiae Naturalis Principia Mathematica. (Societas Regia
ac Joseph Streater, London, 1687).
|
| 25 |
N. Bhatia and G. Szegö, Stability Theory of Dynamical Systems.
(Springer, Berlin, 1970).
|
| 26 |
I. Cornfeld, S. Fomin, and Y. Sinai, Ergodic Theory. (Springer, Berlin,
1982).
|
| 27 | B. Mandelbrot, The Fractal Geometry of Nature. (Freeman, San Francisco,
1982).
|
| 28 |
A. Pazy, Semigroups of Linear Operators and Applications to Partial
Differential Equations. (Springer, Berlin, 1983).
|
| 29 |
E. Hille and R. Phillips, Functional Analysis and Semi-Groups. (American
Mathematical Society, Providence, 1957).
|
| 30 |
O. Bratteli and D. Robinson, Operator Algebras and Quantum Statistical
Mechanics I. (Springer, Berlin, 1979).
|
| 31 |
W. Thirring, Lehrbuch der Mathematischen Physik 3:
Quantenmechanik von Atomen und Molekülen. (Springer, Wien, 1979).
|
| 32 |
J. Neerven, The Adjoint of a Semigroup of Linear Operators. (Springer,
Berlin, 1992).
|
| 33 |
R. Phillips, On the generation of semigroups of linear operators, Pacific
J. Math. 2, 343, (1952).
|
| 34 |
J. Lebowitz, Statistical mechanics: A selective review of two central issues,
Rev.Mod.Phys. 71, S346, (1999).
|
| 35 |
R. Hilfer, Thermodynamic scaling derived via analytic continuation from the
classification of Ehrenfest, Physica Scripta. 44, 321, (1991).
|
| 36 |
R. Hilfer, Multiscaling and the classification of continuous phase transitions,
Phys. Rev. Lett. 68, 190, (1992).
|
| 37 |
R. Hilfer, Scaling theory and the classification of phase transitions,
Mod. Phys. Lett. B. 6, 773, (1992).
|
| 38 |
R. Hilfer, Classification theory for anequilibrium phase transitions,
Phys. Rev. E. 48, 2466, (1993).
|
| 39 |
R. Hilfer.
On a new class of phase transitions.
In eds. W. Beyermann, N. Huang-Liu, and D. MacLaughlin, Random
Magnetism and High-Temperature Superconductivity, p. 85, Singapore,,
(1994). World Scientific Publ. Co.
|
| 40 |
S. Kakutani, Induced measure preserving transformations, Proceedings of
the Japan Academy, Series A. 19, 635, (1943).
|
| 41 |
H. Bauer, Maß- und Integrationstheorie. (Walter de Gruyter,
Berlin, 1992).
|
| 42 |
B. Gnedenko and A. Kolmogorov, Limit Distributions for Sums of
Independent Random Variables. (Addison-Wesley, Cambridge, 1954).
|
| 43 |
H. Bergström, Limit Theorems for Convolutions. (Wiley, New York,
1963).
|
| 44 |
W. Feller, An Introduction to Probability Theory and Its Applications.
vol. II, (Wiley, New York, 1971).
|
| 45 |
I. Ibragimov and Y. Linnik, Independent and Stationary Sequences of
Random Variables. (Wolters-Nordhoff Publishing, Groningen, 1971).
|
| 46 |
E. Seneta, Regularly Varying Functions. (Springer Verlag, Berlin, 1976).
|
| 47 |
S. Bochner, Diffusion equation and stochastic processes, Proc. Natl.
Acad. Sci. USA. 35, 368, (1949).
|
| 48 |
E. Nelson, A functional calculus using singular Laplace integrals,
Trans. Amer. Math. Soc. 88, 400, (1958).
|
| 49 |
R. Hilfer.
Remarks on fractional time.
In eds. L. Castell and O. Ischebeck, Time, Quantum and
Information, p. 235, Berlin, (2003). Springer.
|
| 50 |
R. Hilfer.
Fractional time evolution.
In ed. R. Hilfer, Applications of Fractional Calculus in
Physics, p. 87, Singapore, (2000). World Scientific.
|
| 51 |
A. Marchaud, Sur les derivees et sur les differences des fonctions de variables
reelles, Journal de Mathematiques Pures et Appliquees. 6,
337, (1927).
|
| 52 |
J. Stafney, Integral representations of fractional powers of infinitesimal
generators, Illinois Journal of Mathematics. 20, 124,
(1976).
|
| 53 |
R. Hilfer, Fitting the excess wing in the dielectric 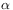 -relaxation of
propylene carbonate, J.Phys.: Condens. Matter. 14, 2297, (2002).
|
| 54 |
R. Hilfer, Experimental evidence for fractional time evolution in glass forming
materials, Chem.Phys. 284, 399, (2002).
|
| 55 |
P. Lunkenheimer, U. Schneider, R. Brand, and A. Loidl, Glassy dynamics,
Contemporary Physics. 41, 15, (2000).
|
| 56 |
U. Schneider, P. Lunkenheimer, R. Brand, and A. Loidl, Broadband dielectric
spectoscopy on glass-forming propylene carbonate, Phys.Rev. E. 59, 6924, (1999).
|
| 57 |
D. Davidson and R. Cole, Dielectric relaxation in glycerol, propylene glycol
and 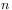 -propanol, J.Chem.Phys. 19, 1484, (1951).
|
| 58 |
R. Hilfer, Analytical representations for relaxation functions of glasses,
J. Noncryst. Solids. 305, 122, (2002).
|
| 59 |
S. Havriliak and S. Negami, A complex plane analysis of 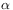-dispersions in
some polymer systems, Journal of Polymer Sciene: Part C. 14,
99–117, (1966).
|
| 60 |
R. Hilfer, 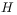 -function representations for stretched exponential relaxation
and non-Debye susceptibilities in glassy systems, Phys.Rev.E. 65, 061510, (2002).
|
| 61 |
R. Hilfer, Y. Luchko, and Z. Tomovski, Operational method for the solution of
fractional differential equations with generalized Riemann-Liouville
fractional derivatives, Fractional Calculus and Applied Analysis. 12, 299, (2009).
|
| 62 |
F. Kremer and A. Schönhals(eds.), Broad Band Dielectric
Spectroscopy. (Springer Verlag, Berlin, 2003).
|
| 63 |
G. Zaslavsky.
Fractional kinetics of hamiltonian chaotic systems.
In ed. R. Hilfer, Applications of Fractional Calculus in
Physics, p. 202, Singapore, (2000). World Scientific.
|
| 64 |
P. Inizan.
Dynamique Fractionnaire Pour Le Chaos Hamiltonien.
PhD thesis, L’Observatoire de Paris, (2011).
|
| 65 |
M. Riesz, L’integrale de Riemann-Liouville et le probleme de Cauchy,
Acta mathematica. 81, 1, (1949).
|
| 66 |
E. Montroll and G. Weiss, Random walks on lattices. II, J. Math. Phys.
6, 167, (1965).
|
| 67 |
M. Barber and B. Ninham, Random and Restricted Walks. (Gordon and Breach
Science Publ., New York, 1970).
|
| 68 |
E. Montroll and H. Scher, Random walks on lattices. IV. Continuous-time
walks and influence of absorbing boundaries, J. Stat. Phys. 9,
101, (1973).
|
| 69 |
R. Hilfer and R. Orbach, Continuous time random walk approach to dynamic
percolation, Chem.Phys. 128, 275, (1988).
|
| 70 |
B. Hughes, Random Walks and Random Environments. vol. 1, (Clarendon
Press, Oxford, 1995).
|
| 71 |
R. Hilfer and L. Anton, Fractional master equations and fractal time random
walks, Phys.Rev.E, Rapid Commun. 51, R848, (1995).
|
| 72 |
R. Hilfer, Exact solutions for a class of fractal time random walks,
Fractals. 3(1), 211, (1995).
|
| 73 |
I. Sokolov, J. Klafter, and A. Blumen, Fractional kinetics, Physics
Today. Nov.2002, 48, (2002).
|
| 74 |
A. V. Balakrishnan, Anomalous diffusion in one dimension, Physica. 132A, 569–580, (1985).
|
| 75 |
M. Shlesinger, Asymptotic solutions of continuous time random walks, J.
Stat. Phys. 10, 421, (1974).
|
| 76 |
R. Hilfer.
On fractional diffusion and its relation with continuous time random
walks.
In eds. A. P. R. Kutner and K. Sznajd-Weron, Anomalous
Diffusion: From Basis to Applications, p. 77, Berlin, (1999). Springer.
|
| 77 |
R. Hilfer, Fractional diffusion based on Riemann-Liouville fractional
derivatives, J.Phys.Chem.B. 104, 3914, (2000).
|
| 78 |
R. Hilfer, On fractional diffusion and continuous time random walks,
Physica A. 329, 35, (2003).
|
| 79 |
A. Compte, Stochastic foundations of fractional dynamics, Phys.Rev. E.
55, 4191, (1996).
|
| 80 |
R. Metzler, J. Klafter, and I. Sokolov, Anomalous transport in external fields:
Continuous time random walks and fractional diffusion equations extended,
Phys.Rev.E. 58, 1621, (1998).
|
| 81 |
R. Metzler, E. Barkai, and J. Klafter, Anomalous diffusion and relaxation close
to equilibrium: A fractional Fokker-Planck equation approach,
Phys.Rev.Lett. 82, 3563, (1999).
|
| 82 |
I. Sokolov, Thermodynamics and fractional fokker-planck equations,
Phys.Rev.E. 63, 056111, (2001).
|
| 83 |
M. Meerschaert, D. Benson, H. Scheffler, and P. Becker-Kern, Governing
equations and solutions of anomalous random walk limits, Phys.Rev.E.
66, 060102, (2002).
|
| 84 |
F. E.Scalas, R.Gorenflo, Uncoupled continuous-time random walks: Solution and
limiting behavior of the master equation, Phys.Rev.E. 69,
011107, (2004).
|
| 85 |
R. Gorenflo, F. Mainardi, D. Moretti, G. Pagnini, and P. Paradisi, Disrete
random walk models for space-time fractional diffusion, Chem.Phys.
284, 521, (2002).
|
| 86 |
G. Zaslavsky, Chaos, fractional kinetics, and anomalous transport,
Phys.Rep. 371, 461, (2002).
|
