Sie sind hier: ICP » R. Hilfer » Publikationen

8 Fractional Time Evolution

[page 214, §1]   
[214.1.1] The induced time evolution is obtained from {\rule[-2.0pt]{0.0pt}{10.0pt}_{{{G}}}\! T} by iteration. [214.1.2] According to its definition in eq. (16) the induced measure preserving transformation {\rule[-2.0pt]{0.0pt}{10.0pt}_{{{G}}}\! T} acts as a convolution in time,

{\rule[-2.0pt]{0.0pt}{10.0pt}_{{{G}}}\! T}\varrho=\varrho*p (17)

where \varrho is a mixed state on ({G},\mathfrak{S}). [214.1.3] Iterating N times gives

{\rule[-2.0pt]{0.0pt}{10.0pt}_{{{G}}}\! T}^{N}\varrho=({\rule[-2.0pt]{0.0pt}{10.0pt}_{{{G}}}\! T}^{{N-1}}\varrho)*p=\varrho*\underbrace{p\dots*p}_{{N\text{~factors}}}=\varrho*p_{N} (18)

where p_{N}(k)=p(k)\dots*p(k) is the probability density of the sum

\mathcal{T}_{N}=\tau _{1}+\dots+\tau _{N} (19)

of N independent and identically with p(k) distributed random recurrence times \tau _{i}. [214.1.4] Then the long time limit N\to\infty for induced measure preserving transformations on subsets of small measure is generally governed by well known local limit theorems for convolutions [42, 43, 44, 45]. [214.1.5] Application to the case at hand yields the following fundamental theorem of fractional dynamics [1, 21]

Theorem 8.1.

Assume that \tau>0 is maximal in the sense that there is no larger \tau for which all recurrence times lie in \tau\mathbb{N}. [214.1.6] Then the following conditions are equivalent:

  1. [214.1.7] Either 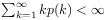\sum _{{k=1}}^{\infty}kp(k)<\infty or there exists a number 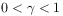0<\gamma<1 such that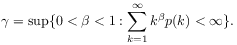

    \gamma=\sup\{ 0<\beta<1:\sum _{{k=1}}^{\infty}k^{\beta}p(k)<\infty\}. (20)

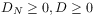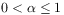  2. [214.1.8] There exist constants D_{N}\geq 0,D\geq 0 and 0<\alpha\leq 1 such that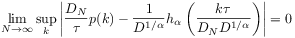

    \lim _{{N\to\infty}}\sup _{k}\left|\frac{D_{N}}{\tau}p(k)-\frac{1}{D^{{1/\alpha}}}h_{\alpha}\left(\frac{k\tau}{D_{N}D^{{1/\alpha}}}\right)\right|=0 (21)

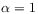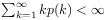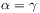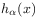    where \alpha=1, if \sum _{{k=1}}^{\infty}kp(k)<\infty, and \alpha=\gamma otherwise. [214.1.9] The function h_{\alpha}(x) vanishes for 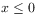x\leq 0, and is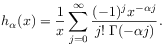

    h_{\alpha}(x)=\frac{1}{x}\sum _{{j=0}}^{\infty}\frac{(-1)^{j}x^{{-\alpha j}}}{j!\;\Gamma(-\alpha j)}. (22)

    for x>0.

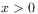[page 215, §0]    [215.0.1] If the limit exists, and is nondegenerate, i.e. D\neq 0, then the rescaling constants D_{N} have the form

D_{N}=\left(N\Lambda(N)\right)^{{1/\alpha}} (23)

where \Lambda(N) is a slowly varying function [46], i.e.

\lim _{{x\to\infty}}\frac{\Lambda(bx)}{\Lambda(x)}=1 (24)

for all b>0.

[215.1.1] The theorem shows that

p_{N}(k)\approx\frac{\tau}{D_{N}D^{{1/\alpha}}}h_{\alpha}\left(\frac{k\tau}{D_{N}D^{{1/\alpha}}}\right) (25)

holds for sufficiently large N. [215.1.2] The asymptotic behaviour of the iterated induced measure preserving transformation {\rule[-2.0pt]{0.0pt}{10.0pt}_{{{G}}}\! T}^{N} for N\to\infty allows to remove the discretization, and to find the induced continuous time evolution on subsets {G}\subset\Gamma. [215.1.3] First, the definition eq. (15) is extended from the arithmetic progression {\dot{s}}-\tau\mathbb{N} to {\dot{t}}\leq{\dot{s}} by linear interpolation. [215.1.4] Let \widetilde{\varrho}({\dot{t}}) denote the extended measure defined for {\dot{t}}\leq{\dot{s}}. [215.1.5] Using eq. (11) and setting

t=D_{N}D^{{1/\alpha}} (26)

the summation in eq. (18) can be approximated for sufficently large N\to\infty by an integral. [215.1.6] Then {\rule[-2.0pt]{0.0pt}{10.0pt}_{{{G}}}\! T}^{N}\widetilde{\varrho}({\dot{s}})\approx{\rule[-2.0pt]{0.0pt}{10.0pt}_{{{G}}}\! T}_{\alpha}^{t}\widetilde{\varrho}({\dot{s}}), where

{\rule[-2.0pt]{0.0pt}{10.0pt}_{{{G}}}\! T}_{\alpha}^{t}\widetilde{\varrho}({\dot{s}})=\int\limits _{0}^{\infty}\widetilde{\varrho}({\dot{s}}-{\dot{t}})h_{\alpha}\left(\frac{{\dot{t}}}{t}\right)\frac{\mathrm{d}{\dot{t}}}{t} (27)

is the induced continuous time evolution.[215.1.7]  {\rule[-2.0pt]{0.0pt}{10.0pt}_{{{G}}}\! T}_{\alpha}^{t} is also called fractional time evolution. [215.1.8] Laplace tranformation shows that {\rule[-2.0pt]{0.0pt}{10.0pt}_{{{G}}}\! T}_{\alpha}^{t} fulfills eq. (5). [215.1.9] It is an example of subordination of semigroups [47, 33, 7, 48]. [215.1.10] Indeed

{\rule[-2.0pt]{0.0pt}{10.0pt}_{{{G}}}\! T}_{\alpha}^{t}=\frac{1}{t}\int\limits _{0}^{\infty}T^{{\dot{t}}}h_{\alpha}\left(\frac{{\dot{t}}}{t}\right)\mathrm{d}{\dot{t}} (28)

where T^{{\dot{t}}} denotes right translations on the interpolated measure. [215.1.11] Because D_{N}\geq 0 and D\geq 0, eq. (26) implies t\geq 0. [215.1.12] As remarked in the introduction, the induced time evolution is in general not a translation (group or semigroup), but a convolution semigroup. [215.1.13] The fundamental classification parameter

\alpha=\alpha(T,{G},\tau) (29)

[page 216, §0]    depends not only on the dynamical rule T(\cdot,{\dot{t}}) and the subset {G}, but also on the discretization time step \tau, i.e. on the time scale of interest.