Sie sind hier: ICP » R. Hilfer » Publikationen

3 Time Evolution of Observables

[209.2.1] Time is commonly considered as the set of Aristotelian time instants {\dot{t}}. [209.2.2] The set of all time instants is represented mathematically by the set of real numbers \mathbb{R}. [209.2.3] Time is “measured” by observing clocks. [209.2.4] Clocks are physical systems. [209.2.5] Let a be an observable quantity (e.g. the position of the sun, the moon or some hand on a watch), and let \mathcal{A} be the set of observables of such a physical system. [209.2.6] A dynamical system is a triple (\mathcal{A},\mathbb{R},T) where \mathcal{A} is the set of observables of a physical system, \mathbb{R} represents time, and the mapping

\displaystyle T\colon\mathcal{A}\times\mathbb{R} \displaystyle\to \displaystyle\mathcal{A}
\displaystyle(a,{\dot{t}}) \displaystyle\mapsto \displaystyle T(a,{\dot{t}}) (1)

is its dynamical rule [25]. [209.2.7] It describes the change of observable quantities with time. [209.2.8] For the dynamical rule T the following properties are postulated:

  1. [209.2.9] For all time instants 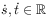{\dot{s}},{\dot{t}}\in\mathbb{R} the dynamical rule obeys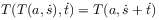

    T(T(a,{\dot{s}}),{\dot{t}})=T(a,{\dot{s}}+{\dot{t}}) (2)

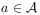    for all a\in\mathcal{A}.

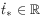  2. [209.2.10] There exists a time instant {\dot{t}}_{*}\in\mathbb{R}, called beginning, such that

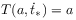
    T(a,{\dot{t}}_{*})=a (3)

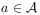    holds for all a\in\mathcal{A}.

  3. [209.2.11] The map 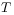T is continuous in time in a suitable topology.

[209.2.12] The set of observables reflects the kinematical structure of the physical system. [209.2.13] The dynamical rule prescribes the time evolution of the system. [page 210, §0]    [210.0.1] Setting {\dot{s}}={\dot{t}}_{*} in eq. (2) and using eq. (3) shows, that either {\dot{t}}_{*}=0 must hold, or else the observable must be time independent. [210.0.2] The time evolution of observables is the one-parameter family \{{\rule[-2.0pt]{0.0pt}{10.0pt}_{{\mathcal{A}}}\! T}^{{\dot{t}}}\} _{{{\dot{t}}\in\mathbb{R}}} of maps {\rule[-2.0pt]{0.0pt}{10.0pt}_{{\mathcal{A}}}\! T}^{{\dot{t}}}\colon\mathcal{A}\to\mathcal{A} defined by

{\rule[-2.0pt]{0.0pt}{10.0pt}_{{\mathcal{A}}}\! T}^{{\dot{t}}}a:=T(a,{\dot{t}}) (4)

for {\dot{t}}\in\mathbb{R}. [210.0.3] The time evolution obeys the group law

{\rule[-2.0pt]{0.0pt}{10.0pt}_{{\mathcal{A}}}\! T}^{{\dot{t}}}{\rule[-2.0pt]{0.0pt}{10.0pt}_{{\mathcal{A}}}\! T}^{{\dot{s}}}={\rule[-2.0pt]{0.0pt}{10.0pt}_{{\mathcal{A}}}\! T}^{{{\dot{s}}+{\dot{t}}}} (5)

for all {\dot{t}},{\dot{s}}\in\mathbb{R}, and the identity law

{\rule[-2.0pt]{0.0pt}{10.0pt}_{{\mathcal{A}}}\! T}(0)=\mathbf{1} (6)

where \mathbf{1} is the identity on \mathcal{A}. [210.0.4] The continuity law requires a topology. [210.0.5] It is usually assumed, that \mathcal{A} is a Banach space with norm \|\cdot\|, and that

\lim _{{{\dot{t}}\to 0^{+}}}\|{\rule[-2.0pt]{0.0pt}{10.0pt}_{{\mathcal{A}}}\! T}^{{\dot{t}}}a-a\|=0 (7)

holds for all a\in\mathcal{A}. [210.0.6] Equations (5),(6) and (7) define a strongly continuous one parameter group of operators \{{\rule[-2.0pt]{0.0pt}{10.0pt}_{{\mathcal{A}}}\! T}^{{\dot{t}}}\} _{{{\dot{t}}\in\mathbb{R}}} on \mathcal{A}, called a flow [26, 27]. [210.0.7] For bounded linear operators strong and weak continuity are equivalent [28].

[210.1.1] Identifying a=a(0) and writing T(a,{\dot{t}})=a({\dot{t}}) the time evolution becomes time translation to the left, i.e.

{\rule[-2.0pt]{0.0pt}{10.0pt}_{{\mathcal{A}}}\! T}^{{\dot{t}}}a({\dot{s}})=a({\dot{s}}+{\dot{t}}) (8)

for all {\dot{t}},{\dot{s}}\in\mathbb{R}. [210.1.2] If the arrow of time is taken into account, then the flow of time is directed, and only the time instants {\dot{t}}\geq 0 after the beginning can occur. [210.1.3] In that case, inverse elements do not exist, and the family \{{\rule[-2.0pt]{0.0pt}{10.0pt}_{{\mathcal{A}}}\! T}^{{\dot{t}}}\} _{{{\dot{t}}\geq 0}} of operators forms only a semigroup [29, 28] instead of a group.