Sie sind hier: ICP » R. Hilfer » Publikationen

2 Classical relaxation models

[1283.4.1] The Debye relaxation model describes the electric relaxation of dipoles after switching an applied electric field [21]. [1283.4.2] The normalized relaxation function f(t), which corresponds to the polarization, obeys the Debye law

\left(\tau\frac{\mbox{${\rm d}$}{}}{\mbox{${\rm d}$}{}t}+1\right)f(t)=0, (1)

[page 1284, §0]    with the relaxation time \tau and initial condition f(0)=1. [1284.0.1] The response function, i.e. the dynamical dielectric susceptibility, \chi is related to the relaxation function via [17]

\chi(t)=-\frac{\mbox{${\rm d}$}{}}{\mbox{${\rm d}$}{}t}f(t). (2)

[1284.0.2] In the following discussions we focus on Laplace transformed quantities. [1284.0.3] We use the Laplace transformation of f(t)

\mbox{${\mathscr L}$}{}\{ f(t)\}(u)=\int _{{0}}^{{\infty}}e^{{-ut}}f(t)\ \mbox{${\rm d}$}{}t, (3)

where u=i\nu and \nu is the frequency. [1284.0.4] Rewriting equation (2) in frequency space and using f(0)=1 leads to

\hat{\chi}(u)=\mbox{${\mathscr L}$}{}\{\chi(t)\}(u)=1-u\mbox{${\mathscr L}$}{}\{ f(t)\}(u)=\frac{1}{1+u\tau}, (4)

the well known Debye susceptibility. [1284.0.5] In experiments one measures not the normalized quantity \hat{\chi}(u), but instead

\varepsilon(u)=(\varepsilon _{{0}}-\varepsilon _{{\infty}})\hat{\chi}(u)+\varepsilon _{{\infty}}, (5)

where \varepsilon _{{0}} and \varepsilon _{{\infty}} are the dynamical susceptibilities at low, respectively high frequencies.

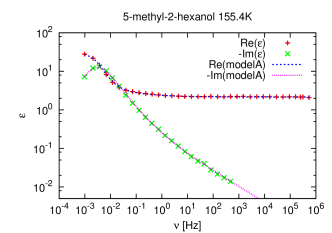
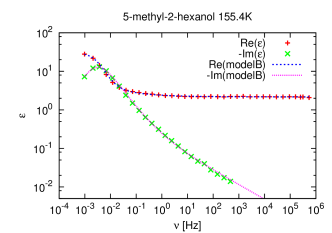
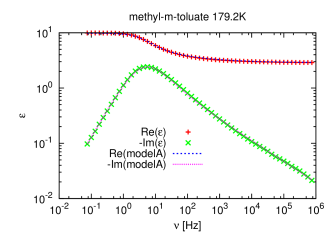
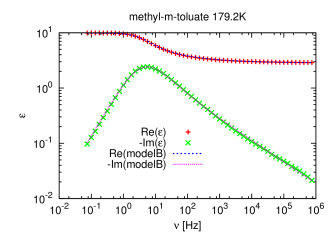
[1284.1.1] The Debye model is not able to describe the experimental data well, because experimental relaxation peaks are broader and asymmetric. [1284.1.2] For this reason other fitting functions were proposed such as the Cole-Cole [22], Cole-Davidson [23] and Havriliak-Negami [16] expressions. [1284.1.3] Their normalized forms have typically 2 or 3 parameters (see table 1) and they were introduced purely phenomenologically to fit the data. [1284.1.4] This can be considered as a drawback. [1284.1.5] These functions with three parameters are able to fit the data over a range of at most 5 decades (Havriliak-Negami). [1284.1.6] To fit a broader frequency range several functions are commonly added. [1284.1.7] A combination of one Havriliak-Negami expression plus one Cole-Cole form results in 6 fit parameters.

functional

form \hat{\chi}(u)

number of

parameters
Cole-Cole 1/(1+(u\tau)^{{\alpha}}) 2
Cole-Davidson 1/(1+u\tau)^{{\alpha}} 2
Havriliak-Negami 1/(1+(u\tau)^{{\alpha}})^{{\gamma}} 3
Table 1: List of traditional fit functions for dielectric spectroscopy data of glass forming materials.
Figure 1: Simultaneous fits of real and imaginary part with model A (left figure) and model B (right figure) for 5-methyl-2-hexanol at 155.4\,{\rm K}. Both models show an excellent fitting capability. The data are from [6].
Figure 2: Simultaneous fits of real and imaginary part with model A (left figure) and model B (right figure) for methyl-m-toluate at 179.2\,{\rm K}. Model A can fit the data over the whole spectral range of 7 decades, which is more than with Havriliak-Negami which uses the same number of fit parameters. With this data we obtain the broadest fit with model A. The data are from [12].