Sie sind hier: ICP » R. Hilfer » Publikationen

5 Temperature dependence of the parameters

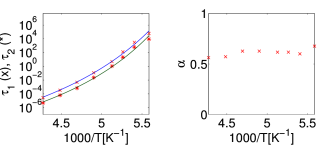
[page 1287, §1]    [1287.1.1] Because the data have been fitted at different temperatures we are able to observe the temperature dependence of the fitting parameters. [1287.1.2] For \tau _{{1}} and \tau _{{2}} we perform Vogel-Tammann-Fulcher fits provided by equation (13). [1287.1.3] From the fits we obtain the Vogel-Fulcher temperatures T_{{\rm VF1}} and T_{{\rm VF2}} as well as the fragility parameters D_{{1}} and D_{{2}} for the relaxation times \tau _{{1}} and \tau _{{2}} for model A and model B (see Table 2).

material model T_{{\rm VF1}} T_{{\rm VF2}} D_{{1}} D_{{2}} \tau _{{01}} \tau _{{02}}
5-methyl-2-hexanol A 89.2\,{\rm K} 92.1\,{\rm K} 25.5 22.1 3.53\times 10^{{-13}}\,{\rm s} 7\times 10^{{-14}}\,{\rm s}
5-methyl-2-hexanol B 88.3\,{\rm K} 101.6\,{\rm K} 26.3 15.3 5.21\times 10^{{-13}}\,{\rm s} 5.77\times 10^{{-12}}\,{\rm s}
methyl-m-toluate A 71.2\,{\rm K} 71.2\,{\rm K} 93.2 93.2 4.35\times 10^{{-28}}\,{\rm s} 1.54\times 10^{{-28}}\,{\rm s}
methyl-m-toluate B 67.2\,{\rm K} 85.6\,{\rm K} 102.2 53.6 9.0\times 10^{{-28}}\,{\rm s} 1.13\times 10^{{-22}}\,{\rm s}
glycerol A 127.8\,{\rm K} 131.5\,{\rm K} 17.1 14.9 3.7\times 10^{{-14}}\,{\rm s} 3.23\times 10^{{-14}}\,{\rm s}
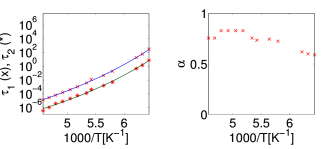
glycerol B 152.7\,{\rm K} 137.8\,{\rm K} 6.68 11.9 2.9\times 10^{{-10}}\,{\rm s} 2.15\times 10^{{-13}}\,{\rm s}
Table 2: List of the fit parameters T_{{\rm VF}}, D and \tau _{{0}} for various materials.

[1287.2.1] For all fits we see a temperature dependence of the relaxation times \tau _{{1}} and \tau _{{2}} (Fig. 4 - Fig. 6) that follows the Vogel-Tammann-Fulcher fitting function remarkably well. [1287.2.2] The relaxation times also show a clear downward trend as the temperature increases, which confirms that \tau, \tau _{{1}} and \tau _{{2}} are physically meaningful and can be interpreted as relaxation times even tough they appear with a non-integer power in equations (11) and (12).

[1287.3.1] The parameters \alpha, \alpha _{{1}} and \alpha _{{2}} also show a temperature dependence. [1287.3.2] In the case of 5-methyl-2-hexanol (Fig. 4) there is an increase of \alpha with temperature until a plateau near \alpha=1 is reached. [1287.3.3] This effect comes from the decreasing slope of the excess wing with increasing temperature. [1287.3.4] In the fitting function of model A this behavior can be achieved by increasing \alpha. [1287.3.5] For the same material there is an apparent increase of \alpha _{{2}} between 154\,{\rm K} (6.49\,{\rm K}^{{-1}}) and 287\,{\rm K} (3.48\,{\rm K}^{{-1}}) which has the same origin as the increase in \alpha in model A. [1287.3.6] By increasing \alpha _{{2}} the excess wing becomes less steep. [1287.3.7] The plateau at 190\,{\rm K} (5.26\,{\rm K}^{{-1}}) and above comes from the fact that the fits at those temperatures are done mainly for the \alpha-peak, because the excess wing is not visible.

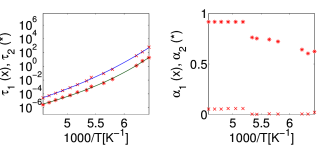
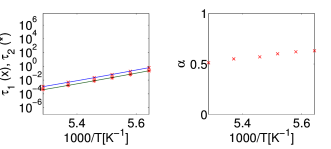
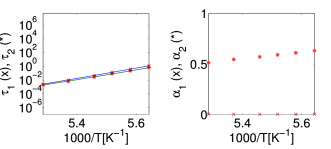
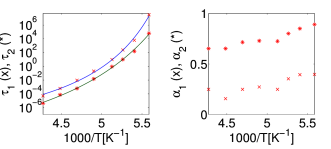
[1287.4.1] For methyl-m-toluate and glycerol there is also a clear temperature dependence of \alpha, \alpha _{{1}} and \alpha _{{2}} (Fig. 5 and Fig. 6). [1287.4.2] The trend is however reversed in comparison to 5-methyl-2-hexanol. [1287.4.3] This comes from the increasing slope of the excess wing with increasing temperature. [1287.4.4] This behavior can be achieved in the fit functions by decreasing \alpha, respectively \alpha _{{2}}.

Figure 4: Temperature dependence of the fitting parameters \tau _{{1}} (crosses), \tau _{{2}} (stars) and \alpha for 5-methyl-2-hexanol for model A (left two panels). Temperature dependence of the fitting parameters \tau _{{1}} (crosses), \tau _{{2}} (stars), \alpha _{{1}} (crosses) and \alpha _{{2}} (stars) for model B (right two panels). The solid lines are Vogel-Tammann-Fulcher fits (see eq. (13)) whose parameters are listed in Table 2.
Figure 5: Temperature dependence of the fitting parameters \tau _{{1}} (crosses), \tau _{{2}} (stars) and \alpha for methyl-m-toluate for model A (left two panels). Temperature dependence of the fitting parameters \tau _{{1}} (crosses), \tau _{{2}} (stars), \alpha _{{1}} (crosses) and \alpha _{{2}} (stars) for model B (right two panels). The solid lines are Vogel-Tammann-Fulcher fits (see eq. (13)) whose parameters are listed in Table 2.
Figure 6: Temperature dependence of the fitting parameters \tau _{{1}} (crosses), \tau _{{2}} (stars) and \alpha for glycerol for model A (left two panels). Temperature dependence of the fitting parameters \tau _{{1}} (crosses), \tau _{{2}} (stars), \alpha _{{1}} (crosses) and \alpha _{{2}} (stars) for model B (right two panels). The solid lines are Vogel-Tammann-Fulcher fits (see eq. (13)) whose parameters are listed in Table 2.