Sie sind hier: ICP » R. Hilfer » Publikationen

3 Fractional relaxation models

[1284.2.1] In this work we use a generalized form of the Debye relaxation model from eq. (1). [1284.2.2] It is based on the theory of fractional time evolutions for macroscopic states of many body systems first proposed in equation (5.5) in [24] and subsequently elaborated in [25, 26, 27, 28, 29, 30, 17, 31, 32, 33, 34]. [1284.2.3] As discussed in [30, 17] composite fractional time evolutions are expected near the glass transition. [1284.2.4] Such time evolutions give rise to generalized Debye laws of the form of model A:

\left(\tau _{{1}}\mbox{${\rm D}$}{}+\tau _{{2}}^{{\alpha}}\mbox{${\rm D}$}{}^{{\alpha}}+1\right)f(t)=0 (6)

or model B:

\left(\tau _{{1}}\mbox{${\rm D}$}{}+\tau _{{1}}^{{\alpha _{{1}}}}\mbox{${\rm D}$}{}^{{\alpha _{{1}}}}+\tau _{{2}}^{{\alpha _{{2}}}}\mbox{${\rm D}$}{}^{{\alpha _{{2}}}}+1\right)f(t)=0, (7)

where the parameters obey 0<\alpha,\alpha _{{1}},\alpha _{{2}}<1, \alpha _{{1}}>\alpha _{{2}} and the relaxation times \tau _{1},\tau _{2}>0 are positive. [1284.2.5] Here the symbols \tau _{{1}}\mbox{${\rm D}$}{}+\tau _{{2}}^{{\alpha}}\mbox{${\rm D}$}{}^{{\alpha}}, respectively \tau _{{1}}\mbox{${\rm D}$}{}+\tau _{{1}}^{{\alpha _{{1}}}}\mbox{${\rm D}$}{}^{{\alpha _{{1}}}}+\tau _{{2}}^{{\alpha _{{2}}}}\mbox{${\rm D}$}{}^{{\alpha _{{2}}}} are the infinitesimal generators of composite fractional semigroups [page 1285, §0]    with \mbox{${\rm D}$}{}^{{\alpha}} being a generalized fractional Riemann-Liouville derivative of order \alpha and almost any type [29, 35]. [1285.0.1] If \mbox{${\rm D}$}{}^{{\nu}} represents a classical fractional Riemann-Liouville derivative of order \nu then its definition reads (with \nu\in\mathbb{R}^{{+}})

\displaystyle\mbox{${\rm D}$}{}^{{\nu}}f(t) \displaystyle=\mbox{${\rm D}$}{}^{{\lceil\nu\rceil}}\mbox{${\rm I}$}{}^{{\mu}}f(t) (8)
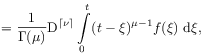\displaystyle=\frac{1}{\Gamma(\mu)}\mbox{${\rm D}$}{}^{{\lceil\nu\rceil}}\int\limits _{{0}}^{{t}}(t-\xi)^{{\mu-1}}f(\xi)\ \mbox{${\rm d}$}{}\xi, (9)
\displaystyle\mu+\nu=\lceil\nu\rceil,\quad t>0,

where \lceil\nu\rceil is the smallest integer greater or equal \nu, \Gamma the gamma function and \mbox{${\rm D}$}{}^{{\lceil\nu\rceil}}=\mbox{${\rm d}$}{}^{{\lceil\nu\rceil}}/\mbox{${\rm d}$}{}t^{{\lceil\nu\rceil}}.

[1285.1.1] The Laplace transform of the fractional Riemann-Liouville derivative is [36]

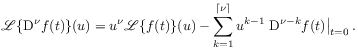\mbox{${\mathscr L}$}{}\{\mbox{${\rm D}$}{}^{{\nu}}f(t)\}(u)=u^{{\nu}}\mbox{${\mathscr L}$}{}\{ f(t)\}(u)-\sum _{{k=1}}^{{\lceil\nu\rceil}}u^{{k-1}}\left.\mbox{${\rm D}$}{}^{{\nu-k}}f(t)\right|_{{t=0}}. (10)

[page 1286, §1]    [1286.1.1] With these definitions the Laplace transformation of equations (6) and (7) gives with relation (2) the normalized dielectric susceptibilities of model A

\hat{\chi}_{{\rm A}}(u)=\frac{\displaystyle{1+\tau _{{2}}^{{\alpha}}u^{{\alpha}}}}{\displaystyle{\tau _{{1}}u+\tau _{{2}}^{{\alpha}}u^{{\alpha}}+1}} (11)

and model B

\hat{\chi}_{{\rm B}}(u)=\frac{\displaystyle{1+\tau _{{1}}^{{\alpha _{{1}}}}u^{{\alpha _{{1}}}}+\tau _{{2}}^{{\alpha _{{2}}}}u^{{\alpha _{{2}}}}}}{\displaystyle{\tau _{{1}}u+\tau _{{1}}^{{\alpha _{{1}}}}u^{{\alpha _{{1}}}}+\tau _{{2}}^{{\alpha _{{2}}}}u^{{\alpha _{{2}}}}+1}}. (12)

[1286.1.2] These results apply also for other types of generalized Riemann-Liouville fractional derivatives introduced in [30, 17].

[1286.2.1] The functions from equations (11) and (12) are used to fit the dielectric spectroscopy data of 5-methyl-2-hexanol, glycerol and methyl-m-toluate. [1286.2.2] Real and imaginary part are fitted simultaneously with the parameters \alpha, \alpha _{{1}}, \alpha _{{2}}, \tau _{{1}} and \tau _{{2}}.

[1286.3.1] Additionally we fit the temperature dependent relaxation times \tau _{{1}} and \tau _{{2}} with the Vogel-Tammann-Fulcher function

\tau=\tau _{{0}}\exp\left(\frac{DT_{{\rm VF}}}{T-T_{{\rm VF}}}\right), (13)

where T is the absolute temperature, \tau _{{0}} a material parameter, D the fragility and T_{{\rm VF}} the Vogel-Fulcher temperature. [1286.3.2] The fit parameters are \tau _{{0}}, D and T_{{\rm VF}}.