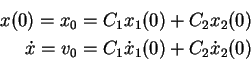Next: Das ebene mathematische Pendel
Up: Anfangswertprobleme
Previous: Anfangswertprobleme
Bereits 1895 stellte H.v. Helmholtz fest, dass das menschliche
Ohr Frequenzen wahrnimmt, die gar nicht in den
Schallwellen vorkommen.
Das Trommelfell ist eine schwingende Masse, (genauer eine
trichterförmige Membran), die durch die Schallwellen der Luft in
Schwingung versetzt wird und sie so über Hammer, Amboss und
Steigbügel auf das Innenohr überträgt. Man hofft, dass sich das
Trommelfell völlig passiv verhält, das heißt möglichst so
wie ein harmonischer Oszillator. Diese Beobachtung von Helmholtz legt
nahe, dass die Herleitung von Gleichung (![[*]](file:/mnt/bison/local/lib/latex2html/icons/crossref.gif) ) nicht
allgemein genug war.
Allgemeiner könnte die Newtonsche Bewegungsgleichung lauten:
) nicht
allgemein genug war.
Allgemeiner könnte die Newtonsche Bewegungsgleichung lauten:
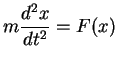 |
(5.2) |
wobei 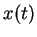 die Auslenkung des Trommelfells aus der Ruhelage,
die Auslenkung des Trommelfells aus der Ruhelage, 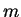 die
Masse des Trommelfells, und
die
Masse des Trommelfells, und 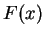 die Rückstellkraft auf das
Trommelfell in Abhängigkeit von seiner Auslenkung ist. Nun nehmen
wir ohne große Beschränkung der Allgemeinheit an, dass sich
die Rückstellkraft auf das
Trommelfell in Abhängigkeit von seiner Auslenkung ist. Nun nehmen
wir ohne große Beschränkung der Allgemeinheit an, dass sich
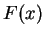 in einer Taylerreihe um
in einer Taylerreihe um 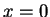 entwickeln läßt, also
entwickeln läßt, also
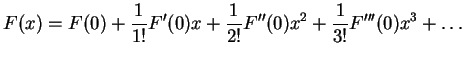 |
(5.3) |
Im Gleichgewicht muss offenbar stets
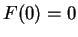 |
(5.4) |
gelten, und damit es eine rückstellende Kraft ist muss stets
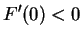 |
(5.5) |
gelten. Setzt man
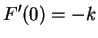 |
(5.6) |
mit 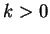 und
und
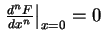 für alle
für alle 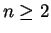 so folgt sofort (
so folgt sofort (![[*]](file:/mnt/bison/local/lib/latex2html/icons/crossref.gif) ).
).
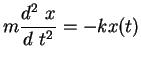 |
(5.7) |
Nennen wir 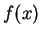 treibende Kraft, die von den Schallwellen eines
Sinustons auf das Trommelfell ausgeübt wird, dann lautet die
einfache Trommelfellgleichung:
treibende Kraft, die von den Schallwellen eines
Sinustons auf das Trommelfell ausgeübt wird, dann lautet die
einfache Trommelfellgleichung:
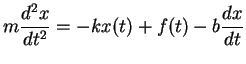 |
(5.8) |
oder mit
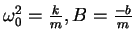 :
:
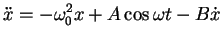 |
(5.9) |
wenn man die treibende Kraft
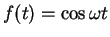 |
(5.10) |
und
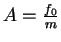 setzt. Dies ist eine lineare Gleichung. Nach
einem Einschwingvorgang müsste das Trommelfell mit der Frequenz
setzt. Dies ist eine lineare Gleichung. Nach
einem Einschwingvorgang müsste das Trommelfell mit der Frequenz
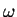 der treibenden Kraft schwingen. Nun ist aber die Annahme in
(
der treibenden Kraft schwingen. Nun ist aber die Annahme in
(![[*]](file:/mnt/bison/local/lib/latex2html/icons/crossref.gif) ), die äquivalent ist zum Hookeschen Gesetz nur
näherungsweise gültig. Im allgemeinen können auch höhere
Ableitungen der Rückstellkraft
), die äquivalent ist zum Hookeschen Gesetz nur
näherungsweise gültig. Im allgemeinen können auch höhere
Ableitungen der Rückstellkraft
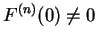 von Null
verschieden sein. Eine erste
Annahme wäre
von Null
verschieden sein. Eine erste
Annahme wäre
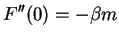 |
(5.11) |
Das führt auf die nichtlineare Trommelfellgleichung von Helmholtz
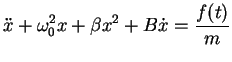 |
(5.12) |
Die Nichtlinearität koppelt die über
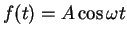 angeregte Schwingung an die
anderen Vielfachen der Anregungsfrequenz
angeregte Schwingung an die
anderen Vielfachen der Anregungsfrequenz 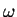 .
.
Allgemeine Lösung von (![[*]](file:/mnt/bison/local/lib/latex2html/icons/crossref.gif) )
)
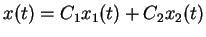 |
(5.13) |
Dabei ist 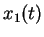 die allgemeine Lösung der homogenen Gleichung
die allgemeine Lösung der homogenen Gleichung
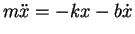 |
(5.14) |
die bereits in Abschnitt ![[*]](file:/mnt/bison/local/lib/latex2html/icons/crossref.gif) diskutiert wurde. Es
ist eine exponentiell abklingende harmonische Schwingung mit der
Frequenz
diskutiert wurde. Es
ist eine exponentiell abklingende harmonische Schwingung mit der
Frequenz 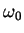
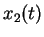
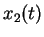 ist eine spezielle Lösung der
Gleichung (
ist eine spezielle Lösung der
Gleichung (![[*]](file:/mnt/bison/local/lib/latex2html/icons/crossref.gif) ) und zwar
) und zwar
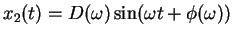 |
(5.15) |
wobei
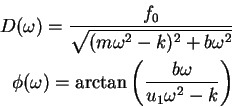
Die Konstanten 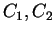 werden durch die Anfangsbedingungen
werden durch die Anfangsbedingungen
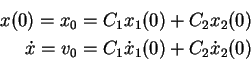
festgelegt.
Man beachte das Resonanzphänomen.




Next: Das ebene mathematische Pendel
Up: Anfangswertprobleme
Previous: Anfangswertprobleme
© R.Hilfer et al., ICA-1, Univ. Stuttgart
28.6.2002
![]() ) nicht
allgemein genug war.
Allgemeiner könnte die Newtonsche Bewegungsgleichung lauten:
) nicht
allgemein genug war.
Allgemeiner könnte die Newtonsche Bewegungsgleichung lauten:
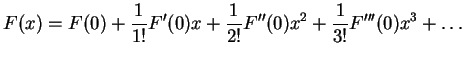
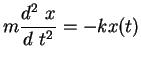
![]() die allgemeine Lösung der homogenen Gleichung
die allgemeine Lösung der homogenen Gleichung
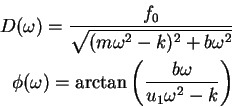
![]() werden durch die Anfangsbedingungen
werden durch die Anfangsbedingungen