V.C Single Phase Fluid Flow

V.C.1 Permeability and Darcy’s Law

The permeability is the most important physical property of a porous medium in much the same way as the porosity is its most important geometrical property. Some authors define porous media as media with a nonvanishing permeability [2]. Permeability measures quantitatively the ability of a porous medium to conduct fluid flow. The permeability tensor ${\bf K}$ relates the macroscopic flow density $\overline{\bf v}$ to the applied pressure gradient $\mbox{\boldmath$\nabla$}P$ or external field ${\bf F}$ through

$\overline{\bf v}=\frac{{\bf K}}{\eta}({\bf F}-\mbox{\boldmath$\nabla$}P)$

(5.54)

where $\eta$ is the dynamic viscosity of the fluid. $\overline{\bf v}$ is the flow rate per unit area of cross section. Equation (5.54) is known as Darcy’s law.

The permeability has dimensions of an area, and it is measured in units of Darcy (d). If the pressure is measured in physical atmospheres one has 1d=0.9869 $\mu$ m ${}^{2}$ while 1d=1.0197 $\mu$ m ${}^{2}$ if the pressure is measured in technical atmospheres. To within practical measuring accuracy one may often assume 1d= $10^{{-12}}$ m ${}^{2}$ . An important question arising from the fact that ${\bf K}$ is dimensionally an area concerns the interpretation of this area or length scale in terms of the underlying geometry. This fundamental question has recently found renewed interest [318, 43, 319, 320, 170, 172, 4]. Unfortunately most answers proposed in these discussions [319, 318, 320, 4] give a dynamical rather than geometrical interpretation of this length scale. The traditional answer to this basic problem is provided by hydraulic radius theory [3, 2]. It gives a geometrical interpretation which is based on the capillary models of section III.B.1, and it will be discussed in the next section.

The permeability does not appear in the microscopic Stokes or Navier-Stokes equations. Darcy’s law and with it the permeability concept can be derived from microscopic Stokes flow equations using homogenization techniques [268, 269, 270, 38, 321, 271] which are asymptotic expansions in the ratio of microscopic to macroscopic length scales. The derivation will be given in section V.C.3 below.

The linear Darcy law holds for flows at low Reynolds numbers in which the driving forces are small and balanced only by the viscous forces. Various nonlinear generalizations of Darcy’s law have also been derived using homogenization or volume averaging methods [268, 1, 269, 322, 321, 38, 271, 323, 324, 325]. If a nonlinear Darcy law governs the flow in a given experiment this would appear in the measurement as if the permeability becomes velocity dependent. The linear Darcy law breaks down also if the flow becomes too slow. In this case interactions between the fluid and the pore walls become important. Examples occur during the slow movement of polar liquids or electrolytes in finely porous materials with high specific internal surface.

V.C.2 Hydraulic Radius Theory

The hydraulic radius theory or Carman-Kozeny model is based on the geometrical models of capillary tubes discussed above in section III.B.1. In such capillary models the permeability can be obtained exactly from the solution of the Navier-Stokes equation (4.9) in the capillary. Consider a cylindrical capillary tube of length $L$ and radius $a$ directed along the $x$ -direction. The velocity field ${\bf v}({\bf r})$ for creeping laminar flow is of the form ${\bf v}({\bf r})=v(r){\bf e}_{x}$ where ${\bf e}_{x}$ denotes a unit vector along the pipe, and $r$ measures the distance from the center of the pipe. The pressure has the form $P({\bf r})=P(x){\bf e}_{x}$ . Assuming “no slip” boundary conditions, $v(a)=0$ , at the tube walls one obtains for $v(r)$ the familiar Hagen-Poiseuille result [326]

$\displaystyle P(x)$	$\displaystyle=$	$\displaystyle P(0)-(P(0)-P(L))\frac{x}{L}$		(5.55)
$\displaystyle v(r)$	$\displaystyle=$	$\displaystyle\frac{P(0)-P(L)}{4\eta L}(a^{2}-r^{2})$		(5.56)

with a parabolic velocity and linear pressure profile. The volume flow rate $Q$ is obtained through integration as

$Q=\int _{0}^{a}v(r)2\pi r\; dr=\frac{\pi a^{4}}{8\eta}\frac{P(0)-P(L)}{L}.$

(5.57)

Consider now the capillary tube model of section III.B.1 with a cubic sample space $\mathbb{S}$ of sidelength $L$ . The pore space $\mathbb{P}$ consists of $N$ nonintersecting capillary tubes of radii $a_{i}$ and lengths $L_{i}$ distributed according to a joint probability density $\Pi(a,L)$ . The pressure drop must then be calculated over the length $L_{i}$ and thus the right hand side of (5.57) is multiplied by a factor $L/L_{i}$ . Because the tubes are nonintersecting the volume flow $Q_{i}$ through each of the tubes can be added to give the macroscopic volume flow rate per unit area $\overline{\bf v}=(1/L^{2})\sum _{{i=1}}^{N}Q_{i}$ . Thus the permeability of the capillary tube model is simply additive, and it reads

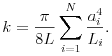$k=\frac{\pi}{8L}\sum _{{i=1}}^{N}\frac{a_{i}^{4}}{L_{i}}.$

(5.58)

Dimensional analysis of (5.58), (3.58) and (3.59) shows that $kS^{2}/\phi^{3}$ is dimensionless. Averaging (5.58) as well as (3.58) and (3.59) for the porosity and specific internal surface of the capillary tube model yields the relation

$\left\langle k\right\rangle=\frac{C}{2}\frac{\left\langle\phi\right\rangle^{3}}{\left\langle S\right\rangle^{2}}$

(5.59)

where the mixed moment ratio

$C=L^{2}\left\langle\frac{a^{4}}{L}\right\rangle\frac{\left\langle aL\right\rangle^{2}}{\left\langle a^{2}L\right\rangle^{3}}$

(5.60)

is a dimensionless number, and the angular brackets denote as usual the average with respect to $\Pi(a,L)$ .

The hydraulic radius theory or Carman-Kozeny model is obtained from a mean field approximation which assumes $\left\langle f(x)\right\rangle\approx f(\left\langle x\right\rangle)$ . The approximation becomes exact if the distribution is sharply peaked or if $L_{i}=L$ and $a_{i}=a$ for all $N$ . With this approximation the average permeability $\left\langle k\right\rangle$ may be rewritten in terms of the average hydraulic radius $\left\langle R_{H}\right\rangle$ defined in (3.66) as

$\left\langle k\right\rangle\approx\frac{\left\langle\phi\right\rangle}{2\left\langle\mathcal{T}\right\rangle^{2}}\frac{\left\langle\phi\right\rangle^{2}}{\left\langle S\right\rangle^{2}}\approx\frac{\left\langle\phi\right\rangle}{2\left\langle\mathcal{T}\right\rangle^{2}}\left\langle\frac{\phi^{2}}{S^{2}}\right\rangle\approx\frac{\left\langle\phi\right\rangle\left\langle R_{H}\right\rangle^{2}}{2\left\langle\mathcal{T}\right\rangle^{2}}\approx\frac{\left\langle\phi\right\rangle\left\langle a\right\rangle^{2}}{8\left\langle\mathcal{T}\right\rangle^{2}}$

(5.61)

where $\left\langle\mathcal{T}\right\rangle=\left\langle L\right\rangle/L$ is the average of the tortuosity defined above in (3.62). Equation (5.61) is one of the main results of hydraulic radius theory. The permeability is expressed as the square of an average hydraulic radius $\left\langle R_{H}\right\rangle$ , which is related to the average “pore width” as $\left\langle R_{H}\right\rangle=\left\langle a\right\rangle/2$ .

It must be stressed that hydraulic radius theory is not exact even for the simple capillary tube model because in general $\left\langle R_{H}\right\rangle\neq\left\langle\phi\right\rangle/\left\langle S\right\rangle$ and $C\neq 1/\left\langle\mathcal{T}\right\rangle^{2}$ . However, interesting exact relations for the average permeability can be obtained from (5.59) and (5.60) in various special cases without employing the mean field approximation of hydraulic radius theory. If the tube radii and lengths are independent then the distribution factorizes as $\Pi(a,L)=\Pi _{a}(a)\Pi _{L}(L)$ . In this case the permeability may be written as

$\left\langle k\right\rangle=\frac{1}{2}\frac{\left\langle 1/\mathcal{T}\right\rangle}{\left\langle\mathcal{T}\right\rangle}\frac{\left\langle a^{4}\right\rangle\left\langle a\right\rangle^{2}}{\left\langle a^{2}\right\rangle^{3}}\frac{\left\langle\phi\right\rangle^{3}}{\left\langle S\right\rangle^{2}}=\frac{\left\langle\phi\right\rangle}{8}\frac{\left\langle 1/\mathcal{T}\right\rangle}{\left\langle\mathcal{T}\right\rangle}\frac{\left\langle a^{4}\right\rangle}{\left\langle a^{2}\right\rangle}$

(5.62)

where $\left\langle\mathcal{T}\right\rangle$ is the average of the tortuosity factor defined in (3.62). The last equality interprets $\left\langle k\right\rangle$ in terms of the microscopic effective cross section $\left\langle a^{4}\right\rangle/\left\langle a^{2}\right\rangle$ determined by the variance and curtosis of the distribution of tube radii. Further specialization to the cases $L_{i}=l$ or $a_{i}=a$ is readily carried out from these results.

Finally it is of interest to consider also the capillary slit model of section III.B.1. The model assumes again a cubic sample of side length $L$ containing a pore space consisting of parallel slits with random widths governed by a probability density $\Pi(b)$ . For flat planes without undulations the analogue of tortuosity is absent. The average permeability is obtained in this case as

$\left\langle k\right\rangle=\frac{1}{3}\frac{\left\langle b^{3}\right\rangle}{\left\langle b\right\rangle^{3}}\frac{\left\langle\phi\right\rangle^{3}}{\left\langle S\right\rangle^{2}}$

(5.63)

which has the same form as (5.59) with a constant $C=\left\langle b^{3}\right\rangle/\left\langle b\right\rangle^{3}$ . The prefactor $1/3$ is due to the different shape of the capillaries, which are planes rather than tubes.

V.C.3 Derivation of Darcy’s Law from Stokes Equation

The previous section has shown that Darcy’s law arises in the capillary models. This raises the question whether it can be derived more generally. The present section shows that Darcy’s law can be obtained from Stokes equation for a slow flow. It arises to lowest order in an asymptotic expansion whose small parameter is the ratio of microscopic to macroscopic length scales.

Consider the stationary and creeping (low Reynolds number) flow of a Newtonian incompressible fluid through a porous medium whose matrix is assumed to be rigid. The microscopic flow through the pore space $\mathbb{P}$ is governed by the stationary Stokes equations for the velocity ${\bf v}({\bf r})$ and pressure $P({\bf r})$

$\displaystyle\eta\Delta{\bf v}({\bf r})+{\bf F}-\mbox{\boldmath$\nabla$}P({\bf r})$	$\displaystyle=$	$\displaystyle 0$		(5.64)
$\displaystyle\mbox{\boldmath$\nabla$}^{T}\cdot{\bf v}({\bf r})$	$\displaystyle=$	$\displaystyle 0$		(5.65)

inside the pore space, $\mathbb{P}\ni{\bf r}$ , with no slip boundary condition

${\bf v}({\bf r})={\bf 0}$

(5.66)

for ${\bf r}\in\partial\mathbb{P}$ . The body force ${\bf F}$ and the dynamic viscosity $\eta$ are assumed to be constant.

The derivation of Darcy’s law assumes that the pore space $\mathbb{P}$ has a characteristic length scale $l$ which is small compared to some macroscopic scale $L$ . The microscopic scale $l$ could be the diameter of grains, the macroscale $L$ could be the diameter of the sample $\mathbb{S}$ or some other macroscopic length such as the diameter of a measurement cell or the wavelength of a seismic wave. The small ratio $\varepsilon=l/L$ provides a small parameter for an asymptotic expansion. The expansion is constructed by assuming that all properties and fields can be written as functions of two new space variables ${\bf x},{\bf y}$ which are related to the original space variable ${\bf r}$ as ${\bf x}={\bf r}$ and ${\bf y}={\bf r}/\varepsilon$ . All functions $f({\bf r})$ are now replaced with functions $f({\bf x},{\bf y})$ and the slowly varying variable ${\bf x}$ is allowed to vary independently of the rapidly varying variable ${\bf y}$ . This requires to replace the gradient according to

$\mbox{\boldmath$\nabla$}f({\bf r})=\mbox{\boldmath$\nabla$}f({\bf r},{\bf r}/\varepsilon)=\mbox{\boldmath$\nabla$}_{{\bf x}}f({\bf x},{\bf y})+\frac{1}{\varepsilon}\mbox{\boldmath$\nabla$}_{{\bf y}}f({\bf x},{\bf y})$

(5.67)

and the Laplacian is replaced similarly. The velocity and pressure are now expanded in $\varepsilon$ where the leading orders are chosen such that the solution is not reduced to the trivial zero solution and the problem remains physically meaningful. In the present case this leads to the expansions [268, 280, 271]

$\displaystyle{\bf v}({\bf r})$	$\displaystyle=$	$\displaystyle\varepsilon^{2}{\bf v}_{0}({\bf x},{\bf y})+\varepsilon^{3}{\bf v}_{1}({\bf x},{\bf y})+...$		(5.68)
$\displaystyle P({\bf r})$	$\displaystyle=$	$\displaystyle P_{0}({\bf x},{\bf y})+\varepsilon P_{1}({\bf x},{\bf y})+...$		(5.69)

where ${\bf x}={\bf r}$ and ${\bf y}={\bf r}/\varepsilon$ . Inserting into (5.64), (5.65) and (5.66) yields to lowest order in $\varepsilon$ the system of equations

$\displaystyle\mbox{\boldmath$\nabla$}_{{\bf y}}P_{0}({\bf x},{\bf y})$	$\displaystyle=$	$\displaystyle 0\quad\mbox{in }\mathbb{P}$	(5.70)
$\displaystyle\mbox{\boldmath$\nabla$}_{{\bf y}}^{T}\cdot{\bf v}_{0}$	$\displaystyle=$	$\displaystyle 0\quad\mbox{in }\mathbb{P}$	(5.71)
$\displaystyle\eta\Delta _{{\bf y}}{\bf v}_{0}-\mbox{\boldmath$\nabla$}_{{\bf y}}P_{1}-\mbox{\boldmath$\nabla$}_{{\bf x}}P_{0}+{\bf F}$	$\displaystyle=$	$\displaystyle 0\quad\mbox{in }\mathbb{P}$	(5.72)
$\displaystyle\mbox{\boldmath$\nabla$}_{{\bf x}}^{T}\cdot{\bf v}_{0}+\mbox{\boldmath$\nabla$}_{{\bf y}}^{T}\cdot{\bf v}_{1}$	$\displaystyle=$	$\displaystyle 0\quad\mbox{in }\mathbb{P}$	(5.73)
$\displaystyle{\bf v}_{0}$	$\displaystyle=$	$\displaystyle{\bf 0}\quad\mbox{on }\partial\mathbb{P}$	(5.74)

in the fast variable ${\bf y}$ . It follows from the first equation that $P_{0}({\bf x},{\bf y})$ depends only on the slow variable ${\bf x}$ , and thus it appears as an additional external force for the determination of the dependence of ${\bf v}_{0}({\bf x},{\bf y})$ on ${\bf y}$ from the remaining equations. Because the equations are linear the solution ${\bf v}_{0}({\bf x},{\bf y})$ has the form

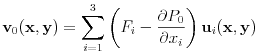${\bf v}_{0}({\bf x},{\bf y})=\sum _{{i=1}}^{3}\left(F_{i}-\frac{\partial P_{0}}{\partial x_{i}}\right){\bf u}_{i}({\bf x},{\bf y})$

(5.75)

where the three vectors ${\bf u}_{i}({\bf x},{\bf y})$ (and the scalars $Q_{i}({\bf x},{\bf y})$ ) are the solutions of the three systems ( $i=1,2,3$ )

$\displaystyle\mbox{\boldmath$\nabla$}_{{\bf y}}^{T}\cdot{\bf u}_{i}$	$\displaystyle=$	$\displaystyle 0\quad\mbox{in }\mathbb{P}$	(5.76)
$\displaystyle\eta\Delta _{{\bf y}}{\bf u}_{i}-\mbox{\boldmath$\nabla$}_{{\bf y}}Q_{i}-{\bf e}_{{y_{i}}}$	$\displaystyle=$	$\displaystyle 0\quad\mbox{in }\mathbb{P}$	(5.77)
$\displaystyle{\bf u}_{i}$	$\displaystyle=$	$\displaystyle{\bf 0}\quad\mbox{on }\partial\mathbb{P}$	(5.78)

and ${\bf e}_{{y_{i}}}$ is a unit vector in the direction of the $y_{i}$ -axis.

It is now possible to average ${\bf v}_{0}$ over the fast variable ${\bf y}$ . The spatial average over a convex set $\mathbb{K}$ is defined as

$\overline{\bf v}_{0}({\bf x};\mathbb{K})=\frac{1}{V(\mathbb{K})}\int{\bf v}_{0}({\bf x},{\bf y})\chi\rule[-4.3pt]{0.0pt}{8.6pt}_{{\mathbb{K}}}({\bf x},{\bf y})d^{3}{\bf y}$

(5.79)

where $\mathbb{K}$ is centered at ${\bf x}$ and $\chi\rule[-4.3pt]{0.0pt}{8.6pt}_{{\mathbb{K}}}({\bf x},{\bf y})=\chi\rule[-4.3pt]{0.0pt}{8.6pt}_{{\mathbb{K}}}({\bf r},{\bf r}/\varepsilon)$ equals $1$ or $0$ depending upon whether ${\bf r}\in\mathbb{K}$ or not. The dependence on the averaging region $\mathbb{K}$ has been indicated explicitly. Using the notation of (2.20) the average over all space is obtained as the limit $\lim _{{s\rightarrow\infty}}\overline{\bf v}_{0}({\bf x};s\mathbb{K})=\overline{\bf v}_{0}({\bf x})$ . The function $P_{0}$ need not to be averaged as it depends only on the slow variable ${\bf x}$ . If ${\bf v}_{0}$ is constant then $\overline{{\bf v}_{0}}({\bf x})={\bf v}_{0}\overline{\phi}({\bf x})$ which is known as the law of Dupuit-Forchheimer [1]. Averaging (5.75) gives Darcy’s law (5.54) in the form

$\overline{\bf v}_{0}({\bf x};\mathbb{K})=\frac{{\bf K}({\bf x};\mathbb{K})}{\eta}\left({\bf F}-\mbox{\boldmath$\nabla$}_{{\bf x}}P_{0}({\bf x})\right)$

(5.80)

where the components $k_{{ij}}({\bf x};\mathbb{K})=({\bf K}({\bf x};\mathbb{K}))_{{ij}}$ of the permeability tensor ${\bf K}$ are expressed in terms of the solutions ${\bf u}_{j}({\bf x};\mathbb{K})$ to (5.76)–(5.78) within the region $\mathbb{K}$ as

$({\bf K}({\bf x};\mathbb{K}))_{{ij}}=\left(\overline{{\bf u}_{j}}({\bf x};\mathbb{K})\right)_{i}.$

(5.81)

The permeability tensor is symmetric and positive definite [268]. Its dependence on the configuration of the pore space $\mathbb{P}$ and the averaging region $\mathbb{K}$ have been made explicit because they will play an important role below. For isotropic and strictly periodic or stationary media the permeability tensor reduces to a constant independent of ${\bf x}$ . For (quasi-)periodic microgeometries or (quasi-)stationary random media averaging eq. (5.73) leads to the additional macroscopic relation

$\mbox{\boldmath$\nabla$}_{{\bf x}}^{T}\cdot\overline{\bf v}_{0}({\bf x};\mathbb{K})=0.$

(5.82)

Equations (5.80) and (5.82) are the macroscopic laws governing the microscopic Stokes flow obeying (5.64)–(5.66) to leading order in $\varepsilon=l/L$ .

The importance of the homogenization technique illustrated here in a simple example lies in the fact that it provides a systematic method to obtain the reference problem for an effective medium treatment.

Many of the examples for transport and relaxation in porous media listed in chapter IV can be homogenized using a similar technique [268]. The heterogeneous elliptic equation (4.2) is of particular interest. The linear Darcy flow derived in this section can be cast into the form of (4.2) for the pressure field. The permeability tensor may still depend on the slow variable ${\bf x}$ , and it is therefore of interest to iterate the homogenization procedure in order to see whether Darcy’s law becomes again modified on larger scales. This question is discussed next.

V.C.4 Iterated Homogenization

The permeability ${\bf K}({\bf x})$ for the macroscopic Darcy flow was obtained from homogenizing the Stokes equation by averaging the fast variable ${\bf y}$ over a region $\mathbb{K}$ . The dependence on the slow variable ${\bf x}$ allows for macroscopic inhomogeneities of the permeability. This raises the question whether the homogenization may be repeated to arrive at an averaged description for a much larger megascopic scale.

If (5.80) is inserted into (5.82) and ${\bf F}=0$ is assumed the equation for the macroscopic pressure field becomes

$\nabla^{T}\cdot({\bf K}({\bf x})\nabla P({\bf x}))=0$

(5.83)

which is identical with (4.2). The equation must be supplemented with boundary conditions which can be obtained from the requirements of mass and momentum conservation at the boundary of the region for which (5.83) was derived. If the boundary marks a transition to a region with different permeability the boundary conditions require continuity of pressure and normal component of the velocity.

Equation (5.83) holds at length scales $L$ much larger than the pore scale $l$ , and much larger than diameter of the averaging region $\mathbb{K}$ . To homogenize it one must therefore consider length scales $\mathcal{L}$ much larger than $l$ such that

$l\ll L\ll\mathcal{L}$

(5.84)

is fulfilled. The ratio $\delta=L/\mathcal{L}$ is then a small parameter in terms of which the homogenization procedure of the previous section can be iterated. The pressure is expanded in terms of $\delta$ as

$P({\bf x})=P_{0}({\bf s},{\bf z})+\delta P_{1}({\bf s},{\bf z})+...$

(5.85)

where now ${\bf s}={\bf x}$ is the slow variable, and ${\bf z}={\bf s}/\delta$ is the rapidly varying variable. Assuming that the medium is stationary, i.e. that ${\bf K}({\bf z})$ does not depend on the slow variable ${\bf s}$ , the result becomes [268, 280, 271]

$\nabla^{T}\cdot(\overline{{\bf K}}\nabla P_{0}({\bf s}))=0$

(5.86)

where $P_{0}({\bf s})$ is the first term in the expansion of the pressure which is independent of ${\bf z}$ , and the tensor $\overline{{\bf K}}$ has components

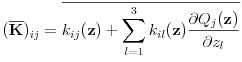$(\overline{{\bf K}})_{{ij}}=\overline{k_{{ij}}({\bf z})+\sum _{{l=1}}^{3}k_{{il}}({\bf z})\frac{\partial Q_{j}({\bf z})}{\partial z_{l}}}$

(5.87)

given in terms of three scalar fields $Q_{j}(j=1,2,3)$ which are obtained from solving an equation of the form

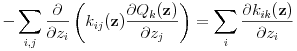$-\sum _{{i,j}}\frac{\partial}{\partial z_{i}}\left(k_{{ij}}({\bf z})\frac{\partial Q_{k}({\bf z})}{\partial z_{j}}\right)=\sum _{i}\frac{\partial k_{{ik}}({\bf z})}{\partial z_{i}}$

(5.88)

analogous to (5.76)–(5.78) in the homogenization of Stokes equation.

If the assumption of strict stationarity is relaxed the averaged permeability depends in general on the slow variable, and the homogenized equation (5.86) has then the same form as the original equation (5.83). This shows that the form of the macroscopic equation does not change under further averaging. This highlights the importance of the averaged permeability as a key element of every macroscopically homogeneous description. Note however that the averaged tensor $\overline{{\bf K}}$ may have a different symmetry than the original permeability. If ${\bf K}({\bf x})=k({\bf x}){\bf 1}$ is isotropic ( ${\bf 1}$ denotes the unit matrix) then $\overline{{\bf K}}$ may become anisotropic because of the second term appearing in (5.87).

V.C.5 Network Model

Consider a porous medium described by equation (5.83) for Darcy flow with a stationary and isotropic local permeability function ${\bf K}({\bf x})=k({\bf x}){\bf 1}$ . The expressions (5.87) and (5.88) for the the effective permeability tensor $\overline{{\bf K}}$ are difficult to use for general random microstructures. Therefore it remains necessary to follow the strategy outlined in section V.A.2 and to discretize (5.83) using a finite difference scheme with lattice constant $L$ . As before it is assumed that $l\ll L\ll\mathcal{L}$ where $l$ is the pore scale and $\mathcal{L}$ is the system size. The discretization results in the linear network equations (5.5) for a regular lattice with lattice constant $L$ .

To make further progress it is necessary to specify the local permeabilities. A microscopic network model of tubes results from choosing the expression

$k(a,\ell,L)=\frac{\pi}{8L}\frac{a^{4}}{\ell}.$

(5.89)

for a cylindrical capillary tube of radius $a$ and length $\ell$ in a region of size $L$ . The parameters $a$ and $\ell$ must obey the geometrical conditions $a\leq L/2$ and $\ell\geq L$ . In the resulting network model each bond represents a winding tube with circular cross section whose diameter and length fluctuate from bond to bond. The network model is completely specified by assuming that the local geometries specified by $a$ and $\ell$ are independent and identically distributed random variables with joint probability density $\Pi(a,\ell)$ . Note that the probability density $\Pi(a,\ell)$ depends also on the discretization length through the constraints $a\leq L/2$ and $\ell\geq L$ .

Using the effective medium approximation to the network equations the effective permeability $\overline{k}$ for this network model is the solution of the selfconsistency equation

$\int _{L}^{\infty}\int _{0}^{{L/2}}\frac{\pi a^{4}-8L\ell\overline{k}}{\pi a^{4}+16L\ell\overline{k}}\Pi(a,\ell)\; dad\ell=0$

(5.90)

where the restrictions on $a$ and $\ell$ are reflected in the limits of integration. In simple cases, as for binary or uniform distributions, this equation can be solved analytically, in other cases it is solved numerically. The effective medium prediction agrees well with an exact solution of the network equations [231]. The behaviour of the effective permeability depends qualitatively on the fraction $p$ of conducting tubes defined as

$p=1-\lim _{{\varepsilon\rightarrow 0}}\int _{0}^{\varepsilon}\Pi(a)\; da$

(5.91)

where $\Pi(a)=\int _{L}^{\infty}\Pi(a,\ell)d\ell$ . For $p>1/3$ the permeability is positive while for $p<1/3$ it vanishes. At $p=p_{c}=1/3$ the network has a percolation transition. Note that $p\neq\overline{\phi}$ is not related to the average porosity.

V.C.6 Local Porosity Theory

Consider, as in the previous section, a porous medium described by equation (5.83) for Darcy flow with a stationary and isotropic local permeability function ${\bf K}({\bf x})=k({\bf x}){\bf 1}$ . A glance at section III shows that the one cell local geometry distribution defined in (3.45) are particularly well adapted to the discretization of (5.83). As before the discretization employs a cubic lattice with lattice constant $L$ and cubic measurement cells $\mathbb{K}$ and yields a local geometry distribution $\mu(\phi,S;\mathbb{K})$ . It is then natural to use the Carman equation (5.59) locally because it is often an accurate description as illustrated in Figure 23.

Figure 23: Log-log plot of the permeability coefficient $\relax kg\rho/\relax\eta$ , where $\relax k$ is the permeability, $g$ the acceleration of gravity, $\rho$ the fluid density and $\relax\eta$ the fluid viscosity against the combination $\relax S/(\phi)^{{3/2}}$ of porosity $\relax\phi$ and specific surface $\relax S$ for sands and basalt split.[ [Reproduced with permission from [1] J. Schopper, “Porosität und Permeabilität,” in Landolt-Börnstein: Physikalische Eigenschaften der Gesteine (K.-H. Hellwege, ed.), vol. V/1a, (Berlin), p. 184, Springer, 1982, Copyright Springer Verlag 1982.]

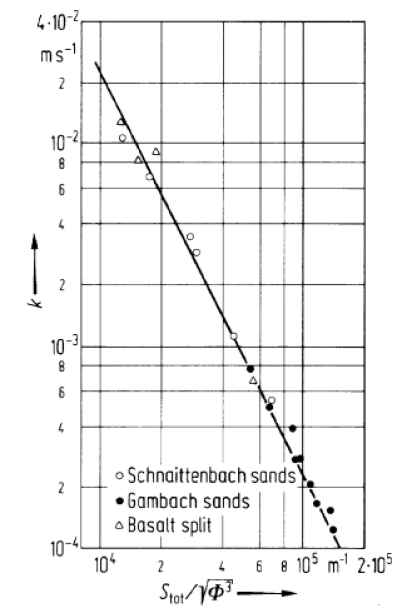
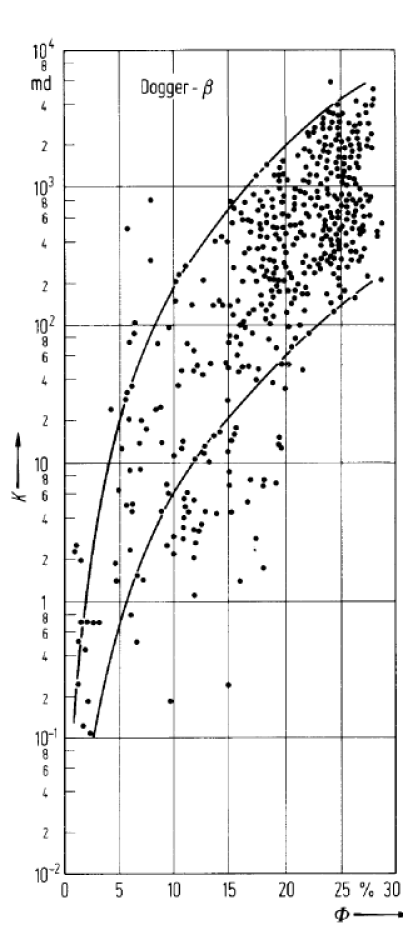
The straight line in Figure 23 corresponds to equation (5.59). The local percolation probabilities defined in section III.A.5.d complete the description. Each local geometry is characterized by its local porosity, specific internal surface and a binary random variable indicating whether the geometry is percolating or not. The selfconsistent effective medium equation now reads

$\int _{0}^{\infty}\int _{0}^{1}\frac{3C\phi^{3}\lambda(\phi,S;\mathbb{K})\mu(\phi,S;\mathbb{K})}{C\phi^{3}+4S^{2}\overline{k}}\; d\phi\; dS=1$

(5.92)

for the effective permeability $\overline{k}$ . The control parameter for the underlying percolation transition was given in (3.47) as

$p(L)=\int _{0}^{\infty}\int _{0}^{1}\lambda(\phi,S;\mathbb{K})\mu(\phi,S;\mathbb{K})d\phi dS$

(5.93)

and it gives the total fraction of percolating local geometries. If the quantity

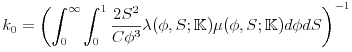$k_{0}=\left(\int _{0}^{\infty}\int _{0}^{1}\frac{2S^{2}}{C\phi^{3}}\lambda(\phi,S;\mathbb{K})\mu(\phi,S;\mathbb{K})d\phi dS\right)^{{-1}}$

(5.94)

is finite then the solution to (5.92) is given approximately as

$\overline{k}\approx k_{0}(p-p_{c})$

(5.95)

for $p>p_{c}=1/3$ and as $\overline{k}=0$ for $p<p_{c}$ . This result is analogous to (5.48) for the electrical conductivity. Note that the control parameter for the underlying percolation transition differs from the bulk porosity $p\neq\overline{\phi}$ .

To study the implications of (5.92) it is necessary to supply explicit expressions for the local geometry distribution $\mu(\phi,S;L)$ . Such an expression is provided by the local porosity reduction model reviewed in section III.B.6. Writing the effective medium approximation for the number $\overline{n}$ defined in (3.87) and using equations (3.86) and (3.88) it has been shown that the effective permeability may be written approximately as [170]

$\overline{k}=\overline{\phi}^{\beta}\lambda(\overline{\phi})$

(5.96)

where the exponent $\beta$ depends on the porosity reduction factor $r$ and the type of consolidation model characterized by (3.88) as

$\beta=(3-2\alpha)\frac{\ln r}{r-1}.$

(5.97)

If all local geometries are percolating, i.e. if $\lambda=1$ , then the effective permeability depends algebraically on the bulk porosity $\overline{\phi}$ with a strongly nonuniversal exponent $\beta$ . This dependence will be modified if the local percolation probability $\lambda(\overline{\phi})$ is not constant. The large variability is consistent with experience from measuring permeabilities in experiment. Figure 24 demonstrates the large data scatter seen in experimental results. While in general small permeabilities correlate with small porosities the correlation is not very pronounced.

Figure 24: Logarithmic plot of permeability versus porosity for Dogger- $\beta$ (Jurassic) sandstone. [Reproduced with permission from [1] J. Schopper, “Porosität und Permeabilität,” in Landolt-Börnstein: Physikalische Eigenschaften der Gesteine (K.-H. Hellwege, ed.), vol. V/1a, (Berlin), p. 184, Springer, 1982, Copyright Springer Verlag 1982.]

Author:	R. Hilfer
originally published in:	Advances in Chemical Physics 92, 299-424 (1996)
originally submitted:	May 9th, 1995