Sie sind hier: ICP » R. Hilfer » Publikationen

III Finite ensemble scaling

[67.2.1.1] The quantity of main interest for finite ensemble scaling [21, 22, 23] is the macroscopic ensemble sum X_{{MN}}(\mbox{\boldmath$\vec{\varphi}$\unboldmath}) given by (2.19). [67.2.1.2] The idea is to neglect completely its microscopic definition (2.18) in terms of cell variables, and to consider the mesoscopic block variables X_{{MN}}(\mbox{\boldmath$\vec{\varphi}$\unboldmath}(\mbox{\boldmath$\vec{y}$\unboldmath})) as a starting point. [67.2.1.3] The univariate probability distribution of the ensemble variable is defined as

P_{{X_{{MN}}}}(x)=\mbox{Prob}\{ X_{{MN}}(\mbox{\boldmath$\vec{\varphi}$\unboldmath})\leq x\}. (3.1)

[67.2.1.4] Because the ensemble limit automatically generates independent and identically distributed block variables X_{{MN}}(\mbox{\boldmath$\vec{\varphi}$\unboldmath}(\mbox{\boldmath$\vec{y}$\unboldmath}_{j})) the standard theory of stable laws [27, 28] can be applied. [67.2.1.5] It yields the existence and uniqueness of limiting distributions for the linearly renormalized ensemble sums

Z_{{MN}}(\mbox{\boldmath$\vec{\varphi}$\unboldmath})=\frac{X_{{MN}}(\mbox{\boldmath$\vec{\varphi}$\unboldmath})-C_{N}}{D_{N}}=\frac{\sum _{{j=1}}^{{N}}X_{{MN}}(\mbox{\boldmath$\vec{\varphi}$\unboldmath}(\mbox{\boldmath$\vec{y}$\unboldmath}_{j}))-C_{N}}{D_{N}} (3.2)

where D_{N}>0 and C_{N} are real numbers. [67.2.1.6] Remember that this holds for sums of arbitrary block variables independent of their microscopic definition. [67.2.1.7] The index M serves only as a reminder for the fact that the ensemble limit is used.

[page 68, §0]    [68.1.0.1] The distribution function P_{{Z_{{MN}}}}(x) for Z_{{MN}}(\mbox{\boldmath$\vec{\varphi}$\unboldmath}) is given in terms of P_{{X_{{MN}}}}(x) as P_{{X_{{MN}}}}(D_{N}x+C_{N}) and it is thus sufficient to consider P_{{X_{{MN}}}}(x). [68.1.0.2] The (weak) ensemble limit of these probability distribution functions

\lim _{{\genfrac{}{}{0.0pt}{}{M,N\rightarrow\infty}{N/M=c}}}P_{{X_{{MN}}}}(D_{N}x+C_{N})=H(x;\varpi _{X}(c),\zeta _{X}(c),C(c),D(c)) (3.3)

exists if and only if H(x;\varpi _{X}(c),\zeta _{X}(c),C(c),D(c)) is a stable distribution function whose characteristic function

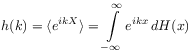h(k)=\langle e^{{ikX}}\rangle=\int _{{-\infty}}^{{\infty}}e^{{ikx}}\, dH(x) (3.4)

has the form

h(k;\varpi _{X},\zeta _{X},C,D)=\exp\left(iCk-D|k|^{{\varpi _{X}}}e^{{\frac{i\pi}{2}(1-|1-\varpi _{X}|)\zeta _{X}{\rm sgn}k}}\right) (3.5)

for \varpi _{X}\neq 1 and

h(k;1,\zeta _{X},C,D)=\exp\left(iCk-D|k|(1-i\zeta _{X}\frac{2}{\pi}\,{\rm sgn}\, k\,\log|k|)\right) (3.6)

for \varpi _{X}=1. [68.1.0.3] The c-dependence of the parameters \varpi _{X}(c),\zeta _{X}(c),C(c),D(c) has been suppressed to shorten the notation. [68.1.0.4] The parameters \varpi _{X},\zeta _{X},C,D obey

\begin{array}[]{c}\ \ \ \ 0<\varpi _{X}\leq 2\\ \ -1\leq\zeta _{X}\leq 1\\ -\infty<C<\infty\\ 0\leq D.\end{array} (3.7)

[68.1.0.5] If the limit exists, and D\neq 0, the constants D_{N} must have the form

D_{N}=(N\Lambda(N))^{{1/\varpi _{X}}} (3.8)

where \Lambda(N) is a slowly varying function [28], i.e.

\lim _{{x\rightarrow\infty}}\frac{\Lambda(bx)}{\Lambda(x)}=1 (3.9)

for all b>0.

[68.1.0.6] The forms (3.5) and (3.6) of the limiting characteristic functions imply the following scaling relations for the stable probability densities h(x;\varpi _{X},\zeta _{X},C,D). [68.1.0.7] If \varpi _{X}\neq 1 then

h(x;\varpi _{X},\zeta _{X},C,D)=D^{{-1/\varpi _{X}}}h((x-C)D^{{-1/\varpi _{X}}};\varpi _{X},\zeta _{X},0,1) (3.10)

holds, while for \varpi _{X}=1 one has

h(x;\varpi _{X},\zeta _{X},C,D)=D^{{-1}}h((x-C)D^{{-1}}-2\frac{\zeta _{X}}{\pi}\log D;\varpi _{X},\zeta _{X},0,1). (3.11)

[68.2.0.1] The parameters C and D correspond to the centering and the width of the distribution.

[68.2.1.1] Strictly stable probability densities (i.e. those with \varpi _{X}\neq 1) are conveniently written in terms of Mellin transforms [29, 30]. [68.2.1.2] This representation is useful for computations and involves the general class of H-functions [31, 32]. [68.2.1.3] For 1<\varpi _{X}<2 corresponding to equilibrium phase transitions two cases are distinguished. [68.2.1.4] If |\zeta _{X}|\neq 1 then [30, 22]

h(x;\varpi _{X},\zeta _{X},0,1)=\frac{1}{\varpi _{X}}H^{{11}}_{{22}}\left(x\left|\begin{array}[]{cc}(1-1/\varpi _{X},1/\varpi _{X})&(1-\varrho,\varrho)\\ (0,1)&(1-\varrho,\varrho)\end{array}\right.\right) (3.12)

where \varrho=\frac{1}{2}-\frac{\zeta _{X}}{\varpi _{X}}+\frac{\zeta _{X}}{2} and the definition of the general H-function H_{{PQ}}^{{mn}} is given in the appendix. [68.2.1.5] If |\zeta _{X}|=1 then for 1<\varpi _{X}<2

h(x;\varpi _{X},\pm 1,0,1)=\frac{1}{\varpi _{X}}H^{{10}}_{{11}}\left(x\left|\begin{array}[]{cc}(1-1/\varpi _{X},1/\varpi _{X})\\ (0,1)\end{array}\right.\right) (3.13)

[68.2.1.6] Similar expressions hold for 0<\varpi _{X}<1[30, 22]. [68.2.1.7] The special case \varpi _{X}=2 of the general limit theorem (3.3) is the central limit theorem [28] and in this case the stable probability density

h(x;2,\zeta _{X},C,D)=\frac{1}{\sqrt{4D\pi}}e^{{-(x-C)^{2}/(4D)}} (3.14)

is the Gaussian distribution with mean C and variance \sigma^{2}=4D. [68.2.1.8] Note that the right hand side is independent of \zeta _{X} in this case. [68.2.1.9] Another special case expressible in terms of elementary functions is \varpi _{X}=1,\zeta _{X}=0 where

h(x;1,0,C,D)=\frac{1}{\pi D}\frac{D^{2}}{D^{2}+(x-C)^{2}} (3.15)

is the Cauchy distribution centered at C and having width D.

[68.2.2.1] For sufficiently large but finite N=(L/\xi)^{d} equation (3.3) implies that the distribution function of ensemble variables may be approximately written as

P_{{X_{{MN}}}}(x)=\left\{\begin{array}[]{rl}R(x,M,N,c)H\left(\dfrac{x-C_{N}}{D_{N}};\varpi _{X},\zeta _{X},C,D\right)&\text{\ \ \ \ :\ \ \ \ for\ \ }x\leq 0\\ &\\ 1-R(x,M,N,c)\left(1-H\left(\dfrac{x-C_{N}}{D_{N}};\varpi _{X},\zeta _{X},C,D\right)\right)&\text{\ \ \ \ :\ \ \ \ for\ \ }x>0\end{array}\right. (3.16)

[page 69, §0]    involving a nonuniversal cutoff functionR(x,M,N,c) such that R(0,M,N,c)=1 and\lim _{{x\rightarrow\pm\infty}}R(x,M,N,c)=0 for all M,N<\infty. In the ensemble limit the cutoff function must obey

\lim _{{\genfrac{}{}{0.0pt}{}{M,N\rightarrow\infty}{N/M=c}}}R(x;M,N,c)=1, (3.17)

for all x and c as a result of equation (3.3). [69.1.0.1] Note that equation (3.17) does not hold for the finite size scaling limit. [69.1.0.2] Instead Table I implies that for the finite size scaling limit

\lim _{{\genfrac{}{}{0.0pt}{}{L,\xi\rightarrow\infty}{L/\xi=c}}}R(x;M,N,N/M)=R(x;\infty,c^{d},0) (3.18)

if the limit exists, and where now c=L/\xi. [69.1.0.3] The function R(x;\infty,(L/\xi)^{d},0) may in general differ from unity, and thus the finite size scaling limit may involve a nonuniversal cutoff function which is absent in the finite ensemble limit.

[69.1.1.1] Wherever possible equation (3.16) will be abbreviated as

P_{{X_{{MN}}}}(x)\approx H\left(\frac{x-C_{N}}{D_{N}};\varpi _{X},\zeta _{X},C,D\right). (3.19)

to shorten the equations. [69.1.1.2] If the centering constants are now chosen as

C_{N}=\left\{\begin{array}[]{rl}-D_{N}C&\text{\ \ \ \ :\ \ \ \ for\ \ }\varpi _{X}\neq 1\\ -D_{N}(C+\frac{2}{\pi}\zeta _{X}D\,\log D)&\text{\ \ \ \ :\ \ \ \ for\ \ }\varpi _{X}=1\end{array}\right. (3.20)

then using equations (3.10),(3.11) and (3.8) the basic finite ensemble scaling result [21, 22]

p_{{X_{{MN}}}}(x)\approx h(x;\varpi _{X},\zeta _{X},0,DN\Lambda(N)) (3.21)

is obtained for the probability density function p_{{X_{{MN}}}}(x) of suitably centered and renormalized ensemble sums. [69.1.1.3] The approximate result (3.21) has formed the basis for the statistical mechanical classification of phase transitions [21, 22].

[69.1.2.1] From the basic result (3.21) the scaling form for the probability density of ensemble averaged block variables \overline{X}_{{MN}}(\mbox{\boldmath$\vec{\varphi}$\unboldmath})=X_{{MN}}(\mbox{\boldmath$\vec{\varphi}$\unboldmath})/(MN) is readily obtained using eq. (3.10) as

\overline{p}_{{\overline{X}_{{MN}}}}(x)\approx\frac{(L/\xi)^{{d(1-(1/\varpi _{X}))}}}{\left(D\Lambda((L/\xi)^{d})\right)^{{1/\varpi _{X}}}}\; h\left(\frac{x\:(L/\xi)^{{d(1-(1/\varpi _{X}))}}}{\left(D\Lambda((L/\xi)^{d})\right)^{{1/\varpi _{X}}}};\varpi _{X},\zeta _{X},0,1\right). (3.22)

[69.1.2.2] Setting X=\Psi this result is found to be distinctly different from equation (1.3). This shows that finite ensemble scaling (3.22) and finite size scaling (1.3) are not equivalent.