Sie sind hier: ICP » R. Hilfer » Publikationen

Appendix B Derivation of equation (7.5)

[76.3.1.1] By virtue of the symmetry relation (6.5) the integral in (7.4) may be written as

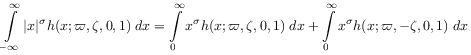\int _{{-\infty}}^{{\infty}}|x|^{\sigma}h(x;\varpi,\zeta,0,1)\; dx=\int _{{0}}^{{\infty}}x^{\sigma}h(x;\varpi,\zeta,0,1)\; dx+\int _{{0}}^{{\infty}}x^{\sigma}h(x;\varpi,-\zeta,0,1)\; dx (B.1)

The definition (A.1) implies the general formula [32]

\int _{0}^{\infty}x^{{s-1}}\hbox{$\displaystyle H^{{mn}}_{{PQ}}\left(ax\left|\begin{array}[]{ccc}(a_{1},A_{1})&...&(a_{P},A_{P})\\ (b_{1},B_{1})&...&(b_{Q},B_{Q})\end{array}\right.\right)\, dx=$}a^{{-s}}\,\frac{\prod _{{j=1}}^{{m}}\Gamma(b_{j}+B_{j}s)\,\prod _{{j=1}}^{{n}}\Gamma(1-a_{j}-A_{j}s)}{\prod _{{j=m+1}}^{{Q}}\Gamma(1-b_{j}-B_{j}s)\,\prod _{{j=n+1}}^{{P}}\Gamma(a_{j}+A_{j}s)} (B.2)

by virtue of the Mellin inversion theorem. [76.3.1.2] Specializing to the case at hand

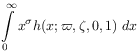\displaystyle\int _{{0}}^{{\infty}}x^{\sigma}h(x;\varpi,\zeta,0,1)\; dx \displaystyle=\frac{1}{\varpi}\int _{0}^{\infty}x^{\sigma}\; H^{{11}}_{{22}}\left(x\left|\begin{array}[]{cc}(1-1/\varpi,1/\varpi)&(1-\varrho,\varrho)\\ (0,1)&(1-\varrho,\varrho)\end{array}\right.\right)\, dx (B.3)
\displaystyle=\frac{\Gamma(\sigma+1)\Gamma(-\sigma/\varpi)}{\varpi\Gamma(1+\varrho\sigma)\Gamma(-\varrho\sigma)} (B.4)

where \varrho=\frac{1}{2}-\frac{\zeta}{\varpi}+\frac{\zeta}{2}. [76.3.1.3] Using \Gamma(x)\Gamma(-x)=-\pi/(x\sin(\pi x)) and the functional equation for the \Gamma-function gives

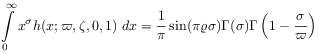\int _{{0}}^{{\infty}}x^{\sigma}h(x;\varpi,\zeta,0,1)\; dx=\frac{1}{\pi}\sin(\pi\varrho\sigma)\Gamma(\sigma)\Gamma\left(1-\frac{\sigma}{\varpi}\right) (B.5)

which inserted into (B.1) readily yields the desired result (7.5).