Sie sind hier: ICP » R. Hilfer » Publikationen

Appendix A Definition of 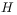H-functions

[76.1.1.2] The general H-function is defined as the inverse Mellin transform [32]

\hbox{$\displaystyle H^{{mn}}_{{PQ}}\left(z\left|\begin{array}[]{ccc}(a_{1},A_{1})&...&(a_{P},A_{P})\\ (b_{1},B_{1})&...&(b_{Q},B_{Q})\end{array}\right.\right)=$}\frac{1}{2\pi i}\int _{{\mathcal{C}}}\frac{\prod _{{j=1}}^{{m}}\Gamma(b_{j}-B_{j}s)\,\prod _{{j=1}}^{{n}}\Gamma(1-a_{j}+A_{j}s)}{\prod _{{j=m+1}}^{{Q}}\Gamma(1-b_{j}+B_{j}s)\,\prod _{{j=n+1}}^{{P}}\Gamma(a_{j}-A_{j}s)}\; z^{{s}}\, ds (A.1)

where the contour {\mathcal{C}} runs from c-i\infty to c+i\infty separating the poles of \Gamma(b_{j}-B_{j}),\;(j=1,...,m) from those of \Gamma(1-a_{j}+A_{j}s),\;(j=1,...,n). [76.1.1.3] Empty products are interpreted as unity. [76.1.1.4] The integers m,n,P,Q satisfy 0\leq m\leq Q and 0\leq n\leq P. [76.1.1.5] The coefficients A_{j} and B_{j} are positive real numbers and the complex parameters a_{j},b_{j} are such that no poles in the integrand coincide. [76.1.1.6] If

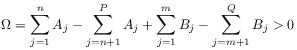\Omega=\sum _{{j=1}}^{{n}}A_{j}-\sum _{{j=n+1}}^{{P}}A_{j}+\sum _{{j=1}}^{{m}}B_{j}-\sum _{{j=m+1}}^{{Q}}B_{j}>0 (A.2)

then the integral converges absolutely and defines the H-function in the sector |{\rm arg}z|\!\!<\Omega\pi/2. [76.2.0.1] The H-function is also well defined when either

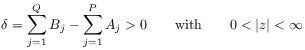\delta=\sum _{{j=1}}^{{Q}}B_{j}-\sum _{{j=1}}^{{P}}A_{j}>0\ \ \ \ \ \ \text{with}\ \ \ \ \ \ 0<|z|<\infty (A.3)

or

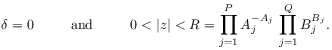\delta=0\ \ \ \ \ \ \ \ \text{and}\ \ \ \ \ \ \ \ 0<|z|<R=\prod _{{j=1}}^{{P}}A_{{j}}^{{-A_{j}}}\,\prod _{{j=1}}^{{Q}}B_{j}^{{B_{j}}}. (A.4)

[76.3.0.1] The H-function is a generalization of Meijers G-function and many of the known special functions are special cases of it.