Sie sind hier: ICP » R. Hilfer » Publikationen

IV Finite size scaling

[69.1.3.1] This section discusses the implications of finite ensemble scaling for finite size scaling at a critical point. [69.1.3.2] Contrary to finite ensemble scaling the theory of finite size scaling includes the strongly correlated microscopic cell variables into the theoretical consideration. [69.2.0.1] This can be done in two ways. [69.2.0.2] Thermodynamic finite size scaling concentrates on the thermodynamic fluctuations within the ensemble, while statistical mechanical (or fieldtheoretical) finite size scaling focusses on the correlation functions on the block level. [69.2.0.3] The distinction appears already in equations (1.1) and (1.2). [69.2.0.4] The general identification of thermodynamics as the infinite volume limit of statistical mechanics implies a relation between the two parts which is at the origin of hyperscaling relations.

IV.A Thermodynamic finite size scaling

[69.2.1.1] The thermodynamic method of reintroducing the strongly correlated cell variables is to to use the definition of block variables (2.18) and to define

Z_{{MN}}(\mbox{\boldmath$\vec{\varphi}$\unboldmath})=\frac{X_{{MN}}(\mbox{\boldmath$\vec{\varphi}$\unboldmath})-C_{{MN}}}{D_{{MN}}}=\frac{\sum _{{j=1}}^{{N}}\sum _{{i=1}}^{{M}}X_{{MN}}(\mbox{\boldmath$\vec{\varphi}$\unboldmath}(\mbox{\boldmath$\vec{y}$\unboldmath}_{j}+\mbox{\boldmath$\vec{x}$\unboldmath}_{i}))-C_{{MN}}}{D_{{MN}}} (4.1)

as a double sum over correlated microscopic cell variables. [69.2.1.2] Although the microscopic variables are strongly correlated inside the blocks they remain uncorrelated at separations larger than \xi. [69.2.1.3] Therefore the property of strong mixing [33, 34] continues to hold in the ensemble limit. [69.2.1.4] Therefore the same considerations as in the previous section can also be applied to the double sums (4.1) to give the finite size scaling result

P_{{X_{{MN}}}}(x)\approx H\left(x;\varpi _{X},\zeta _{X},0,DD_{{MN}}^{{\varpi _{X}}}\right) (4.2)

where now

D_{{NM}}=\left(MN\;\Lambda(MN)\right)^{{1/\varpi _{X}}} (4.3)

similar to equation (3.8).

[69.2.1.5] To exhibit the relation of the result (4.2) with the usual thermodynamic finite size scaling Ansatz (1.3) [8] for the order parameter distribution it is first necessary to rewrite the results in terms of the probability density for the ensemble averages \overline{X}_{{MN}}(\mbox{\boldmath$\vec{\varphi}$\unboldmath})=X_{{MN}}(\mbox{\boldmath$\vec{\varphi}$\unboldmath})/(MN). [69.2.1.6] This gives the thermodynamic finite size scaling result

\overline{p}_{{\overline{X}_{{MN}}}}(x)\approx\frac{(L/a)^{{d-(d/\varpi _{X})}}}{\left(\Lambda((L/a)^{d})\right)^{{1/\varpi _{X}}}}\; h\left(\frac{x\:(L/a)^{{d-(d/\varpi _{X})}}}{\left(\Lambda((L/a)^{d})\right)^{{1/\varpi _{X}}}};\varpi _{X},\zeta _{X},0,D\right). (4.4)

[69.2.1.7] Setting X=\Psi and comparing with [5] yields the identification [21, 22]

\varpi _{\Psi}=\min\left(2,\frac{\gamma _{{\Psi\Psi}}+2\beta _{\Psi}}{\gamma _{{\Psi\Psi}}+\beta _{\Psi}}\right)=\min(2,\lambda _{\Psi}) (4.5)

where \gamma _{{\Psi\Psi}} is the order parameter susceptibility exponent, \beta _{\Psi} is the order parameter exponent, and \lambda _{\Psi} is the [page 70, §0]    generalized Ehrenfest order [19] in the conjugate field direction. [70.1.0.1] The appearance of the \min-function results from the general inequality (3.7). [70.1.0.2] Similarly for the energy density X={\mathcal{E}} the result

\varpi _{{\mathcal{E}}}=\min(2,2-\alpha _{{\mathcal{E}}})=\min(2,\lambda _{{\mathcal{E}}}) (4.6)

is obtained with \alpha _{{\mathcal{E}}}=\alpha the specific heat exponent. [70.1.0.3] In general the identification is given as \varpi _{X}=\linebreak\min(2,2-\alpha _{X})=\min(2,\lambda _{X}) where \alpha _{X} is the thermodynamic fluctuation exponent [9] defined in terms of derivatives of the free energy. [70.1.0.4] Equation (4.4) in combination with equations (4.5) and (3.16) determines the thermodynamic finite size scaling function for the order parameter distribution in (1.3) explicitly as

\widetilde{p}_{\Psi}(x,y)=\left\{\begin{array}[]{rl}R(x,y)\, h_{\Psi}(x)+H_{\Psi}(x)\dfrac{\displaystyle\partial R(x,y)}{\displaystyle\partial x}&\text{\ \ \ \ :\ \ \ \ for\ \ }x\leq 0\\ &\\ R(x,y)\, h_{\Psi}(x)-\left(1-H_{\Psi}(x)\right)\dfrac{\displaystyle\partial R(x,y)}{\displaystyle\partial x}&\text{\ \ \ \ :\ \ \ \ for\ \ }x>0\end{array}\right. (4.7)

where

h_{\Psi}(x,y)=h\left(x;\frac{\gamma _{{\Psi\Psi}}+2\beta _{\Psi}}{\gamma _{{\Psi\Psi}}+\beta _{\Psi}},\zeta _{\Psi},0,D\right)=\frac{dH_{\Psi}(x)}{dx} (4.8)

and h is defined through the H-functions in equations (3.12), (3.13) and the appendix. [70.1.0.5] Note that the thermodynamic finite size scaling function depends on y only through the nonuniversal cutoff function R(x;M,y,c). [70.1.0.6] It will be seen below that the dependence on y in the universal function h reappears in fieldtheoretical finite size scaling. [70.1.0.7] Note also that the general inequalities \beta _{\Psi}>0 and \gamma _{{\Psi\Psi}}>0 imply \varpi _{\Psi}<2.

IV.B Fieldtheoretical finite size scaling

[70.1.1.1] The fieldtheoretical or statistical mechanical method of reintroducing the microscopic cell variables uses the same uncorrelated block sums as in finite ensemble scaling (3.2), but multiplies them with the M-dependent field theoretic renormalization factor for block sums D(M)/M from (2.17) which has to be calculated independently. [70.1.1.2] In this case the renormalized ensemble sums are defined as

Z_{{MN}}(\mbox{\boldmath$\vec{\varphi}$\unboldmath})=\frac{(D(M)/M)Y_{{MN}}(\mbox{\boldmath$\vec{\varphi}$\unboldmath})-C_{N}}{D_{N}}=\frac{(D(M)/M)\sum _{{j=1}}^{{N}}Y_{{MN}}(\mbox{\boldmath$\vec{\varphi}$\unboldmath}(\mbox{\boldmath$\vec{y}$\unboldmath}_{j}))-C_{N}}{D_{N}} (4.9)

where C_{N} and D_{N} are constants as in (3.2). [70.1.1.3] The composite operators Y_{{MN}}(\mbox{\boldmath$\vec{\varphi}$\unboldmath}(\mbox{\boldmath$\vec{y}$\unboldmath}_{j})) have been denoted differently from the the thermodynamic case to indicate that the variables of interest in mesoscopic fieldtheoretic or statistical mechanical calculations (block level) may in general differ from those accessible to macroscopic thermodynamic experiments (ensemble level). [70.2.0.1] Particular examples are the staggered magnetization for antiferromagnets or the quantum mechanical wave function. [70.2.0.2] Applying the same limit theorem as in the previous section now gives the fieldtheoretic finite size scaling result

P_{{Y_{{MN}}}}(x)\approx H\left(x;\varpi _{Y},\zeta _{Y},0,D^{\prime}\left(\frac{MD_{N}}{D(M)}\right)^{{\varpi _{Y}}}\right) (4.10)

for the limiting probability distribution function of ensemble sums in the ensemble limit. [70.2.0.3] Using (2.13) and going over to averages the finite size scaling form for the probability density of ensemble averages is found as

\overline{p}_{{\overline{Y}_{{MN}}}}(x)\approx\left(\frac{L}{a}\right)^{{d_{Y}}}h\left(x\:\left(\frac{L}{a}\right)^{{d_{Y}}};\varpi _{Y},\zeta _{Y},0,D^{\prime}\left(\frac{L}{\xi}\right)^{{d-\varpi _{Y}(d-d_{Y})}}\Lambda\left(\frac{L}{\xi}\right)\right) (4.11)

which is exactly of the form (1.3) with d^{*}=0. [70.2.0.4] Thus the validity of (2.13), which has to be established by independent calculation, implies the validity of hyperscaling. [70.2.0.5] Note that the fieldtheoretic finite size scaling result (4.11) appears to be different from the thermodynamic one (4.4) in that it depends on L/\xi. [70.2.0.6] It will be seen below however that the two forms are generally identical except for \varpi _{X}=2.

IV.C Hyperscaling and the Structure of the Gaussian Fixed Point

[70.2.1.1] To establish the connection between thermodynamic fluctuation exponents \varpi _{X} and fieldtheoretic correlation exponents \varpi _{Y} it is necessary to compare the scaling results (4.4) and (4.11). [70.2.1.2] Note that (4.4) holds generally by virtue of the ensemble limit while the validity of (4.11) depends upon the validity of (2.13). [70.2.1.3] The connection between thermodynamics and statistical mechanics is generally given by identifying-\log{\mathcal{Z}} with the free energy or, in the microcanonical ensemble, by inverting the logarithm of the density of states to give the internal energy as function of entropy. [70.2.1.4] Thus the identification rests upon the identification of microscopic and macroscopic energies. [70.2.1.5] In fact the energy is the only observable which will always exist microscopically and macroscopically for thermal systems because it is a defining property of the system, and generates the thermal fluctuations of interest. [70.2.1.6] Thus the connection between thermodynamics and statistical mechanics in the present probabilistic approach is provided by identifying equation (4.4) for X={\mathfrak{H}} with equation (4.11) for Y={\mathcal{H}}. [70.2.1.7] This yields the algebraic form

D(M)=M^{{1-(1/\varpi _{{\mathcal{E}}})}}\left(\frac{D^{\prime}\Lambda(N)}{D\Lambda(MN)}\right)^{{1/\varpi _{{\mathcal{E}}}}} (4.12)

for the energy renormalization. [70.2.1.8] Comparison with (2.13) and (4.6) gives the identification (first obtained in [21, 22]) [page 71, §0]

\varpi _{{\mathcal{E}}}=\min\left(2,\frac{d}{d-d_{{\mathcal{E}}}}\right)=\min(2,d\nu)=\min(2,2-\alpha) (4.13)

where \nu=\nu _{{\mathcal{E}}} is the correlation length exponent, and \alpha=\alpha _{{\mathcal{E}}} is the specific heat exponent. [71.1.0.1] Thus equation (4.12) and (4.13) combined with the general relation [9]

\frac{2-\alpha _{X}}{\nu _{X}}=\frac{2-\alpha _{Y}}{\nu _{Y}} (4.14)

establish the general validity of hyperscaling for all microscopically and macroscopically accessible observables whenever the specific heat exponent is positive. [71.1.0.2] Therefore the hyperscaling relation

\varpi _{X}=\min\left(2,\frac{d}{d-d_{X}}\right)=\min(2,d\nu _{X})=\min(2,2-\alpha _{X}) (4.15)

holds for all phase transitions with \alpha>0. [71.1.0.3] This result is a direct consequence of identifying thermal fluctuations in thermodynamics with those in statistical mechanics or field theory.

[71.1.1.1] The violation of hyperscaling above four dimensions in field theory is now a simple consequence of the renormalization group eigenvalues y_{{\mathcal{E}}}=1/\nu _{{\mathcal{E}}}=2 and y_{\Psi}=1/\nu _{\Psi}=(d+2)/2 for the Gaussian fixed point. [71.1.1.2] Equation (4.13) implies \varpi _{{\mathcal{E}}}=2 at d=4.

[71.1.2.1] Of course the present theory does not allow to conclude that hyperscaling is generally violated for \alpha\leq 0. [71.1.2.2] In fact very often hyperscaling continues to be valid in such cases. [71.1.2.3] To see how this is possible it is instructive to consider the domains of attraction for the stable laws appearing in the finite size and finite ensemble scaling formulas. [71.1.2.4] Within the present approach the fact that only stable distributions have nonempty domains of attraction [28] is the reason for the existence of fixed points in the renormalization group picture and for universality of critical behaviour [35]. [71.1.2.5] It is well known [27, 28] that the domain of attraction is very different for gaussian and nongaussian fixed points.

[71.1.3.1] The existence of the limit distribution in (4.2) for the correlated ensemble sums implies by virtue of (2.18) and (2.19) that the limiting distribution of the correlated block sums

P_{{X_{{MN}}j}}(x)=\mbox{Prob}\{ X_{{MN}}(\mbox{\boldmath$\vec{\varphi}$\unboldmath}(\mbox{\boldmath$\vec{y}$\unboldmath}_{j}))\leq x\} (4.16)

must approach a distribution within the domain of attraction of the stable distribution (4.2) for all blocks j=1,...,N. [71.1.3.2] In order that a distribution P_{{X_{{MN}}j}}(x) belongs to the domain of attraction of the stable law with index 0<\varpi _{X}<2 and parameters \zeta _{X},D it is necessary and sufficient [28] that, as |x|\rightarrow\infty,

P_{{X_{{MN}}j}}(x)=\left\{\begin{array}[]{rl}c_{-}\Lambda(-x)(-x)^{{-\varpi _{X}}}&\text{\ \ \ \ :\ \ \ \ for\ \ }x<0\\ 1-c_{+}\Lambda(x)\; x^{{-\varpi _{X}}}&\text{\ \ \ \ :\ \ \ \ for\ \ }x>0\end{array}\right. (4.17)

where \Lambda(x) is slowly varying and the constants c_{-},c_{+}\geq 0,c_{-}+c_{+}>0 are related to the parameters \varpi _{X},\zeta _{X},D by

c_{{\pm}}=\left\{\begin{array}[]{rl}\dfrac{\textstyle D\cos(\omega _{1}\zeta _{X})}{\textstyle 2\Gamma(1-\varpi _{X})\cos(\omega _{1})}\left(1\mp\cot(\omega _{1})\tan(\omega _{1}\zeta _{X})\right)&\text{\ \ \ \ :\ \ \ \ for\ \ }0<\varpi _{x}<1\\ &\\ \dfrac{\textstyle D}{\textstyle\pi}\cos(\pi\zeta _{X}/2)\left(1\mp\cot(\omega _{1})\tan(\pi\zeta _{X}/2)\right)&\text{\ \ \ \ :\ \ \ \ for\ \ }\varpi _{X}=1\\ &\\ \dfrac{\textstyle D(1-\varpi _{X})\cos(\omega _{2}\zeta _{X})}{\textstyle 2\Gamma(2-\varpi _{X})\cos(\omega _{1})}\left(1\mp\cot(\omega _{1})\tan(\omega _{2}\zeta _{X})\right)&\text{\ \ \ \ :\ \ \ \ for\ \ }1<\varpi _{x}<2\end{array}\right. (4.18)

with \omega _{1}=\pi\varpi _{X}/2 and \omega _{2}=\pi(2-\varpi _{X})/2. [71.2.0.1] For \varpi _{X}=2 on the other hand the domain of attraction is much larger. A distribution P_{{X_{{MN}}j}}(x) belongs to the domain of attraction of the Gaussian if it has a finite variance or if, for x>0,

1-P_{{X_{{MN}}j}}(x)+P_{{X_{{MN}}j}}(-x)=x^{{-2}}\Lambda(x) (4.19)

where \Lambda(x) is slowly varying.

[71.2.1.1] Equation (4.17) implies that for \varpi _{X}<2 the generalized susceptibility which is proportional to the second moment of the renormalized block variables

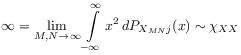\infty=\lim _{{M,N\rightarrow\infty}}\int _{{-\infty}}^{{\infty}}x^{2}\: dP_{{X_{{MN}}j}}(x)\sim\chi _{{XX}} (4.20)

diverges in each block j=1,...,N. [71.2.1.2] For \varpi _{X}=2 on the other hand the second moment may either diverge or else it is finite and nonzero. [71.2.1.3] (A zero value occurs only away from the critical point). [71.2.1.4] This result underlines the general validity of the algebraic form (2.13) derived in (4.12) for nongaussian fixed points, i.e. \varpi _{{\mathcal{E}}}<2, which then implies the validity of hyperscaling. [71.2.1.5] The Gaussian fixed point \varpi _{{\mathcal{E}}}=2 on the other hand has a much larger domain of attraction. [71.2.1.6] In particular it contains both distribution functions with algebraic tails and distributions without algebraic tails. [71.2.1.7] No general conclusion about the validity or violation of hyperscaling can be drawn in the present approach for the Gaussian fixed point.