Sie sind hier: ICP » R. Hilfer » Publikationen

II Scaling limits

[64.2.3.1] The finite size scaling limit L\rightarrow\infty,\xi\rightarrow\infty with L/\xi constant is a special kind of field theoretical scaling limit. [64.2.3.2] A fieldtheoretic scaling limit involves three different limits: 1. The thermodynamic limit L\rightarrow\infty in which the system size becomes large, 2. the continuum limit a\rightarrow 0 in which a microscopic length becomes small, and 3. the critical [page 65, §0]    limit \xi\rightarrow\infty in which the correlation length of a particular observable (scaling field) diverges.

[65.1.1.1] This section discusses the recently introduced ensemble limit [20, 21, 22, 23] as a novel kind of field theoretic scaling limit, and relates it to traditional limiting procedures.

II.A Discretization in field theory

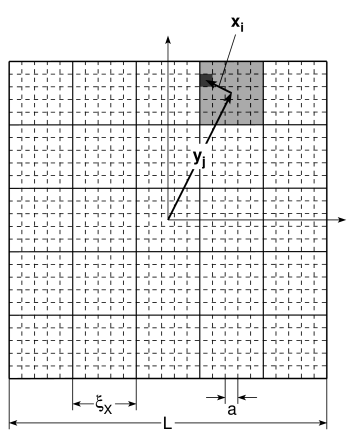
[65.1.2.1] Consider a macroscopic classical continuous system within a cubic subset of {\bf R}^{d} with volume V and linear extension L. [65.1.2.2] The finite macroscopic volume V=L^{d} is partitioned into N mesoscopic cubic blocks of linear size \xi. [65.1.2.3] The coordinate of the center of each block is denoted by \mbox{\boldmath$\vec{y}$\unboldmath}_{j}\,(j=1,...,N). [65.1.2.4] Each block is further partitioned into M microscopic cells of linear size a whose coordinates with respect to the center of the block are denoted as \mbox{\boldmath$\vec{x}$\unboldmath}_{i}\,(i=1,...,M). [65.1.2.5] The position vector for cell i in block j is \mbox{\boldmath$\vec{y}$\unboldmath}_{j}+\mbox{\boldmath$\vec{x}$\unboldmath}_{i}. [65.1.2.6] This partitioning of {\bf R}^{d} is depicted in Figure 1 for d=2 and M=N=25. [65.1.2.7] The number of blocks is given by

N=\left(\frac{L}{\xi}\right)^{d} (2.1)

while the number of cells within each block is

M=\left(\frac{\xi}{a}\right)^{d}. (2.2)

[65.2.0.1] The total number of cells inside the volume V is then NM=(L/a)^{d}.

Figure 1: Discretization of a macroscopic classical continuum system of size L into mesoscopic blocks (solid lines) of size \xi _{X} and microscopic cells (dashed lines) of size a. The vector \relax\mbox{\boldmath$\vec{y}$\unboldmath}_{j} denotes the position of block j, the vector \relax\mbox{\boldmath$\vec{x}$\unboldmath}_{i} is the position vector for cell i relative to the block center.

[65.2.0.2] Let the physical system enclosed in V be descriable as a classical field theory with timeindependent fields \mbox{\boldmath$\vec{\varphi}$\unboldmath}(\mbox{\boldmath$\vec{z}$\unboldmath},t=0)=\mbox{\boldmath$\vec{\varphi}$\unboldmath}(\mbox{\boldmath$\vec{z}$\unboldmath}) and a local microscopic configurational Hamiltonian density

\mathscr{H}(\mbox{\boldmath$\vec{\varphi}$\unboldmath})=\frac{J}{2}(\partial _{\mu}\mbox{\boldmath$\vec{\varphi}$\unboldmath}(\mbox{\boldmath$\vec{z}$\unboldmath}))^{2}+U(\mbox{\boldmath$\vec{\varphi}$\unboldmath}(\mbox{\boldmath$\vec{z}$\unboldmath})) (2.3)

where \partial _{\mu}=\partial/\partial x_{\mu}\,(\mu=1,...,d) denotes partial derivatives. [65.2.0.3] A particular example for the potential U(\mbox{\boldmath$\vec{\varphi}$\unboldmath}) would be the \phi^{4}-model for which

U(\mbox{\boldmath$\vec{\varphi}$\unboldmath})=m^{2}(\mbox{\boldmath$\vec{\varphi}$\unboldmath}(\mbox{\boldmath$\vec{z}$\unboldmath}))^{2}/2+g(\mbox{\boldmath$\vec{\varphi}$\unboldmath}(\mbox{\boldmath$\vec{z}$\unboldmath}))^{4}\,/4!. (2.4)

where the parameters m and g are the mass and the coupling constant. [65.2.0.4] For future convenience the parameters of the field theory are collected into the parameter vector \mbox{\boldmath$\vec{\Pi}$\unboldmath}=(\Pi _{1},\Pi _{2},...)=(J,m,g,...). [65.2.0.5] The partitioning introduced above allows two regularizations into a lattice field theory. [65.2.0.6] On the mesoscopic level the regularized block action representing the total configurational energy of a single block (e.g. for block j) reads

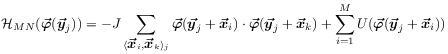{\mathcal{H}}_{{MN}}(\mbox{\boldmath$\vec{\varphi}$\unboldmath}(\mbox{\boldmath$\vec{y}$\unboldmath}_{j}))=-J\sum _{{\langle\mbox{\boldmath$\vec{x}$\unboldmath}_{i},\mbox{\boldmath$\vec{x}$\unboldmath}_{k}\rangle _{j}}}\mbox{\boldmath$\vec{\varphi}$\unboldmath}(\mbox{\boldmath$\vec{y}$\unboldmath}_{j}+\mbox{\boldmath$\vec{x}$\unboldmath}_{i})\cdot\mbox{\boldmath$\vec{\varphi}$\unboldmath}(\mbox{\boldmath$\vec{y}$\unboldmath}_{j}+\mbox{\boldmath$\vec{x}$\unboldmath}_{k})+\sum _{{i=1}}^{M}U(\mbox{\boldmath$\vec{\varphi}$\unboldmath}(\mbox{\boldmath$\vec{y}$\unboldmath}_{j}+\mbox{\boldmath$\vec{x}$\unboldmath}_{i})) (2.5)

where \langle\mbox{\boldmath$\vec{x}$\unboldmath}_{i},\mbox{\boldmath$\vec{x}$\unboldmath}_{k}\rangle _{j} denotes nearest neighbour pairs of cells inside block j,(j=1,...,N) such that each pair is counted once. [65.2.0.7] On the macroscopic level one has the discretized action between blocks (representing the total configurational energy)

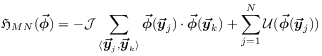{\mathfrak{H}}_{{MN}}(\mbox{\boldmath$\vec{\phi}$\unboldmath})=-\mathcal{J}\sum _{{\langle\mbox{\boldmath$\vec{y}$\unboldmath}_{j},\mbox{\boldmath$\vec{y}$\unboldmath}_{k}\rangle}}\mbox{\boldmath$\vec{\phi}$\unboldmath}(\mbox{\boldmath$\vec{y}$\unboldmath}_{j})\cdot\mbox{\boldmath$\vec{\phi}$\unboldmath}(\mbox{\boldmath$\vec{y}$\unboldmath}_{k})+\sum _{{j=1}}^{N}\mathcal{U}(\mbox{\boldmath$\vec{\phi}$\unboldmath}(\mbox{\boldmath$\vec{y}$\unboldmath}_{j})) (2.6)

where now \langle\mbox{\boldmath$\vec{y}$\unboldmath}_{j},\mbox{\boldmath$\vec{y}$\unboldmath}_{k}\rangle denotes nearest neighbour blocks. [65.2.0.8] Although the overall form of the discretizations is identical for {\mathcal{H}}_{{MN}} and {\mathfrak{H}}_{{MN}} the macroscopic discretized fields \vec{\phi} and interactions \mathfrak{J},\mathfrak{U} may in general require renormalization in the infinite volume and continuum limit, and are therefore denoted by different symbols. [65.2.0.9] Rearranging eq. (2.5) the macroscopic discretized action {\mathfrak{H}}_{{MN}}(\mbox{\boldmath$\vec{\phi}$\unboldmath}) is related to the mesoscopic discretized action {\mathcal{H}}_{{MN}}(\mbox{\boldmath$\vec{\varphi}$\unboldmath}(\mbox{\boldmath$\vec{y}$\unboldmath}_{j})) through

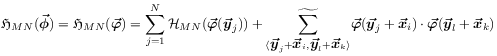{\mathfrak{H}}_{{MN}}(\mbox{\boldmath$\vec{\phi}$\unboldmath})={\mathfrak{H}}_{{MN}}(\mbox{\boldmath$\vec{\varphi}$\unboldmath})=\sum _{{j=1}}^{N}{\mathcal{H}}_{{MN}}(\mbox{\boldmath$\vec{\varphi}$\unboldmath}(\mbox{\boldmath$\vec{y}$\unboldmath}_{j}))+\underset{\langle\mbox{\boldmath$\vec{y}$\unboldmath}_{j}+\mbox{\boldmath$\vec{x}$\unboldmath}_{i},\mbox{\boldmath$\vec{y}$\unboldmath}_{l}+\mbox{\boldmath$\vec{x}$\unboldmath}_{k}\rangle}{\widetilde{\sum}}\mbox{\boldmath$\vec{\varphi}$\unboldmath}(\mbox{\boldmath$\vec{y}$\unboldmath}_{j}+\mbox{\boldmath$\vec{x}$\unboldmath}_{i})\cdot\mbox{\boldmath$\vec{\varphi}$\unboldmath}(\mbox{\boldmath$\vec{y}$\unboldmath}_{l}+\mbox{\boldmath$\vec{x}$\unboldmath}_{k}) (2.7)

expressing a decomposition into bulk plus surface energies. [65.2.0.10] Here \widetilde{\sum} expresses a summation over nearest neighbour [page 66, §0]    cells in the surface layers of adjacent blocks such that each pair of adjacent block surface cells is counted once. [66.1.0.1] Conventional field theory or equilibrium statistical mechanics assumes that the surface term which is of order {\mathcal{O}}(NM^{{(d-1)/d}}) becomes negligible compared to the bulk term which is of order {\mathcal{O}}(NM) in the field-theoretic continuum limit.

II.B Fieldtheoretic scaling limit

[66.1.1.1] Consider now a scalar local observableX_{{MN}}(\mbox{\boldmath$\vec{\varphi}$\unboldmath}(\mbox{\boldmath$\vec{x}$\unboldmath}_{i}+\mbox{\boldmath$\vec{y}$\unboldmath}_{j})) (composite operator) fluctuating from cell to cell. [66.1.1.2] The fluctuations generally define a correlation length \xi _{X}(\mbox{\boldmath$\vec{\Pi}$\unboldmath}) whose magnitude depends on the observable in question and the parameters \vec{\Pi} in the Hamiltonian. [66.1.1.3] The reconstruction of the continuum theory from its discretization is usually carried out in two steps [24]. [66.1.1.4] First one takes the (thermodynamic) infinite volume limit L\rightarrow\infty at constant a as the limit of canonical (Boltzmann-Gibbs) probability measures in the finite volume. [66.1.1.5] The existence of this limit requires stability and temperedness of the interaction potentials [25]. The limit amounts to setting N=1 and thus {\mathfrak{H}}_{{M1}}={\mathcal{H}}_{{M1}}.

[66.1.2.1] Given the existence of the infinite volume limit one studies the scaling limit a\rightarrow 0,\mbox{\boldmath$\vec{\Pi}$\unboldmath}\rightarrow\mbox{\boldmath$\vec{\Pi}$\unboldmath}_{c} of the regularized infinite-volume theory. [66.1.2.2] This field theoretic limit in general requires the renormalization of the action {\mathcal{H}}_{{M1}}(\mbox{\boldmath$\vec{\varphi}$\unboldmath}). [66.1.2.3] The quantities of main interest are the correlation functions

\displaystyle\langle X_{{\infty 1}}(\mbox{\boldmath$\vec{x}$\unboldmath}_{1})...X_{{\infty 1}}(\mbox{\boldmath$\vec{x}$\unboldmath}_{n})\rangle _{{\mbox{\boldmath$\scriptstyle\vec{\Pi}$\unboldmath}}} \displaystyle={\mathcal{Z}}^{{-1}}\;\int X_{{\infty 1}}(\mbox{\boldmath$\vec{\varphi}$\unboldmath}(\mbox{\boldmath$\vec{x}$\unboldmath}_{1}))...X_{{\infty 1}}(\mbox{\boldmath$\vec{\varphi}$\unboldmath}(\mbox{\boldmath$\vec{x}$\unboldmath}_{n}))\exp(-{\mathcal{H}}_{{\infty 1}}(\mbox{\boldmath$\vec{\varphi}$\unboldmath}(\vec{0}))){\mathcal{D}}[\mbox{\boldmath$\vec{\varphi}$\unboldmath}] (2.8)
\displaystyle=\lim _{{a\rightarrow 0}}\lim _{{L\rightarrow\infty}}\int X_{{M1}}(\mbox{\boldmath$\vec{\varphi}$\unboldmath}(\mbox{\boldmath$\vec{x}$\unboldmath}_{1}))...X_{{M1}}(\mbox{\boldmath$\vec{\varphi}$\unboldmath}(\mbox{\boldmath$\vec{x}$\unboldmath}_{n}))\; d\mu(\mbox{\boldmath$\vec{\varphi}$\unboldmath};a,L,\mbox{\boldmath$\vec{\Pi}$\unboldmath}) (2.9)

within a single block here chosen to be the one at the origin, i.e. \mbox{\boldmath$\vec{y}$\unboldmath}_{1}=\vec{0}. [66.1.2.4] The normalization constant {\mathcal{Z}} is the partition function, the measure \mu(\mbox{\boldmath$\vec{\varphi}$\unboldmath};a,L,\mbox{\boldmath$\vec{\Pi}$\unboldmath}) is the finite volume lattice probability distribution on the space of field configurations, and the notation \langle...\rangle _{{\mbox{\boldmath$\scriptstyle\vec{\Pi}$\unboldmath}}} for the expectation value expresses its dependence on the parameters in the Hamiltonian. [66.1.2.5] The correlation functions (2.9) are plagued the well known short distance singularities in the continuum limit a\rightarrow 0. [66.1.2.6] The standard approach [24] to this problem is to keep a>0 fixed and to use instead a lattice rescaling procedure in which the auxiliary rescaling factor b\propto a^{{-1}}\rightarrow\infty diverges. [66.1.2.7] This keeps the theory explicitly finite at all steps. [66.1.2.8] Thus the field theoretic continuum theory is defined through the limiting renormalized correlation functions

\langle X_{{\infty 1}}(\mbox{\boldmath$\vec{x}$\unboldmath}_{1})...X_{{\infty 1}}(\mbox{\boldmath$\vec{x}$\unboldmath}_{n})\rangle _{{\mbox{\boldmath$\scriptstyle\vec{\Pi}$\unboldmath}_{c}}}=\lim _{{b\rightarrow\infty}}A(b)^{n}\langle X_{{\infty 1}}(b\mbox{\boldmath$\vec{x}$\unboldmath}_{1})...X_{{\infty 1}}(b\mbox{\boldmath$\vec{x}$\unboldmath}_{n})\rangle _{{\mbox{\boldmath$\scriptstyle\vec{\Pi}$\unboldmath}(b)}} (2.10)

where A(b) is the field renormalization. [66.1.2.9] The parameters \vec{\Pi} approach a critical point \mbox{\boldmath$\vec{\Pi}$\unboldmath}_{c}=\mbox{\boldmath$\vec{\Pi}$\unboldmath}(\infty) such that the rescaled correlation length

\lim _{{b\rightarrow\infty}}\xi _{X}(\mbox{\boldmath$\vec{\Pi}$\unboldmath}(b))/b>0 (2.11)

remains nonzero. [66.2.0.1] The field theoretical continuum or scaling limit is called “massive” or “massless” depending on whether the rescaled correlation length approaches a finite constant or diverges to infinity. [66.2.0.2] Because a>0 is fixed equations (2.2) and (2.11) imply b\propto\xi\propto M^{{1/d}} in the massive scaling limit, and this allows to rewrite equation (2.10) as

\langle X_{{\infty 1}}(\mbox{\boldmath$\vec{x}$\unboldmath}_{1})...X_{{\infty 1}}(\mbox{\boldmath$\vec{x}$\unboldmath}_{n})\rangle _{{\mbox{\boldmath$\scriptstyle\vec{\Pi}$\unboldmath}_{c}}}=\lim _{{M\rightarrow\infty}}D(M)^{n}\langle X_{{\infty 1}}(M^{{1/d}}\mbox{\boldmath$\vec{x}$\unboldmath}_{1})...X_{{\infty 1}}(M^{{1/d}}\mbox{\boldmath$\vec{x}$\unboldmath}_{n})\rangle _{{\mbox{\boldmath$\scriptstyle\vec{\Pi}$\unboldmath}(M^{{1/d}})}} (2.12)

if the limit exists. [66.2.0.3] In that case the renormalization factor D(M) has the form

D(M)\sim M^{{d_{X}/d}} (2.13)

by virtue of the relation

A(b)\sim b^{{d_{X}}}, (2.14)

which follows generally from renormalization group theory [26]. [66.2.0.4] Here d_{X} is the anomalous dimension of the operator X.

II.C Ensemble limit

[66.2.1.1] The ensemble limit introduced in [20] is a way of defining infinite volume continuum averages from the discretized theory in a finite volume without actually calculating the measure \mu(\mbox{\boldmath$\vec{\varphi}$\unboldmath},0,\infty,\mbox{\boldmath$\vec{\Pi}$\unboldmath}_{c}) explicitly. [66.2.1.2] The idea is to focus on the one point functions given by (2.12) with n=1 as

\displaystyle\langle X_{{\infty 1}}\rangle _{{\mbox{\boldmath$\scriptstyle\vec{\Pi}$\unboldmath}_{c}}} \displaystyle=\langle X_{{\infty 1}}(\mbox{\boldmath$\vec{x}$\unboldmath}_{i})\rangle _{{\mbox{\boldmath$\scriptstyle\vec{\Pi}$\unboldmath}_{c}}} (2.15)
\displaystyle=\lim _{{M\rightarrow\infty}}D(M)\langle X_{{\infty 1}}(M^{{1/d}}\mbox{\boldmath$\vec{x}$\unboldmath}_{i})\rangle _{{\mbox{\boldmath$\scriptstyle\vec{\Pi}$\unboldmath}(M)}} (2.16)
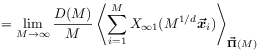\displaystyle=\lim _{{M\rightarrow\infty}}\frac{D(M)}{M}\left\langle\sum _{{i=1}}^{{M}}X_{{\infty 1}}(M^{{1/d}}\mbox{\boldmath$\vec{x}$\unboldmath}_{i})\right\rangle _{{\mbox{\boldmath$\scriptstyle\vec{\Pi}$\unboldmath}(M)}} (2.17)

where independence of \mbox{\boldmath$\vec{x}$\unboldmath}_{i} by virtue of translation invariance has been used in the first and the last equality. [66.2.1.3] At criticality these functions contain information about fluctuations through the renormalization factor D(M) for field averages.

[66.2.2.1] For a given field configuration the fluctuating local observable inside cell i\,(i=1,...,M) of block j\,(j=1,...,n) will again be denoted by X_{{MN}}(\mbox{\boldmath$\vec{\varphi}$\unboldmath}(\mbox{\boldmath$\vec{y}$\unboldmath}_{j}+\mbox{\boldmath$\vec{x}$\unboldmath}_{i})) as defined above and illustrated in Figure 1. [66.2.2.2] The block variables

X_{{MN}}(\mbox{\boldmath$\vec{\varphi}$\unboldmath}(\mbox{\boldmath$\vec{y}$\unboldmath}_{j}))=\sum _{{i=1}}^{{M}}X_{{MN}}(\mbox{\boldmath$\vec{\varphi}$\unboldmath}(\mbox{\boldmath$\vec{y}$\unboldmath}_{j}+\mbox{\boldmath$\vec{x}$\unboldmath}_{i})) (2.18)

(j=1,...,N) are defined by summing the cell variables and the ensemble variable [page 67, §0]

X_{{MN}}(\mbox{\boldmath$\vec{\varphi}$\unboldmath})=\sum _{{j=1}}^{{N}}X_{{MN}}(\mbox{\boldmath$\vec{\varphi}$\unboldmath}(\mbox{\boldmath$\vec{y}$\unboldmath}_{j})) (2.19)

is obtained by summing the block variables. For a>0 the ensemble limit is defined as the limit

M\rightarrow\infty,N\rightarrow\infty,\frac{N}{M}=\frac{aL}{\xi _{X}(\mbox{\boldmath$\vec{\Pi}$\unboldmath})^{2}}=C_{0} (2.20)

where C_{0} is a constant. [67.1.0.1] In the ensemble limit L\sim(\xi _{X}(\mbox{\boldmath$\vec{\Pi}$\unboldmath}))^{2} as compared to L\sim\xi _{X}(\mbox{\boldmath$\vec{\Pi}$\unboldmath}) in the fieldtheoretic scaling limit. [67.1.0.2] The difference to the field theoretic scaling limit is that thermodynamic (L\rightarrow\infty), continuum (a\rightarrow 0) and critical (\mbox{\boldmath$\vec{\Pi}$\unboldmath}\rightarrow\mbox{\boldmath$\vec{\Pi}$\unboldmath}_{c}) limit are taken simultaneously. [67.1.0.3] In this way an infinite ensemble of regularized infinite classical continuum systems is generated. [67.1.0.4] The elements of the ensemble are replicas of one and the same system governed by the Hamiltonian density \mathscr{H}(\mbox{\boldmath$\vec{\varphi}$\unboldmath}). [67.1.0.5] Thus the ensemble limit generates an ensemble in the sense of statistical mechanics.

[67.1.1.1] The critical or noncritical averages \langle X_{{\infty 1}}\rangle _{{\mbox{\boldmath$\scriptstyle\vec{\Pi}$\unboldmath}}} can be calculated in the ensemble limit as

\langle X_{{\infty 1}}\rangle _{{\mbox{\boldmath$\scriptstyle\vec{\Pi}$\unboldmath}}}=\lim _{{M,N\rightarrow\infty}}\frac{1}{MN}X_{{MN}}(\mbox{\boldmath$\vec{\varphi}$\unboldmath}). (2.21)

[67.1.1.2] This equation states that macroscopic ensemble averages can either be calculated using equations (2.9) in the traditional scaling limit or directly using equations (2.18) and (2.19) in the ensemble limit. [67.1.1.3] Equation (2.21) gives the connection between the scaling limit and the ensemble limit. [67.1.1.4] Note that the validity of eq. (2.21) requires the existence of the renormalized field theory. [67.1.1.5] Thus the left hand side of (2.21) cannot be calculated at anequilibrium phase transitions [21, 22] while the right hand side can still be calculated in such cases.

Table 1: Different possible scaling limits. FSS stands for finite size scaling, and ES for ensemble scaling.
Type of scaling limit a L \vec{\Pi} \frac{aL}{\xi^{2}} M N \frac{N}{M}
1. discrete ES limit \rightarrow 0 \rightarrow\infty \rightarrow\mbox{\boldmath$\vec{\Pi}$\unboldmath}_{c} \rightarrow c^{{1/d}} \rightarrow\infty \rightarrow\infty \rightarrow c
2. \rightarrow 0 \rightarrow\infty =\mbox{\boldmath$\vec{\Pi}$\unboldmath}_{c} =0 =\infty =1 =0
3. massive scaling limit \rightarrow 0 =\infty \rightarrow\mbox{\boldmath$\vec{\Pi}$\unboldmath}_{c} =\infty =\infty \rightarrow 1 =0
4. massless scaling limit \rightarrow 0 =\infty =\mbox{\boldmath$\vec{\Pi}$\unboldmath}_{c} =\frac{\infty}{\infty^{2}} =\infty =1 =0
5. massive FSS limit =0 \rightarrow\infty \rightarrow\mbox{\boldmath$\vec{\Pi}$\unboldmath}_{c} =0 =\infty \rightarrow N_{0} =0
6. massless FSS limit =0 \rightarrow\infty =\mbox{\boldmath$\vec{\Pi}$\unboldmath}_{c} =\frac{0}{\infty^{2}} =\infty =1 =0
7. continuum ES limit =0 =\infty \rightarrow\mbox{\boldmath$\vec{\Pi}$\unboldmath}_{c} =0\cdot\infty =\infty =\infty =\frac{\infty}{\infty}
8. =0 =\infty =\mbox{\boldmath$\vec{\Pi}$\unboldmath}_{c} =\frac{0\cdot\infty}{\infty^{2}} =\infty =1 =0

II.D Summary of different scaling limits

[67.1.2.1] The main difference of the ensemble limit as compared to other scaling limits is that the three limits a\rightarrow 0,L\rightarrow\infty,\mbox{\boldmath$\vec{\Pi}$\unboldmath}\rightarrow\mbox{\boldmath$\vec{\Pi}$\unboldmath}_{c} are simultaneously performed while in other limits only two of these limits are taken simultaneously. [67.1.2.2] There are 2^{3}=8 ways of performing the scaling limit with the three variables a,L,\mbox{\boldmath$\vec{\Pi}$\unboldmath} depending on whether a particular variable is set equal to its limiting value or not. [67.2.0.1] The different possibilities are summarized in Table I. [67.2.0.2] Note that only the ensemble limit (1.) and the related critical limit (7.) in an infinite continuum theory yield an infinite number of uncorrelated blocks. [67.2.0.3] The close relation between the ensemble limit and the massive finite size scaling limit (5.) is apparent if N_{0}\gg 1.