Sie sind hier: ICP » R. Hilfer » Publikationen

VII Amplitude ratios

[74.1.2.1] This section discusses universal amplitudes such as those defined in (1.6) and their ratios. [74.1.2.2] In numerical simulations of critical phenomena amplitude ratios such as (1.7) are used routinely to extract critical parameters \mbox{\boldmath$\vec{\Pi}$\unboldmath}_{c} and exponents from simulations of finite systems. [74.1.2.3] It is then of interest to analyze finite size amplitude ratios within the present framework.

[74.1.3.1] The absolute moment of order \sigma for the ensemble averages of X in a finite and noncritical system is found from equations (4.4) and (3.16) as

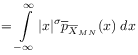\displaystyle\langle|X|^{\sigma}\rangle \displaystyle=\int _{{-\infty}}^{{\infty}}|x|^{\sigma}\overline{p}_{{\overline{X}_{{MN}}}}(x)\; dx (7.1)
\displaystyle=\frac{\left(\Lambda((L/a)^{d})\right)^{{\sigma/\varpi _{X}}}}{(L/a)^{{d\sigma(1-(1/\varpi _{X}))}}}\;\widetilde{X}(\sigma;a,\xi,L) (7.2)

where the amplitude \widetilde{X}(\sigma;a,\xi,L) of the finite, discrete and noncritical system is given as

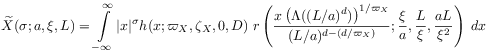\widetilde{X}(\sigma;a,\xi,L)=\int _{{-\infty}}^{{\infty}}|x|^{\sigma}h(x;\varpi _{X},\zeta _{X},0,D)\; r\left(\frac{x\left(\Lambda((L/a)^{d})\right)^{{1/\varpi _{X}}}}{(L/a)^{{d-(d/\varpi _{X})}}};\frac{\xi}{a},\frac{L}{\xi},\frac{aL}{\xi^{2}}\right)\; dx (7.3)

and the function r(x;\xi/a,L/\xi,aL/\xi^{2}) is defined from equation (4.7) by replacing \Psi with X and extracting a factor h(x;\varpi _{X},\zeta _{X},0,D). [74.2.0.1] In the ensemble limit one obtains from this and (3.17) the result

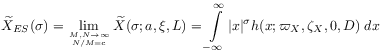\widetilde{X}_{{ES}}(\sigma)=\lim _{{\genfrac{}{}{0.0pt}{}{M,N\rightarrow\infty}{N/M=c}}}\widetilde{X}(\sigma;a,\xi,L)=\int _{{-\infty}}^{{\infty}}|x|^{\sigma}h(x;\varpi _{X},\zeta _{X},0,D)\; dx (7.4)

for the critical ensemble scaling amplitude of order \sigma in an infinite system. [74.2.0.2] The subscript is again a reminder for the ensemble scaling limit. [74.2.0.3] The integral in (7.4) can be evaluated for D=1 as

\widetilde{X}_{{ES}}(\sigma)=\frac{2}{\pi}\Gamma(\sigma)\Gamma\left(1-\frac{\sigma}{\varpi _{X}}\right)\sin(\pi\sigma/2)\cos\left(\frac{\pi\sigma\zeta _{X}(\varpi _{X}-2)}{2\varpi _{X}}\right), (7.5)

which is valid for -1<\mbox{Re}\sigma<\varpi _{X},1<\varpi _{X}<2 and -1<\zeta _{X}<1. [74.2.0.4] A derivaton of this result is given in Appendix B. [74.2.0.5] This allows to calculate the general moment ratios

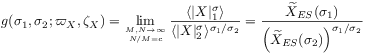g(\sigma _{1},\sigma _{2};\varpi _{X},\zeta _{X})=\lim _{{\genfrac{}{}{0.0pt}{}{M,N\rightarrow\infty}{N/M=c}}}\frac{\langle|X|^{\sigma}_{1}\rangle}{\langle|X|^{\sigma}_{2}\rangle^{{\sigma _{1}/\sigma _{2}}}}=\frac{\widetilde{X}_{{ES}}(\sigma _{1})}{\left(\widetilde{X}_{{ES}}(\sigma _{2})\right)^{{\sigma _{1}/\sigma _{2}}}} (7.6)

with -1<\sigma _{1},\sigma _{2}<\varpi _{X} in the ensemble limit. [74.2.0.6] Figure 6 shows a twodimensional plot of the ratio g(3/4,1/4;\varpi _{X},\zeta _{X}).

Figure 6: The moment ratio g(3/4,1/4;\varpi _{X},\zeta _{X})=\langle|X|^{{3/4}}\rangle/\langle|X|^{{1/4}}\rangle^{3} as a function of the critical exponent \varpi _{X} and the universal shape parameter \zeta _{X}.

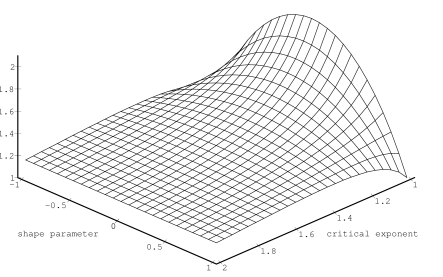
[74.2.1.1] If equation (7.5) is used to analytically continue g(\sigma _{1},\sigma _{2};\varpi _{X},\zeta _{X}) beyond the regime -1<\sigma _{1},\sigma _{2}<\varpi _{X} the traditional fourth order cumulant g(4,2;\varpi _{\Psi},\zeta _{\Psi}) for the order parameter is found to exhibit special problems if \varpi _{\Psi}<2. [74.2.1.2] This is mainly due to the presence of the factor \sin(\pi\sigma/2) in (7.5). [74.2.1.3] The divergence must somehow become absorbed by the cutoff factor r(0;\infty,c,0) in the finite size scaling limit. [74.2.1.4] Assuming that this is indeed the case it is then of interest to consider the quantity

g_{{FSS}}(\sigma _{1},\sigma _{2};\varpi _{X},\zeta _{X})=\lim _{{\genfrac{}{}{0.0pt}{}{L,\xi\rightarrow\infty}{L/\xi=c}}}\frac{\left(\sin(\pi\sigma _{2}/2)^{{\sigma _{1}/\sigma _{2}}}\langle|X|^{{\sigma _{1}}}\rangle\right)}{\sin(\pi\sigma _{1}/2)\langle|X|^{{\sigma _{2}}}\rangle^{{\sigma _{1}/\sigma _{2}}}} (7.7)

[page 75, §0]    in the finite size scaling limit assuming that it exists. [75.1.0.1] Then the traditional finite size cumulant becomes

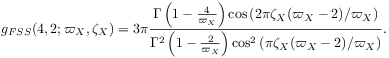g_{{FSS}}(4,2;\varpi _{X},\zeta _{X})=3\pi\frac{\Gamma\left(1-\frac{4}{\varpi _{X}}\right)\cos\left(2\pi\zeta _{X}(\varpi _{X}-2)/\varpi _{X}\right)}{\Gamma^{2}\left(1-\frac{2}{\varpi _{X}}\right)\cos^{2}\left(\pi\zeta _{X}(\varpi _{X}-2)/\varpi _{X}\right)}. (7.8)

[75.1.0.2] The interest in this formal expression is that it is still singular. [75.1.0.3] Within the domain 1<\varpi _{X}<2,-1<\zeta _{X}<1 it has simple poles along the lines

\begin{array}[]{l}\varpi _{X}=\dfrac{4}{3}\\ \varpi _{X}=\dfrac{4\zeta _{X}}{2\zeta _{X}\pm 1}\end{array} (7.9)

and zeros along the lines

\begin{array}[]{l}\varpi _{X}=\dfrac{8\zeta _{X}}{4\zeta _{X}\pm 1}\\ \varpi _{X}=\dfrac{8\zeta _{X}}{4\zeta _{X}\pm 3}.\end{array} (7.10)

[75.1.0.4] For the traditionally studied order parameter cumulant, i.e. setting X=\Psi, the pole at 4/3 implies a divergence whenever \delta=3, i.e. in mean field theory. [75.1.0.5] This result is consistent with the divergence g_{\infty}(0)\propto\eta^{{-1}} found in conformal field theory [17]. [75.1.0.6] Note that the points \zeta=\pm 1/2 along the singular mean field line \varpi _{\Psi}=4/3 are intersection points with a line of zeros.

[75.1.1.1] Irrespective of these problems it is of interest to estimate values for the traditional order parameter cumulant ratio g_{\infty}(0) because much previous work has focussed on it. [75.1.1.2] Within the present approach this is possible from the knowledge of the scaling functions if it is assumed that the identification of \zeta=1 with periodic boundary conditions holds generally. [75.1.1.3] If the scaling functions with \zeta=1 in Figures 2 through 4 are simply truncated sharply at \pm x_{{max}}, and subseqently rescaled to unit norm and variance, the order parameter cumulant g_{\infty}(0) may be calculated as usual, and it will depend upon the nonuniversal cutoff at x_{{max}}. [75.2.0.1] The results of such a cutoff procedure are displayed in Figure 7 for the cases \delta=3,5,15. [75.2.0.2] It is seen that the cumulant is distinctly cutoff dependent. [75.2.0.3] Note that all curves appear to diverge as the cutoff increases.

Figure 7: Plot of g_{\infty}(0) calculated by truncating \widetilde{p}_{\Psi}(x;\delta,1,1/2) at \pm x_{{max}} and choosing the scale factors to give unit norm and variance. Solid arrows indicate numerical estimates from Monte-Carlo simulations on Ising models as g_{\infty}(0)=1.168\pm 0.002 for d=2 Ref. [43], g_{\infty}(0)=1.59\pm 0.03 for d=3 Ref. [16] and g_{\infty}(0)=2.04\pm 0.05 for d=5 Ref. [46]. The dashed arrow represents the analytical result g_{\infty}(0)=2.188... from Ref. [15].

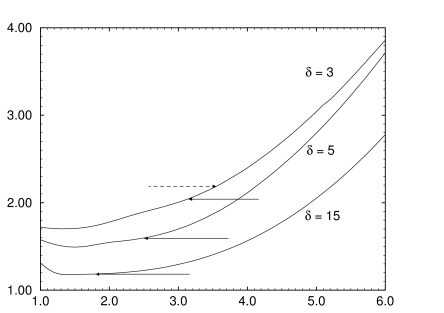
[75.2.0.4] For the cases \delta=3 and \delta=5 some structure appears between x_{{max}}=2 and 3 corresponding to the strong curvature in this region seen in Figures 2 and 3. [75.2.0.5] For the 2d-Ising case the curve is flat up to about twice the maximal value 1.39 for the simulations of Bruce and coworkers [43, 45]. [75.2.0.6] Figure 5 provides a possible explanation for the poor agreement between the value g_{\infty}(0)=2.042\pm 0.05 observed in simulations of the fivedimensional Ising model [11, 46] and the mean field calculation g_{\infty}(0)=2.188... from [15]. [75.2.0.7] The simulation result is indicated as the solid arrow, the analytical result as the dashed arrow pointing to the curve \delta=3. [75.2.0.8] The small difference in the cutoff x_{{max}} corresponding to these values suggests that the discrepancy may result from different nonuniversal (but most likely smooth) cutoffs in the two estimates.

[75.2.1.1] Finally, the fact that the value of the universal shape parameter \zeta _{X} appears to be related to the choice of bondary conditions suggests a method of constructing critical amplitude ratios which do not depend on boundary conditions, or other factors influencing \zeta _{X}. [75.2.1.2] The basic idea is to use the difference of two independent observations of ensemble averages or sums. [75.2.1.3] Let X_{{MN}} and X_{{MN}}^{\prime} be two independent measurements and Y_{{MN}}=X_{{MN}}-X_{{MN}}^{\prime} their difference. [75.2.1.4] The limiting distribution function P_{{X_{{MN}}}}(x) for X_{{MN}} and X_{{MN}}^{\prime} at criticality is given in equation (4.2). [75.2.1.5] Then the difference Y_{{MN}} has the distribution function

P_{{Y_{{MN}}}}(x)\approx H\left(x;\varpi _{X},0,0,2DD_{{MN}}^{{\varpi _{X}}}\right) (7.11)

[page 76, §0]    in which the width is doubled, but \zeta _{X} has disappeared. [76.1.0.1] The fractional difference moment ratio \Delta(\sigma _{1},\sigma _{2},\varpi _{X}) is formed analogously to the moment ratio g as

\Delta(\sigma _{1},\sigma _{2},\varpi _{X})=\frac{\langle|Y_{{MN}}|^{{\sigma _{1}}}\rangle}{\langle|Y_{{MN}}|^{{\sigma _{2}}}\rangle^{{\sigma _{1}/\sigma _{2}}}}=\frac{(2/\pi)\Gamma(1-(\sigma _{1}/\varpi _{X}))\Gamma(\sigma _{1})\sin(\pi\sigma _{1}/2)}{\left[(2/\pi)\Gamma(1-(\sigma _{2}/\varpi _{X}))\Gamma(\sigma _{2})\sin(\pi\sigma _{2}/2)\right]^{{\sigma _{1}/\sigma _{2}}}} (7.12)

and it has a universal value depending only on the scaling dimension of X as long as \sigma _{1},\sigma _{2}<\varpi _{X}. [76.1.0.2] If the scaling dimension is universal then the fractional difference moment ratio is independent of boundary conditions. [76.1.0.3] Plotting \Delta(\sigma _{1},\sigma _{2},\varpi _{X}) as a function of length scale and temperature should then allow to extract the critical exponent.